Стадии шизофрении у мужчин
Первые признаки шизофрении у мужчин: поведение
Шизофрения – психическое расстройство, имеющее загадочную природу. Исследователи до сих пор имеют трудности с ответом на вопрос касаемо причины...
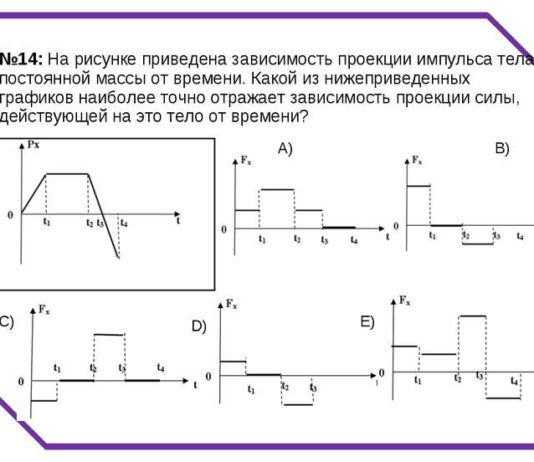
Проекция импульса тела
§ 20. Импульс тела. Закон сохранения импульса
Законы Ньютона позволяют решать различные практически важные задачи, касающиеся взаимодействия и движения тел. Большое число таких задач связано,...
Стрессоустойчивость как сохранять спокойствие
Стрессоустойчивость. Как сохранять спокойствие и эффективность в любых ситуациях
Все права защищены. Никакая часть настоящего издания ни в каких целях не может быть воспроизведена в...
Советы
Муж ушел к старой
15 поводов улыбнуться, когда муж ушел к молодой
Ты постоянно рисуешь ненавистные картинки того, как ему хорошо с другой? Рыдаешь в подушку и худеешь на...
Лучшие
Комментарии
Главное не грусти
Главное, ты не грусти.
Грусть проникает под кожу и болью солёной Льётся из глаз, заставляя надежды крушить. Жжёт изнутри, будто съела полсотни лимонов… Я без...
От других психологов
Как вести себя в женском коллективе?
Мы выяснили, как выжить в чисто женском коллективе, избежать закулисных сплетен и стать всеобщей любимицей.Милые улыбчивые коллеги, готовые всегда прийти на помощь, подсказать, где...
Релаксация для сна лечение
Музыка для сна слушать онлайн (йога, медитация и релаксация)
Засыпайте под легкую и спокойную музыку для сна на сайте Звуки природы. Лёгкий гипноз от прослушивания!...
Психологическое давление статья
Давление психологическое – это влияние, оказываемое одним человеком на других людей с целью изменения их мнений, решений, суждений, или личностных установок. Оно осуществляется далеко...
Человек верящий в рок
Человек, верящий в рок, 8 букв, 4 буква «А», сканворд
Слово из 8 букв, первая буква - «Ф», вторая буква - «А», третья буква -...
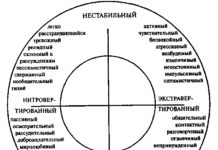
Методика айзенка по определению темперамента
Личностный опросник Айзенка EPI, вариант A
Личностный опросник EPI (Eysenck Personality Inventory) – третий вариант личностного опросника Айзенка, опубликован в 1963 году. Он также состоит...
Двумя словами
История болезни шизофренией
История болезни. Клинический диагноз: Шизофрения, простая форма, непрерывное течение, F 20.6
Страницы работы
Фрагмент текста работы
1. Паспортная часть
· Профессия, место работы: студент 5 курса БГУИР
· Домашний...