Татьяна Ефимова предлагает статью на тему: "проекция стороны на прямую" с детальным описанием.
Содержание
- 1 Как найти проекцию прямой на плоскость
- 2 Нахождение проекции точки на прямую.
- 3 Лекция 2. Ортогональные проекции прямой
- 4 Проецирование прямого угла
- 5 Задание 4. Найти проекцию точки Р(-8,12) на прямую, проходящую через точки А(2,- 3) и В(- 5.1)
- 6 Точка на прямой
- 7 геометрия – Как найти проекцию точки $%A(2;3;4)$% на прямую $%x = y = z$%?
- 8 Проецирование прямого угла на плоскость проекций
Как найти проекцию прямой на плоскость
- Как найти проекцию прямой на плоскость
- Как построить точку с тремя координатами
- Как найти проекцию точки на прямую
- – плоскость;
- – прямая, не принадлежащая данной плоскости;
- – угольник;
- – карандаш.
Чтобы лучше представить, как образуется прямоугольная проекция, проделайте следующий опыт. Повесьте на стену небольшой экран. Можно использовать и просто белую стену. Вам понадобится еще кусок веревки и 2 стула или прикрепленных к столу стойки, а также любой источник света. Привяжите веревку к стойкам. Поставьте их так, чтобы шнур был натянут и находился под углом к экрану. Измерьте шнур.
Поставьте настольную лампу так, чтобы ее луч падал на экран под прямым углом. При этом он должен освещать и веревку. Погасив верхний свет, вы увидите, что натянутый шнур отбрасывает тень на экран, и длина тени не совпадает с длиной шнура. Тень и представляет собой проекцию — в данном случае, прямоугольную. Поэкспериментируйте, размещая источник света так, чтобы его луч падал на экран под разными углами.
Нахождение проекции точки на прямую.
Вообще проецирование некоторой фигуры на прямую является обобщением понятия ортогонального проецирования фигуры на плоскость (смотрите статью проекция точки на плоскость).
Так как все геометрические фигуры состоят из точек, а проекция фигуры представляет собой множество проекций всех точек этой фигуры, то для проецирования фигуры на прямую необходимо уметь проецировать точки этой фигуры на данную прямую.
Так что же называют проекцией точки на прямую?
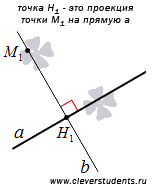
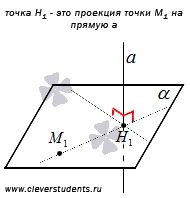
Проекция точки на прямую – это либо сама точка, если она лежит на данной прямой, либо основание перпендикуляра, опущенного из этой точки на заданную прямую.
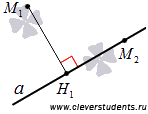
На приведенном ниже рисунке точка H1 является проекцией точки M1 на прямую a, а точка M2 есть проекция самой точки М2 на прямую a, так как М2 лежит на прямой a.
Это определение проекции точки на прямую справедливо как для случая на плоскости, так и для случая в трехмерном пространстве.
На плоскости, чтобы построить проекцию точки М1 на прямую a нужно провести прямую b, которая проходит через точку М1 и перпендикулярна прямой a. Тогда точка пересечения прямых a и b является проекцией точки М1 на прямую a.
В трехмерном пространстве проекцией точки М1 на прямую a является точка пересечения прямой a и плоскости
К началу страницы
Нахождение координат проекции точки на прямую – теория и примеры.
Начнем с нахождения координат проекции точки на прямую, когда проецируемая точка и прямая заданы в прямоугольной системе координат Oxy на плоскости. После этого покажем, как находятся координаты проекции точки на прямую в прямоугольной системе координат Oxyz в трехмерном пространстве.
Координаты проекции точки на прямую на плоскости.
Пусть на плоскости зафиксирована прямоугольная система координат Oxy, задана точка
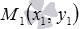
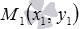
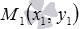
Решим эту задачу.
Проведем через точку М1 прямую b, перпендикулярную прямой a, и обозначим точку пересечения прямых a и b как H1. Тогда H1 – проекция точки М1 на прямую a.
Из проведенного построения логически следует алгоритм, позволяющий найти координаты проекции точки
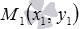
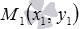
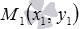
составляется уравнение прямой a, если, конечно, оно не дано сразу (это легко сделать, если Вы знаете основные уравнения прямой на плоскости);
записывается уравнение прямой b, которая проходит через точку
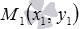
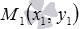
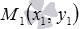
находятся требуемые координаты проекции точки М1 на прямую a как координаты точки пересечения прямых a и b – для этого решается система уравнений, составленная из уравнений прямых a и b.
Координаты проекции точки на прямую в трехмерном пространстве.
Теперь переходим к нахождению координат проекции точки на прямую относительно прямоугольной системы координат Oxyz, введенной в трехмерном пространстве.
Пусть в пространстве зафиксирована прямоугольная система координат Oxyz, задана точка
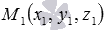
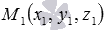
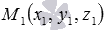
Решим эту задачу.
Построим плоскость











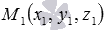
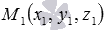
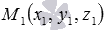
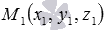
записываем уравнения прямой a, если они не заданы в условии задачи (справиться с этой задачей поможет материал статьи уравнения прямой в пространстве);
составляем уравнение плоскости





находим требуемые координаты проекции точки
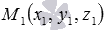
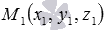
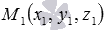






БИЛЕТ №41.
Последнее изменение этой страницы: 2016-08-16; Нарушение авторского права страницы
Лекция 2. Ортогональные проекции прямой
2.1. Задание прямой на эпюре
Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.
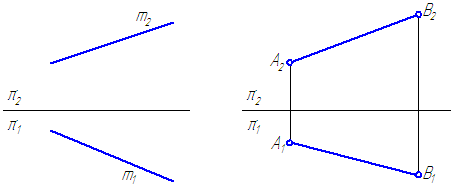
а б
Рисунок 2.1 – Проекции прямой
Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения .
Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.
2.2. Прямые частного положения
Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения .
Прямые, параллельные плоскостям проекций, называются прямыми уровня .
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).
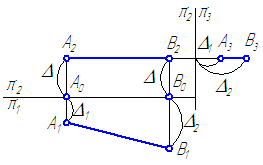
Рисунок 2.2 – Эпюр горизонтали
Если отрезок параллелен плоскости проекций π1, то его фронтальная проекция А2В2 параллельна оси проекций π1/π2, а горизонтальная проекция отрезка А1В1 определяет истинную величину АВ:
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).
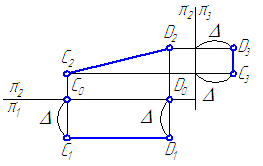
Рисунок 2.3 – Эпюр фронтали
Если отрезок параллелен плоскости проекций π2, то его горизонтальная проекция параллельна оси проекций π2/π1, а фронтальная проекция отрезка C2D2 определяет истинную величину CD.
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).
Прямые, перпендикулярные плоскостям проекций, называются проецирующими .
Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).
Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).
Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).
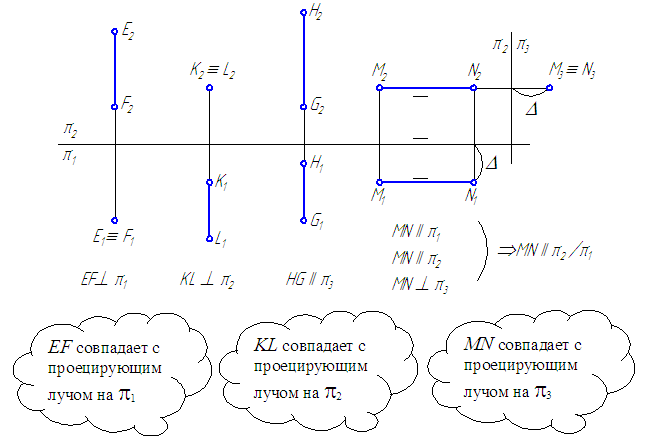
Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH
2.3. Метод прямоугольного треугольника
Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.
Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π1 (Рисунок 2.5).
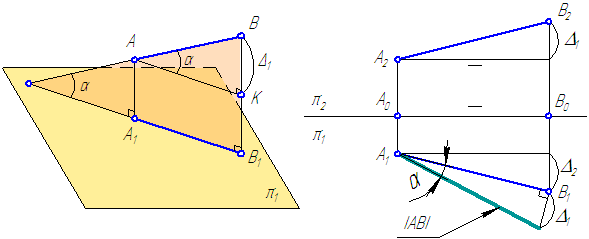
Рисунок 2.5 – Определение истинной величины отрезка общего положения
На рисунке 2.5, а:
АА1 – расстояние от точки А до плоскости проекций π1;
ВВ1 – расстояние от точки В до плоскости проекций π1;
ΔАКВ – прямоугольный треугольник, в котором:
ВК=ВВ1–АА1=Δ1 – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π1 (то есть, разности координат Z точек А и В);
АВ – гипотенуза ΔАКВ – истинная величина.
При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.
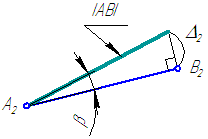
Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π2
2.4. Точка и прямая
Если точка принадлежит прямой, то её проекции:
- Принадлежат одноимённым проекциям данной прямой;
- Лежат на одной линии связи.
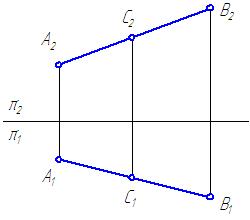
Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:
Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:
Упражнение
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)
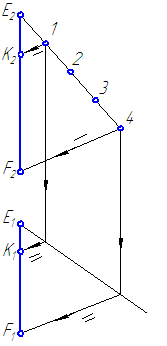
Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:
- Проведём произвольную прямую из любого конца любой проекции отрезка, например, Е2.
- Отложим на этой прямой от точки Е2 равные отрезки, количество которых равно сумме чисел, составляющих дробь (в нашем примере 1+3=4).
- Соединим последнюю точку 4 с другим концом фронтальной проекции отрезка – точкой F2.
- Из точки 1 проведём прямую, параллельную прямой (4—F2) до пересечения с проекцией E2F2, таким образом будет найдена фронтальная проекция искомой точки К2.
- Горизонтальную проекцию точки К1 получим путём построения линии проекционной связи до пересечения её с горизонтальной проекцией отрезка.
Упражнение
Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).
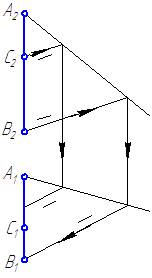
Рисунок 2.9 – Решение упражнения 2
Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.
2.5. Следы прямой
След прямой – точка пересечения прямой с плоскостью проекций.
Прямая общего положения в общем случае может быть три следа:
- горизонтальный след M1– точка пересечения прямой с горизонтальной плоскостью проекций π1;
- фронтальный след N2– точка пересечения прямой с фронтальной плоскостью проекций π2;
- профильный след L3 – точка пересечения прямой с профильной плоскостью проекций π3.
След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:
- горизонтальный след совпадает со своей горизонтальной проекцией M≡M1,
- фронтальный – с фронтальной проекцией N≡N2,
- профильный – с профильной проекцией L≡L3 (Рисунок 2.10).
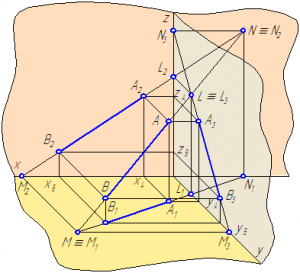
Рисунок 2.10 – Построение следов отрезка прямой АВ
Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).
Для построения горизонтального следа прямой АB необходимо:
- Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
- Из точки М2 восстановить перпендикуляр (линию проекционной связи) до его пересечения с горизонтальной проекцией прямой АBили её продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.
Чтобы построить фронтальный след отрезка АB прямой, необходимо:
- Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
- Из точки N1 восстановить перпендикуляр (линию проекционной связи) до его пересечения с фронтальной проекцией прямой АB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Ниже приводим алгоритм построения следов отрезка прямой АВ:
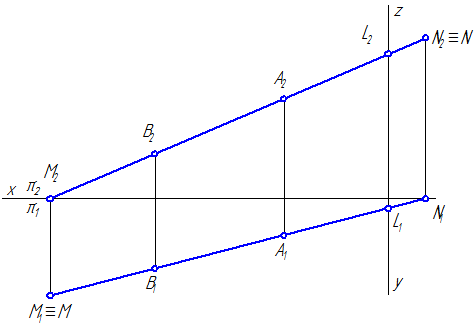
Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ
Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.
2.6. Взаимное расположение прямых
Две прямые в пространстве могут быть:
- параллельными;
- пересекающимися;
- скрещивающимися.
Параллельные прямые – прямые, пересекающиеся в несобственной точке.
Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).
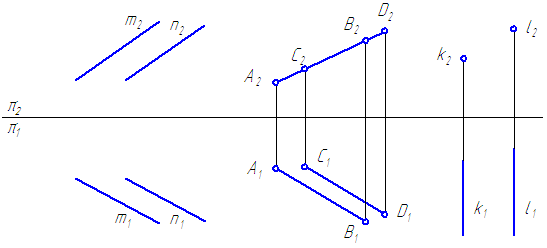
Рисунок 2.12 – Параллельные прямые
Пересекающиеся прямые – прямые, имеющие одну общую точку.
Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).
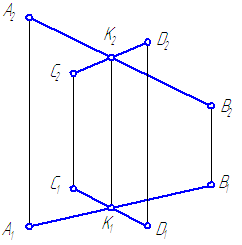
Рисунок 2.13 – Пересекающиеся прямые
Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).
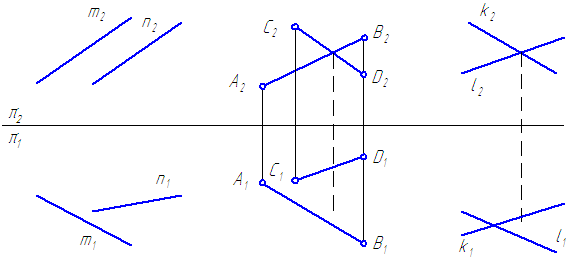
Рисунок 2.14 — Скрещивающиеся прямые
2.7. Проекции плоских углов
Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.
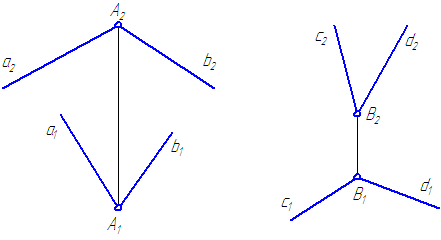
Рисунок 2.15
По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.
Теорема о проецировании прямого угла в частном случае
Теорема . Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла (Рисунок 2.16, а и б).
Обратная теорема . Если одна из двух пересекающихся прямых параллельна некоторой плоскости проекций и проекции этих прямых на эту же плоскость пересекаются под прямым углом, то в пространстве эти прямые взаимно перпендикулярны.
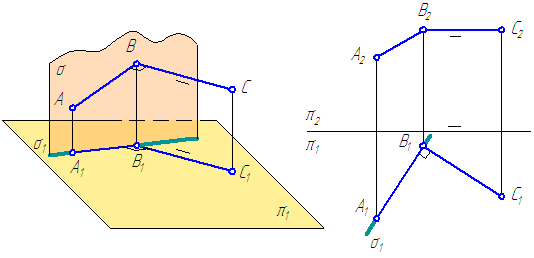
а б
Рисунок 2.16 – Проецирование прямого угла
Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,
2.8. Задачи для самостоятельного решения
1. Построить отрезок прямой АВ // π1, равный 35 мм и наклонённый к π2 под углом 25° (Рисунок 2.17).
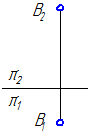
Рисунок 2.17
2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π2 и π1.
3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π1 и 45° — к плоскости проекций π2.
4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π2/π1 (Рисунок 2.18).
Проецирование прямого угла
При пересечении двух прямых образуются углы, которые проецируются на любую плоскость проекций без искажений в случае, если обе прямые лежат в плоскости, параллельной плоскости проекций. Если две прямые пересекаются под прямым углом, то следует знать, что проецирование прямого угла имеет особое свойство.
Если одна из сторон прямого угла параллельна одной из плоскостей проекций, то прямой угол проецируется на эту плоскость без искажений (инвариантные свойства параллельного проецирования).
На комплексном чертеже (рисунок 14 а, б, в) показаны проекции взаимно перпендикулярных прямых, где а, б, с – прямые общего положения; h – горизонталь, f – фронталь, р – профильная прямая уровня.
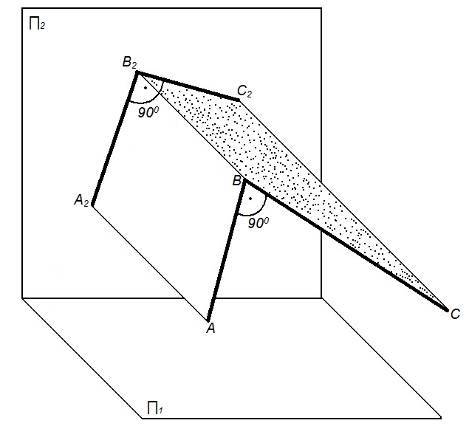
Рисунок 13 – Проецирование прямого угла
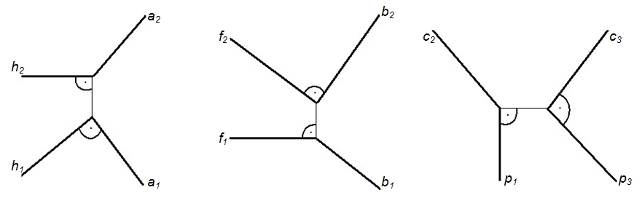
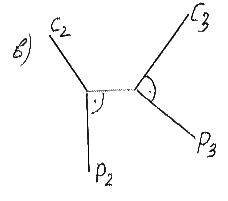

Рисунок 14 – Комплексный чертеж взаимно перпендикулярных прямых
Плоскость
Проекцией любой плоскости является геометрическое место проекций всех ее точек. Если рассматривать плоскость, расположенную не перпендикулярно и не параллельно ни одной из плоскостей проекций, то ее проекции целиком заполнят собой поля плоскостей П1, П2, П3. Поэтому на комплексном чертеже задаются лишь некоторые геометрические элементы, определяющее положение заданной плоскости в пространстве (таблица 1):.
Таблица 1 – Способы задания плоскости
| Задание плоскости | Наглядное изображение | Комплексный чертеж |
| Тремя точками, не лежащими на одной прямой | 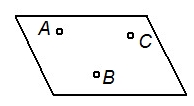  |
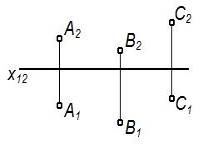  |
| Прямой и точкой, не принадлежащей прямой | 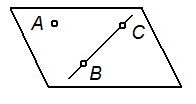  |
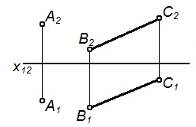  |
| Двумя параллельными прямыми | 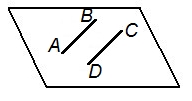  |
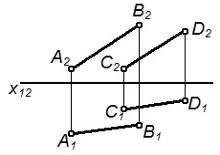  |
| Двумя пересекающимися прямыми | 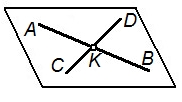  |
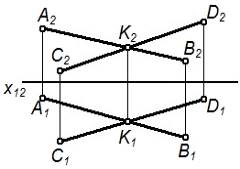  |
| Плоской фигурой | 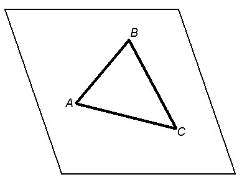  |
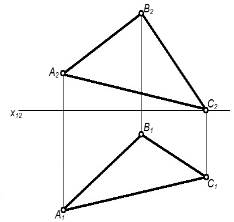  |
Возможны следующие положения плоскости относительно плоскостей проекции:
1) плоскость не перпендикулярна и не параллельна ни к одной плоскости проекций – общего положения (рисунок 15);
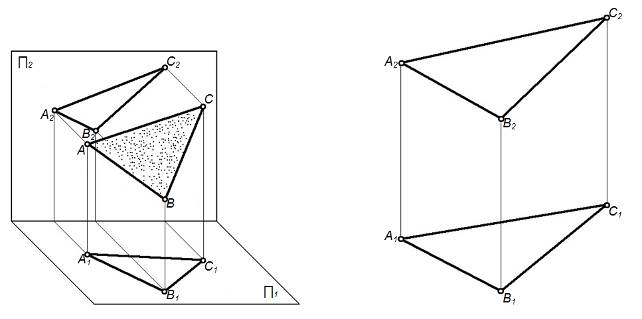
Рисунок 15 – Плоскость общего положения
2) плоскость перпендикулярна к какой-либо плоскости проекций – проецирующая (рисунок 16);
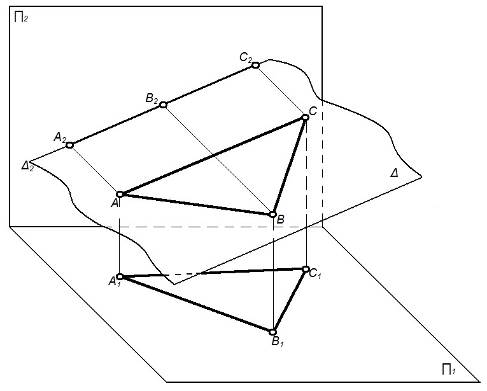
Рисунок 16 – Проецирующая плоскость
3) плоскость параллельна какой-либо плоскости проекций (дважды проецирующая) – плоскость уровня (рисунок 17).
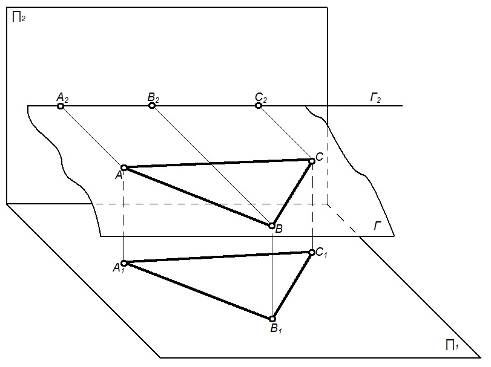
Рисунок 17 – Плоскость уровня
На комплексном чертеже рассматривается три проецирующих плоскости и три плоскости уровня (таблица 2).
Таблица 2 – Частные случаи расположения плоскостей
| ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ | |||
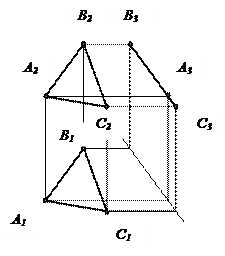
| Горизонтально-проецирующая плоскость | Фронтально-проецирующая плоскость | Профильно-проецирующая плоскость | |
| 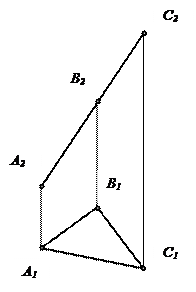  |
  |
|
| ПЛОСКОСТИ УРОВНЯ | |||
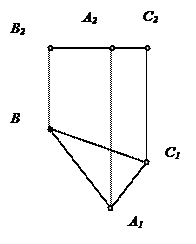
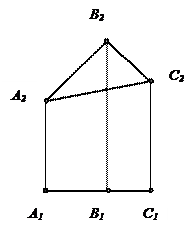
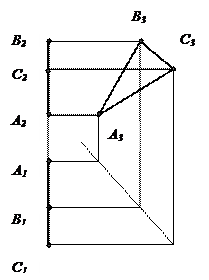
| Горизонтальная плоскость уровня | Фронтальная плоскость уровня | Профильная плоскость уровня | |
  |
  |
  |
Горизонтально проецирующая плоскость – ^П1. Горизонтальная проекция такой плоскости вырождается в прямую линию (главная проекция). Это главный признак горизонтально проецирующей плоскости на комплексном чертеже. Главная проекция плоскости обладает собирательными свойствами, т.е. проекции всех точек принадлежащих горизонтально проецирующей плоскости на П1 совпадают с главной проекцией этой плоскости.
Фронтально проецирующая плоскость – ^П2. Фронтальная проекция такой плоскости вырождается в прямую линию (главная прямая). Это признак фронтально проецирующей на комплексном чертеже. Главная проекция (проекция на П2) обладает собирательным свойством, т.е. проекции всех точек, принадлежащих фронтально проецирующей плоскости на П2 совпадают с главной проекцией этой плоскости.
Профильно проецирующая плоскость – ^П3. Профильная проекция такой плоскости вырождается в прямую линию (главная проекция). Это признак профильно проецирующей плоскости на комплексном чертеже. Главная проекция обладает собирательным свойством.
Горизонтальная плоскость уровня параллельна П1, одновременно такая плоскость является профильно и фронтально проецирующей.
Фронтальная плоскость уровня параллельна П2, одновременно горизонтально и профильно проецирующая плоскость.
Профильная плоскость уровня параллельна П3, одновременно горизонтально и фронтально проецирующая плоскость.
Задание 4. Найти проекцию точки Р(-8,12) на прямую, проходящую через точки А(2,- 3) и В(- 5.1)
Найти проекцию точки Р(-8,12) на прямую, проходящую через точки А(2,- 3) и В(- 5.1). Система координат прямоугольная.
Решение
Составим уравнение прямой, проходящую через точки


Прямая, перпендикулярная данной записывается в виде










То есть, проекция точки Р на прямую АВ есть точка

Задание 5
Определить положение точки М(-3, 2) относительно треугольника, стороны которого заданы уравнениями

Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: “Что-то тут концом пахнет”. 8266 –



185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Точка на прямой
Если точка лежит на прямой, то проекции этой точки лежат на одноименных проекциях прямой. Точка С лежит на прямой АВ, а точка D – не лежит на этой прямой (рис.21).

Деление отрезка в заданном отношении
Деление отрезка на равные или пропорциональные части выполняют по теореме Фалеса: Если на одной прямой отложить равные или пропорциональные отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на другой прямой равные или пропорциональные отрезки. Разделим отрезок АВ в соотношении 3:1 (рис.22).

Определение истинной величины отрезка прямой методом прямоугольного треугольника
В пространстве отрезок АВ прямой общего положения спроецирован на две плоскости π1 и π2 и представляет собой гипотенузу двух прямоугольных ∆ АВС и ABD (рис.23). В ∆ АВС катет АС параллелен и равен А’В’, катет СВ составляет разность координат z точек А и В. Катетами второго – отрезок BD=A”B” и разность координат у точек А и В. На эпюре легко построить такие треугольники.

Длина отрезка АВ определяется гипотенузой прямоугольного треугольника, одним из катетов которого является одна из проекций отрезка АВ, а вторым – разность координат концов отрезка. Угол между гипотенузой и горизонтальной проекцией является углом наклона отрезка АВ к плоскости π1 – α. β – угол наклона отрезка АВ к плоскости π2 является углом между гипотенузой и фронтальной проекцией отрезка АВ.
Чтобы на эпюре получить истинную величину отрезка АВ и углы его наклона α и β к плоскостям π1 и π2, нужно построить два прямоугольных треугольника (рис.24). Катетами одного треугольника является горизонтальная проекция А’В’ и разность ∆ z точек А и В. Гипотенузы АВ’ и АВ” равны длине отрезка АВ, а углы, заключенные между ними и проекциями А’B’ и А”В”, равны искомым углам α и β.

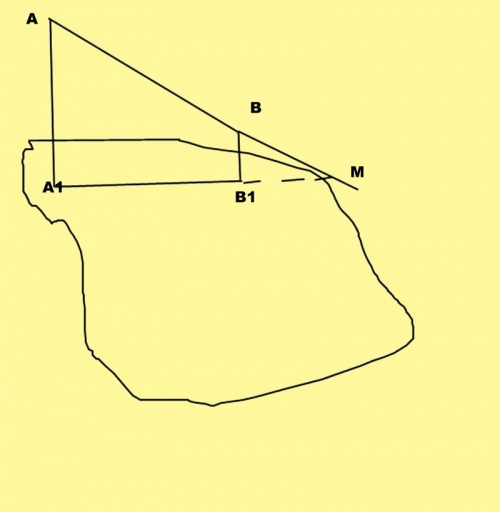
Проекция прямого угла
Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис.25).

Задача 1. Определить расстояние от точки А до прямой l (рис.26).
Решение сводится к построению перпендикуляра А’В’ на l’ и определению его истинной величины методом прямоугольного треугольника.
Задача 2. Построить равнобедренный треугольник с вершиной в точке А и одним из катетов на прямой l’ (рис.27).



Прямая l является фронталью. Строим прямой угол. Из А” на l” опускаем ┴АВ. Строим в проекционной связи горизонтальную проекцию отрезка А’B’.
Катет АВ (А’В’, А”В”) – отрезок общего положения. Истинную величину АВ находим методом прямоугольного треугольника и откладываем ее на фронтальной проекции фронтальной прямой l для получения вершины С.
Задача 3. Построить ромб ABCD по заданным вершине А и направлению диагонали BD на h и отношению диагоналей AC:BD=1:1,5 (рис.28).
Решение задачи сводится к построению диагоналей АС и BD.
О – точка пересечения диагоналей.

Находим истинную величину отрезка ОА методом прямоугольного треугольника и, увеличив ее в 1,5 раза, откладываем на h’ для получения проекций В’ и D‘. В” и D” находим на h”. Полученные проекции точек соединяем для получения проекций ромба.
геометрия – Как найти проекцию точки $%A(2;3;4)$% на прямую $%x = y = z$%?
Нашел вектор нормали $%(1,1,1)$%, а дальше не знаю, как делать.
задан 7 Окт ’12 20:23
Уравнение прямой можно записать в виде $%frac
отвечен 7 Окт ’12 21:21
Прямая $%x=y=z$% задается вектором направления $%overline v=overline$%. Преобразуем его к единичному вектору, разделим на его длину: $$|overline v|=sqrt=sqrt3$$ $$overline v_0=frac
отвечен 7 Окт ’12 20:39
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Проецирование прямого угла на плоскость проекций
Теорема о частном проецировании прямого угла
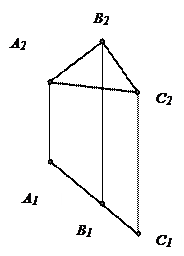
Если плоскость прямого угла не перпендикулярна и не параллельна плоскости проекций и хотя бы одна сторона его параллельна этой плоскости, то прямой угол проецируется на нее без искажения.
Пусть угол АВС – прямой (рис. 65) и сторона ВС || Н, следовательно, проекция bc || BC. Сторону АВ продолжим до пересечения с плоскостью Н и через точку К проводим прямую KN || bc. Следовательно, KN || BC.
Отсюда следует, что угол BKN – прямой. Согласно теореме о трех перпендикулярах, угол bKN – прямой, следовательно, угол Kbc = 90°.
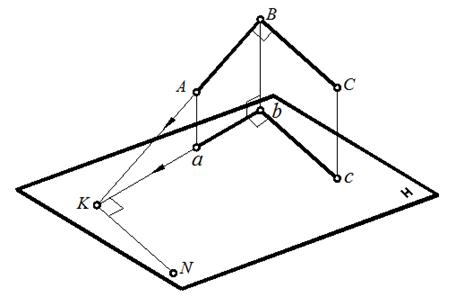
Рис. 65. Пространственная модель проецирования прямого угла
Примечание. Этой теореме о проецировании прямого угла соответствуют две обратные теоремы (доказательства не приводятся).
1. Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь при условии, что по крайней мере одна из сторон этого угла параллельна плоскости проекций.
2. Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет прямой угол, то проецируемый угол также прямой.
На основании этих теорем можно установить, что углы, изображенные на рис. 66, в пространстве – прямые.
|
|
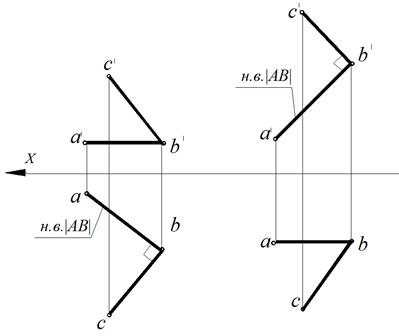
Рис. 66. Проецирование прямого угла на эпюре Монжа:
а – одна из сторон угла – горизонталь; б – одна из сторон угла – фронталь
Рассмотрим угол В (рис. 66а).
В пространстве угол В прямой, т. к. на эпюре видно, что прямая АВ является горизонталью (h′ || X) и ∠a = 90° (согласно первой обратной теореме).
Рассмотрим угол В (рис. 66б).
В пространстве угол В прямой, т. к. одна его сторона является фронталью (АВ || V; ab || X) и фронтальная проекция ∠b′ = 90°.
Из этой теоремы следует простой вывод – к прямой можно провести перпендикуляр там, где прямая проецируется в натуральную величину.
При решении позиционных и метрических задач начертательной геометрии, опираясь на эти теоремы, можно строить две взаимно перпендикулярные прямые, что, в конечном итоге, позволяет определять расстояния, строить взаимно перпендикулярные плоскости.
Рассмотрим несколько задач по теме данного материала.
Задача 1. Через точку А провести прямую, перпендикулярную прямой М (рис. 67).
Анализируя графическое условие задачи, отмечаем, что m || X, а это значит, что прямая М является фронталью (М || V).
Следовательно, построение искомой прямой надо начинать с фронтальной проекции, проводя ее перпендикулярно проекции m׳, т. к. на фронтальной плоскости проекций прямая М проецируется без искажения и на фронтальную плоскость проекций V прямой угол между данной и вновь построенной прямыми будет проецироваться без искажения.
Порядок выполнения графической части задачи:
1. Строим фронтальную проекцию искомого отрезка a′b′ ⊥ m′.
2. Определяем положение точки b׳ на проекции m׳ и по проекционной связи определяем горизонтальную проекцию b на проекции m.
3. Строим горизонтальную проекцию искомого отрезка ab.
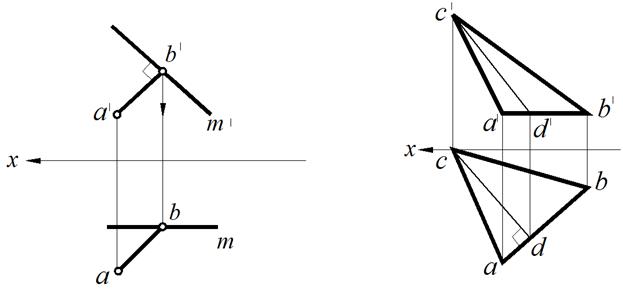
Рис. 67. Построение перпендикуляра к прямой М Рис. 68. Построение высоты в ∆АВС
Задача 2. Через вершину С провести высоту треугольника АВС (рис. 68).
Решение. Анализируем эпюр и отмечаем, что сторона треугольника АВ || H, при этом ее горизонтальная проекция отображается в натуральную величину.
Следовательно, построение высоты надо начинать с горизонтальной проекции.
Порядок выполнения графической части задачи:
1. Из точки с проводим отрезок перпендикулярно стороне ab.
2. Точка d –основание высоты, cd – горизонтальная проекция высоты.
3. Проецируем точку d на фронтальную проекцию стороны a′b′ и получаем фронтальную проекцию точки d′ и строим фронтальную проекцию высоты c′d′.
Задача 3. Определить расстояние от точки К до прямой N (рис. 69).
Решение. Следует отметить, что при решении задач на определение расстояний, необходимо строить не только проекции расстояния, но определять его натуральную величину.
Кратчайшим расстоянием от точки до прямой является величина перпендикуляра, опущенного из этой точки на прямую. Анализируя эпюр, отмечаем, что прямая N является фронталью и отображается на фронтальной проекции без искажения.
Следовательно, построение проекции перпендикуляра необходимо начинать с его фронтальной проекции.
Порядок выполнения графической части задачи:
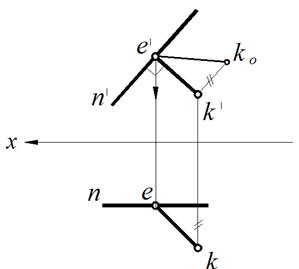
1. Из точки k′ опускаем перпендикуляр на проекцию прямой n′, получаем точку e′. Фронтальная проекция перпендикуляра – k′e′.
2. Проецируем полученную точку на горизонтальную проекцию прямой n, получаем точку e и горизонтальную проекцию перпендикуляра ke.
3. Судя по проекциям, прямая КЕ общего положения. Методом прямоугольного треугольника определяем ее натуральную величину |KE|.
Расстояние от точки К до прямой N равно длине отрезка – Кое′.
Прямые, занимающим особое положение в плоскости:
1. Линии уровня плоскости.
2. Линии наибольшего наклона плоскости к плоскостям проекций.
Линии уровня плоскости
Линии уровня плоскости– прямые, лежащие в заданной плоскости и параллельные плоскостям проекций: горизонтали, фронтали, профильные прямые.

Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости, горизонтальный след плоскости является нулевой горизонталью плоскости. Чтобы построить горизонталь в плоскости Р,заданной следами, надо на фронтальной проекции РVотметить точку d’ – фронтальную проекцию следа горизонтали (рис. 67а). Через нее проводим фронтальную проекцию горизонтали параллельно оси х. На оси х находим горизонтальную проекцию d. Прямая, проведенная из точки d параллельно следу РНплоскости, представляет горизонтальную проекцию горизонтали.
На рис. 70б проекции горизонтали проведены через проекции точки D и точки 1 прямой ЕС плоскости, заданной треугольником СDE. Построение горизонтали всегда начинают с фронтальной проекции d’1′, которая параллельна оси Х. По свойству принадлежности находят горизонтальную проекцию точки 1 и проводят горизонтальную проекцию горизонтали.
|
|
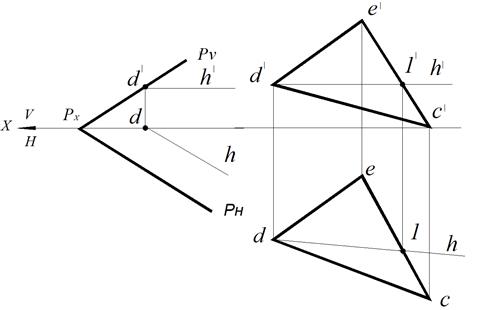
Рис. 70. Горизонталь плоскости:
а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆СDE
Фронталь плоскости – прямая, лежащая в плоскости и параллельная плоскости проекций V(рис. 71).
Построение фронтали и профильных прямых выполняется аналогично построению горизонтали, опираясь на известные свойства проекций линий уровня и свойство принадлежности, и начинают его с той проекции, которая параллельна соответствующей проекционной оси.Все фронтали одной и той же плоскости параллельны между собой. То же самое можно сказать и о профильных прямых уровня плоскости.
Профильная прямая уровня плоскости – это прямая, лежащая в данной плоскости и параллельная профильной плоскости проекций (рис. 72).
|
|
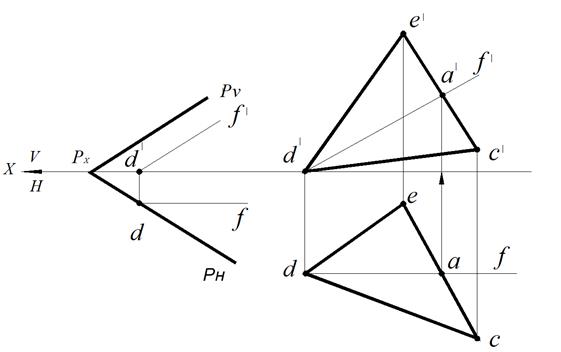
Рис. 71. Фронталь плоскости:
а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆СDE
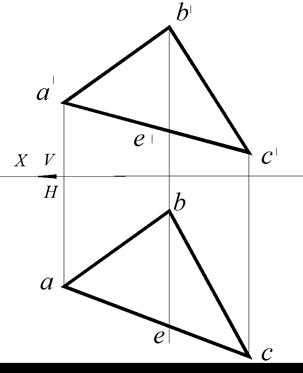
Рис. 72. Профильная прямая уровня ВЕ плоскости ∆АВС
Последнее изменение этой страницы: 2016-12-14; Нарушение авторского права страницы


Позвольте представиться. Меня зовут Татьяна. Я уже более 8 лет занимаюсь психологией. Считая себя профессионалом, хочу научить всех посетителей сайта решать разнообразные задачи. Все данные для сайта собраны и тщательно переработаны для того чтобы донести как можно доступнее всю необходимую информацию. Перед применением описанного на сайте всегда необходима ОБЯЗАТЕЛЬНАЯ консультация с профессионалами.