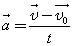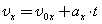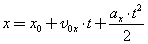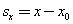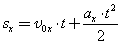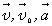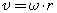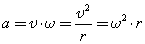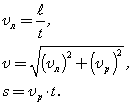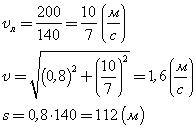Татьяна Ефимова предлагает статью на тему: "проекция скорости формула" с детальным описанием.
Содержание
1. МЕХАНИКА
1.1. Кинематика
Движение с ускорением
Равноускоренное прямолинейное движение – движение по прямой с постоянным ускорением (а = const ).
Ускорение а (размерность: м/с 2 ) – векторная физическая величина, показывающая, на сколько изменяется скорость тела за 1 с.
В векторном виде:
В проекции на ось ОХ формула аналогичная
Знаки проекции ускорения зависят от направления вектора ускорения и оси – сонаправлены они или направлены противоположно.
Измерительный прибор – акселерометр. (В ЕГЭ по физике есть вопросы, каким прибором что измеряют.)
График ускорения – зависимость проекции ускорения от времени:
График ускорения при равноускоренном прямолинейном движении – прямая, параллельная оси времени (1, 2).
Чем дальше график от оси времени (2), тем больше модуль ускорения.
Мгновенная скорость – скорость в данный момент времени или в данном месте пространства .
Скорость при равноускоренном прямолинейном движении.
В векторном виде,
в проекции на ось OX,
с учетом знака ускорения («+» разгон, «-» торможение):

График мгновенной скорости – зависимость проекции скорости от времени.
График скорости при равноускоренном прямолинейном движении – прямая (1, 2, 3). Если график располагается над осью времени, то тело движется по направлению оси ОХ.
Чем больше угол наклона графика (3), тем больше модуль ускорения.
Если график пересекает ось времени (2), то на первом этапе тело тормозило, в какой-то момент скорость его стала равной нулю, и далее тело двигалось ускоренно в противоположную сторону.
Геометрический смысл перемещения
| Так как | 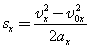 |
, то для координаты тела х имеем: | 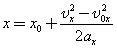 |
При вычислениях по приведенным формулам знаки проекций векторов
3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω.
Связь между линейной и угловой скоростью выражается формулой:
где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:
Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.
Пример решения задачи:
1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
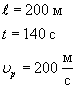  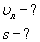 |
 |
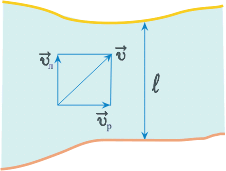 |
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.
Решите задачи самостоятельно:
1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?
2. 9 км/ч = . м/с; 10 м/с = . км/ч; 8 км/с = . км/ч, 54 км/ч = . м/с.
3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.
1. МЕХАНИКА
1.1. Кинематика
Механическое движение и его характеристики
Механика изучает самый простой и наглядный вид движения – механическое движение. Механическое движение – это изменение положения тела в пространстве, относительно других тел с течением времени.
По характеру движения точек различают три вида движения:
а) поступательное – это движение, при котором все точки
тела движутся одинаково и любая прямая, мысленно прове денная в теле, остается параллельна сама себе;
б) вращательное движение, при котором все точки тела движутся по окружностям;
в) колебательное движение – движение, которое повторяется или почти повторяется. В отличие от вращательного движения, колебательное происходит в двух взаимно противоположных направлениях.
По виду траектории различают прямолинейное и криволинейное движения (частный случай криволинейного движения – движение по окружности); по скорости – равномерное и неравномерное; по ускорению – равноускоренное, равнозамедленное, ускоренное.
Основная задача механики – определять положение тела в пространстве (координаты) в любой момент времени.
Материальная точка – это тело, размерами которого можно пренебречь в условиях данной задачи. Тело можно принять за материальную точку, если оно движется поступательно или если его размеры намного меньше расстояния, которые тело проходит.
Систему отсчета вводят для того, чтобы задать положение материальной точки в пространстве. В нее входят: тело отсчета (любое тело), система координат (одномерная, двумерная или трехмерная) и часы.
Траектория – линия, вдоль которой движется тело.
Путь – длина траектории.
Перемещение – это вектор, соединяющий начальное положение тела с конечным. Путь равен перемещению, если тело движется по прямой.
Хорошая новость: в задачах ЕГЭ нет подвохов на различие понятий путь и перемещение. Вам надо просто уметь считать путь для прямолинейного движения по соответствующим формулам.
- Тело, брошенное под углом к горизонту, движется по параболе. Длину участка параболы от вас найти не потребуют, это за рамками школьного курса.
- Если тело движется по окружности, то путь будет равен длине окружности, умноженной на число оборотов. Перемещение равно нулю при целом числе оборотов. Пока таких задач не замечено, но может появиться в категории С. Руководствуйтесь здравым смыслом, сделайте рисунок, чертеж.
Проекции вектора перемещения на оси координат
Знаки проекций перемещения: проекцию считают положительной, если движение от проекции начала вектора к проекции конца происходит по направлению оси, и отрицательной, если против оси. В примере на рисунке sx > 0; sy Забегая вперед.
- Если в задаче спрашивается: найдите изменение проекции или изменение величины проекции (например, проекции импульса), то действуйте по приведенным выше правилам.
- Чаще вам встретятся задачи, где надо нарисовать проекции сил на оси координат, (например, тело на наклонной плоскости). Одну ось выбирайте по направлению движения, вторую перпендикулярно. Проекции сил можно нарисовать в черновике со стрелочками для наглядности, чтобы понять, где плюс, где минус. Но дальше надо складывать их алгебраически, как числа.
Не запутайтесь: не пытайтесь складывать вектор силы с вектором проекции силы. Если выбрали две оси и нарисовали проекции, дальше надо писать уравнение для каждой из осей. Проекции сил, направленные против направления оси, будут с отрицательным знаком.
Уравнение координаты (в общем виде).
Радиус-вектор – вектор, начало которого совпадает с началом координат, а конец – с положением тела в данный момент времени. Проекции радиус-вектора на оси координат определяют координаты тела в данный момент времени. Радиус-вектор позволяет задать положение материальной точки в заданной системе отсчета.
пропускаем, потому что в задачах она не встречается.
Равномерное прямолинейное движение
Равномерное прямолинейное движение – движение, при котором тело за равные промежутки времени совершает равные перемещения. Обычно промежуток времени секунда, или час.
Скорость при равномерном прямолинейном движении
Скорость (м/с) – векторная физическая величина, которая показывает, какое перемещение совершает тело за единицу времени.
Встречается единицы измерения скорости:
1 км/ч = 1000 м / 3600 с
Измерительный прибор спидометр показывает модуль скорости.
График скорости при равномерном прямолинейном движении – прямая, параллельная оси времени (1, 2, 3). На индекс х не обращайте особого внимания. Имеется в виду, что выбрана некая ось координат.
Если график лежит над осью времени (1), то тело движется по направлению оси ОХ. Если график расположен под осью времени, то тело движется против оси Ох (2, 3).
Чем дальше график от оси времени, тем больше модуль скорости (случай 3).
Геометрический смысл перемещения
При равномерном прямолинейном движении перемещение определяют по формуле s = v • t . Такой же результат получим, если вычислим площадь фигуры под графиком скорости в осях ( v , t ). Значит, для определения пути и модуля перемещения при прямолинейном движении необходимо вычислить площадь фигуры под графиком скорости.
График проекции перемещения перемещения от времени.
График проекции перемещения при равномерном прямолинейном движении – прямая, выходящая из начала координат (1, 2, 3).
Если прямая (1) лежит над осью времени, то тело движется по направлению оси ОХ, а если под осью (2, 3), то против оси ОХ.
Чем больше тангенс угла наклона графика, тем больше модуль скорости (1).
График координаты – зависимость координаты тела от времени:
|
Все неприличные комментарии будут удаляться. Чему равна проекция скорости тела? (1 июля 2011)Источник: ЕГЭ 2011, О. Ф. Кабардин, С. И. Кабардина, В. А. Орлов. Помогите решить задачу, не сходится ответ, в ответах 0, у меня получается 3, хотя бы по порядку, что и как находим, а решу сам.
КомментарииОдин из вариантов: v = Δx/Δt = x / = (1 + 4t − 2t 2 ) / = 4 − 4t. В уравнение скорости: подставляем t = 1 c. Второй вариант предложите сами.
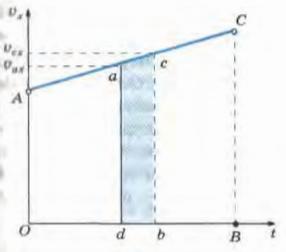
1) Можно через координаты, построив график зависимости x от t. У нас есть уравнение координаты, значит, xo = 1 м, так как t = 1 c, то подставим в уравнение координаты и получим: x = 1 + 4 × 1 − 2 × 1 × 1 = 3 м, то есть пройденный путь Δx = x − xo, или Δx = 3 − 1 = 2 м. 2) Можно найти путь, пройденный телом, по формуле Δx = vot − (at 2 )/2, или Δx = 4 × 1 − (4 × 1 × 1)/2 = 2 м. Теперь найдём скорость. 1) Можно по формуле Δx = (v 2 − vo 2 ) / (−2a) (минус, так как торможение, что видно из уравнения) или v = √(vo 2 − 2aΔx), то есть v = (4 × 4 − 2 × 4 × 2) = 0 м/c. 2) Можно по формуле Δx = (v + vo)/2, или v = (2Δx − vot)/t, то есть v = (2 × 2 − 4 × 1)/1 = 0 м/с. Проекция скорости формулаРавномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0). Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия. Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени. Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела               Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени. Перемещение при равномерном прямолинейном движении определяется формулой:               Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: Проекция перемещения на ось ОХ равна: где x – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени) Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид: Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v Равномерное прямолинейное движение – это частный случай неравномерного движения. Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений. Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково. Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const). Равнопеременное движение может быть равноускоренным или равнозамедленным. Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения. Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается. В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат. Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с. Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt: 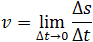 Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:               Проекция вектора скорости на ось ОХ: это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси). Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt: 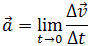 Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени: 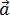 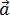                                  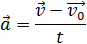 Отсюда формула скорости равнопеременного движения в любой момент времени:                  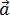 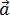 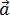 Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат. Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15). 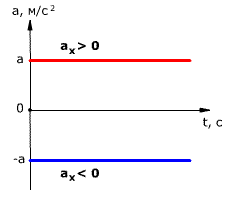 Рис. 1.15. Зависимость ускорения тела от времени. Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16). 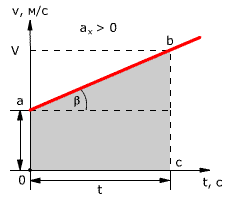 Рис. 1.16. Зависимость скорости тела от времени. График зависимости скорости от времени (рис. 1.16) показывает, что 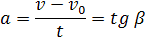 При этом перемещение численно равно площади фигуры 0abc (рис. 1.16). Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны: Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна: 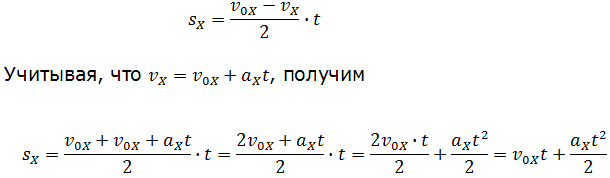 В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус). Общая формула для определения проекции перемещения: 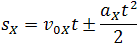 График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18. 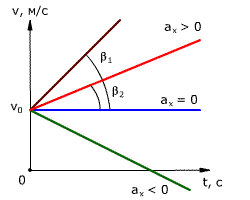 Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения. 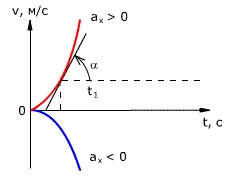 Рис. 1.18. Зависимость перемещения тела от времени. Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле: 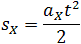 Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений: 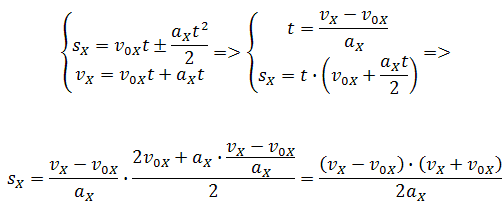 Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения: 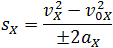 Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом: 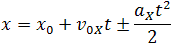 Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx Скорость прямолинейного равноускоренного движенияПроекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле: Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t. То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело в данной точке.
Графиком уравнения Vx=V0x+ax*t будет прямая линия. Расположение этой лини в системе координат будет определяться значениями ax b V0x. График проекции скорости тела при нулевой начальной скоростиНа следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел нулевую скорость, и двигалось равноускоренно и прямолинейно с ускорением ax=1,5 м/(с^2) в течение 40 секунд. 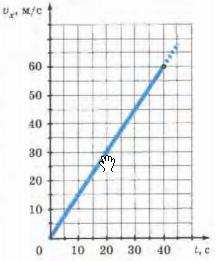 Так как изначально скорость была нулю, то уравнение примет следующий вид Для построения графика достаточно взять пару точек. Выберем момент времени t=40, тогда Vx= ax*t =1,5*40 = 60 Отметим эти точки на графике и соединим их прямой. Так как ускорение положительное, то график образует с осью Ох острый угол. График проекции скорости тела при ненулевой начальной скоростиТеперь посмотрим, как будет выглядеть график вектора проекции скорости, при начальной скорости тела отличной от нуля. В этом случае график будет описываться функцией Vx=V0x+ax*t. На следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел скорость Vx=10, и двигалось равноускоренно и прямолинейно с ускорением ax=1,4 м/(с^2) в течение 4 секунд.  Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость. График проекции скорости тела при торможенииЕсли бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол. Ниже представлен график такой ситуации. 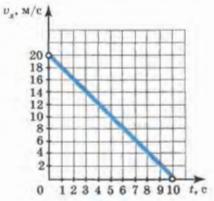 Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось. Нужна помощь в учебе?Предыдущая тема: Прямолинейное равноускоренное движение и ускорение
|














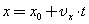
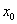
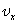 — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.
— проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.