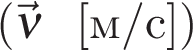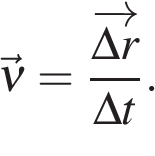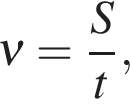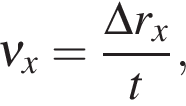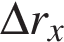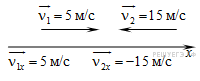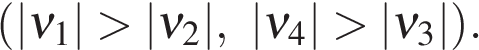1. МЕХАНИКА
1.1. Кинематика

Движение с ускорением

Равноускоренное прямолинейное движение – движение по прямой с постоянным ускорением (а = const ).

Ускорение а (размерность: м/с 2 ) – векторная физическая величина, показывающая, на сколько изменяется скорость тела за 1 с.

В векторном виде:

В проекции на ось ОХ формула аналогичная

Знаки проекции ускорения зависят от направления вектора ускорения и оси – сонаправлены они или направлены противоположно.

Измерительный прибор – акселерометр. (В ЕГЭ по физике есть вопросы, каким прибором что измеряют.)

График ускорения – зависимость проекции ускорения от времени:

График ускорения при равноускоренном прямолинейном движении – прямая, параллельная оси времени (1, 2).
Чем дальше график от оси времени (2), тем больше модуль ускорения.

Мгновенная скорость – скорость в данный момент времени или в данном месте пространства .

Скорость при равноускоренном прямолинейном движении.

В векторном виде,
в проекции на ось OX,
с учетом знака ускорения («+» разгон, «-» торможение):

График мгновенной скорости – зависимость проекции скорости от времени.

График скорости при равноускоренном прямолинейном движении – прямая (1, 2, 3). Если график располагается над осью времени, то тело движется по направлению оси ОХ.

Чем больше угол наклона графика (3), тем больше модуль ускорения.

Если график пересекает ось времени (2), то на первом этапе тело тормозило, в какой-то момент скорость его стала равной нулю, и далее тело двигалось ускоренно в противоположную сторону.

Геометрический смысл перемещения

Модуль перемещения при равноускоренном прямолинейном движенииравен площади трапеции под графиком скорости.

Формулы для определения кинематических величин равноускоренного прямолинейного движения:

“Без ускорения” и “без времени” означает, что в этих формулах не фигурирует ускорение и время, но это не значит, что ускорение равно нулю.
Цветом выделены основные формулы, остальные легко выводятся из них.

Уравнение координаты при равноускоренном прямолинейном движении позволяет определить кинематические величины равноускоренного прямолинейного движения даже в тех случаях, когда направление движения меняется:

Графики кинематических величин прямолинейного движения.
Их ндо уметь читать и рисовать. По горизонтальной оси обычно время. По вертикальной оси. будьте внимательны!

Свободное падение

Это частный случай движения с ускорением.

• Свободное падение происходит под действием только силы тяжести. Подробнее о связи силы с ускорением будет в теме “Динамика”, второй закон Ньютона.

• Сопротивление воздуха обычно не учитывается.

• Все тела независимо от массы падают (в вакууме или без учета сопротивления воздуха) с одинаковым ускорением.

• Ускорение свободного падения всегда направлено вниз, к центру Земли и равно g = 9,8 м/с 2 ; в задачах округляется до
g = 10 м/с 2 .

• Свободное падение по вертикали – пример равноускоренного прямолинейного движения.

• В задачах на свободное падение единицы измерения всех величин сразу следует переводить в СИ.

Основные формулы для определения кинематических величин при свободном падении (вертикальный бросок) те же, что даны выше. При этом ускорение a=g=10 м/с 2 .

Уравнение координаты при свободном падении позволяет определить кинематические величины свободного падения даже в тех случаях, когда направление движения изменяется. Уравнение координаты позволяет определить высоту тела в любой момент времени.

В разделе “Динамика” рассмотрим более сложные случаи:
– Тело подбросили от земли и поймали на некоторой высоте.
– Тело подбросили от земли, на одной и той же высоте оно побывало дважды.
– Горизонтальный бросок (движение по параболе). Бросок под углом к горизонту.

Проекции скорости и ускорения

Читайте также:

1. A – коэффициент скорости обучения.
2. Tраз – Длина отрезка проекции кривой Об на ось t
3. Адаптация человека в организации. Типы компенсации. Проекции человека в организационном поведении.
4. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
5. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
6. Анализ рентгенограммы грудной клетки в прямой проекции
7. Аналог относительной скорости двух точек М и N
8. Безразмерные скорости
9. Введение Г. Лейбницем понятия «живой силы» (энергии) как произведения массы тела на квадрат его скорости.
10. Векторные выражения скорости и ускорения точки вращающегося тела
11. Влияние интенсивности и скорости движения
12. Влияние скорости охлаждения и химического состава чугуна на графитизацию.

Единица ускорения.

Так как а = (v — v_o): t , то модуль ускорения равен единице, если равен единице модуль изменения скорости (v — v_o)и равен единице промежуток времени t. Поэтому за единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1 с скорость тела изменяется на 1 м/с. Следовательно, в СИ ускорение выражается в метрах в секунду за секунду или в метрах на секунду в квадрате (м/с 2 ).

Мы уже говорили, что при вычислениях нужно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат.

При прямолинейном движении векторы v и v направлены вдоль одной прямой. Эта прямая в то же время есть траектория движения. Вдоль этой же прямой удобно направить и координатную ось (например, ось X).

В § 5 мы видели, что проекция суммы двух векторов на какую-нибудь ось равна сумме их проекций на ту же ось. Обозначим проекции векторов v, v_o и а через v_x v_oх ,и а_х. Тогда из уравнения (2) следует, что

Так как все три вектора v, v и а лежат на одной прямой (на оси X), то модули их проекций равны модулям самих векторов, а знаки проекций определяются тем, как направлены векторы по отношению к оси. Если знаки проекции векторов v и а совпадают, то модуль скорости v возрастает с

течением времени — тело разгоняется. Если же знаки проекций v и а противоположны, то модуль скорости v с течением времени уменьшается — тело тормозится. Векторы v, v и а при движении с возрастающей скоростью сонаправлены. При торможении вектор а направлен противоположно векторам v и v_0.

Дата добавления: 2014-01-14 ; Просмотров: 525 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Проекции скорости движения

Главная цель Проверялкина – тренировка умения работать с параграфом: находить/выделять нужные по смыслу фрагменты, выбирать из нескольких подходящих фрагментов более удачный, многократно обращаться к тексту для поиска очередного ответа. В результате ваша зрительная память «схватывает» расположение в тексте важных моментов: определений, закономерностей, выводов; вы привыкаете к терминам и формулировкам. Другими словами, неоднократно перечитывая текст при поиске наилучшего ответа, вы полнее и обдуманнее воспринимаете физику.

Как и любой человек, Проверялкин «хочет» видеть не любой правильный ответ, а тот, который он считает наилучшим. Не расстраивайтесь, просто поищите другой ответ. Ведь разве плохо то, что вы будете знать несколько правильных ответов на один вопрос. Мы рекомендуем обсуждать задания с одноклассниками через наушники с микрофоном (или по телефону).

Важно: для Проверялкина правильным ответом является не только содержательно правильный, но и правильно «добытый». То есть ответы на задания Проверялкина нужно «перетаскивать» из параграфа, а не печатать «от себя» или копировать из других источников, например «готовых домашних заданий». Давайте вспомним, какова главная цель вашей беседы с Проверялкиным? Правильно – тренировка умения работать с материалом параграфа учебника!

Для перехода к проверялкам по темам кликайте номера тем вверху: 01 02 03 04 05 и т.д.

Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей

Чему равна проекция скорости тела? (1 июля 2011)

Источник: ЕГЭ 2011, О. Ф. Кабардин, С. И. Кабардина, В. А. Орлов.

Помогите решить задачу, не сходится ответ, в ответах 0, у меня получается 3, хотя бы по порядку, что и как находим, а решу сам.

• версия для печати
• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Комментарии

Один из вариантов:

v = Δx/Δt = x / = (1 + 4t − 2t 2 ) / = 4 − 4t.

В уравнение скорости:

подставляем t = 1 c.

Второй вариант предложите сами.

• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

1) Можно через координаты, построив график зависимости x от t. У нас есть уравнение координаты, значит, x_o = 1 м, так как t = 1 c, то подставим в уравнение координаты и получим: x = 1 + 4 × 1 − 2 × 1 × 1 = 3 м, то есть пройденный путь Δx = x − x_o, или Δx = 3 − 1 = 2 м.

2) Можно найти путь, пройденный телом, по формуле Δx = v_ot − (at 2 )/2, или Δx = 4 × 1 − (4 × 1 × 1)/2 = 2 м.

Теперь найдём скорость.

1) Можно по формуле Δx = (v 2 − v_o 2 ) / (−2a) (минус, так как торможение, что видно из уравнения) или v = √(v_o 2 − 2aΔx), то есть v = (4 × 4 − 2 × 4 × 2) = 0 м/c.

2) Можно по формуле Δx = (v + v_o)/2, или v = (2Δx − v_ot)/t, то есть v = (2 × 2 − 4 × 1)/1 = 0 м/с.

Прямолинейное равномерное движение

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

Проекция перемещения на ось ОХ равна:

где x – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

где α – угол наклона графика к оси времени.Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Проекции скорости движения

Математика

В этом разделе представлены теория и задачи по математике, необходимые для успешной подготовки к ЦТ или ЕГЭ. Список основных тем из школьной математики:

Смотрите также:

В этом разделе представлены теория и задачи по физике, необходимые для успешной подготовки к ЦТ или ЕГЭ. Список основных тем из школьной физики:

Смотрите также:

Формулы, методы и другая справочная информация

В этом разделе сайта представлены различные списки формул по физике и математике, а также приведена другая необходимая справочная информация. Знание физических и математических формул и методов является одним из ключевых элементов успешной подготовки к ЦТ или ЕГЭ. В этом разделе смотрите:

Итоговые тесты по физике и математике

В этом разделе сайта представлены итоговые тесты по физике и математике, которые позволят абитуриентам успешно повторить изученный материал и систематизировать свои знания по физике и математике. Решение этих тестов поможет поступающим успешно сдать ЦТ или ЕГЭ.

Другая полезная информация для абитуриентов

В этом разделе сайта представлены различные советы и рекомендации по подготовке и сдаче ЦТ и ЕГЭ. А также советы о том, как правильно организовать процесс изучения физики и математики дома для абитуриентов. В этом разделе смотрите:

Высшая математика

В этом разделе сайта приведена теория, задачи, тесты и формулы по высшей математике. Эта информация поможет поступившим в ВУЗы ученикам разобраться в этом сложном предмете и получить отличные оценки на экзаменах в ВУЗе. Представлена информация в следующих категориях:

Материалы для поступающих в Польшу

В этом разделе собраны материалы, которые помогут ученикам подготовится и поступить в польский университет. В основном материалы представляют из себя польские тесты по многим предметам, в том числе по физике и математике, но имеется также и другая полезная информация.

Научно-популярные статьи

В этом разделе собраны различные интересные факты в виде научно-популярных статей, в которых сложные вещи излагаются простым языком без лишних формул. Эти статьи помогут убедиться в особенной занимательности науки, полюбить физику и математику, а также отвлечься и развеяться во время трудоемкой и скучной подготовки к экзаменам.

ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их распространение, перепечатка или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону.

График проекции скорости от времени.

Скорость.

Равномерное прямолинейное движение.

2.1.1 Равномерное прямолинейное движение — это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, двигаясь по прямой линии.

2.1.2 Скорость

— векторная физическая величина, показывающая какое перемещение совершило тело за единицу времени:

При равномерном движении по прямой:

где S — путь, проходимый телом за время t.

Для учета направления движения эту формулу запишем в проекциях:

где

— перемещение вдоль оси Ox за время t. Знак проекции зависит от направления скорости и оси координат (см. рис.):

График проекции скорости от времени.

Так скорость при равномерном движении по прямой является постоянной, то график будет представлять собой прямые линии, параллельные оси времени (см. рис.):

Направление движения: если график лежит над осью времени (1 и 2), то проекция положительна и тело движется по направлению оси Ox; в противном случае, когда график расположен ниже оси времени (3 и 4), то проекция скорости отрицательна и тело движется против оси Ox.

Значение скорости: чем дальше от оси времени лежит прямая, тем больше модуль скорости

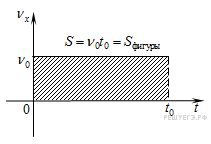
2.1.4 Геометрический смысл площади под графиком в осях .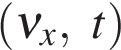

Для любого вида движения пройденный телом путь можно определить как площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время. Это легко видеть непосредственно из рисунка для равномерного движения (см. рис.):

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: “Что-то тут концом пахнет”. 8266 –

| 7903 – или читать все.

185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Равномерное прямолинейное движение. Скорость.

Равномерным и прямолинейным движением (РПД) называется такое движение по прямой при котором тело за любые одинаковые промежутки времени проходит одинаковые расстояния

Иногда определение равномерного прямолинейного движения понимают неправильно, типичной ошибкой является следующая: Пусть автомобиль за первый час прошел 60 километров и за второй час движения прошел тоже 60 километров. Будет ли его движение равномерным и прямолинейным.
Многие сразу отвечают, что такое движение будет являться РПД, так как тело за равные промежутки времени (1 час) прошло одинаковое расстояние. Но на самом деле для решения этой задачи нам не хватает данных, так как мы не имеем информацию о расстоянии проходимом за любой момент времени, так как чтобы движение было РПД необходимо, чтобы за любые одинаковые промежутки времени тело проходило одинаковые расстояния, а в данном случае мы не знаем проходит ли тело за первые полчаса расстояние равное расстоянию проходимому за вторые полчаса, равно ли расстояние за первую секунду расстоянию за вторую секунду и т.д.
Тогда можно сформулировать еще одно определение РПД:

Равномерным прямолинейным движением называется движение с постоянной мгновенной скоростью.

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела

за любой промежуток времени к значению этого промежутка t:

= / t

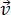
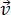
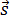
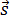
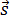
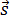
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

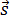
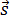
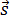
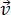
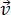
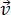
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

Проекция перемещения на ось ОХ равна:

где x – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения , то есть зависимость координаты тела от времени х = х(t), принимает вид:

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Зависимость скорости, координат и пути от времени

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

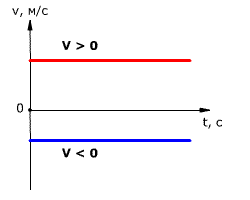
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

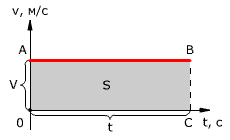
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

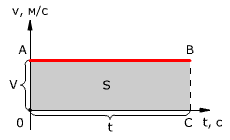
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

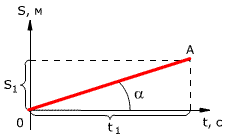
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

где α – угол наклона графика к оси времени.

Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

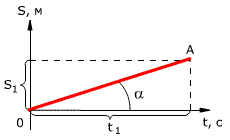
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

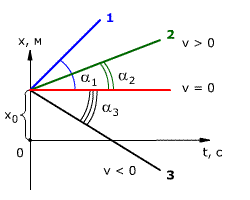
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Тесты: Равномерное прямолинейное движение

№22. По заданным графикам (рис. 9) найти начальные координаты тел и проекции скорости их движения. Написать уравнения движения тел х = x(t). Из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками II и III.

Решебник по физике за 10, 11 класс (А.П. Рымкевич, 2001 год),
задача №22
к главе «МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 2. Прямолинейное равномерное движение».

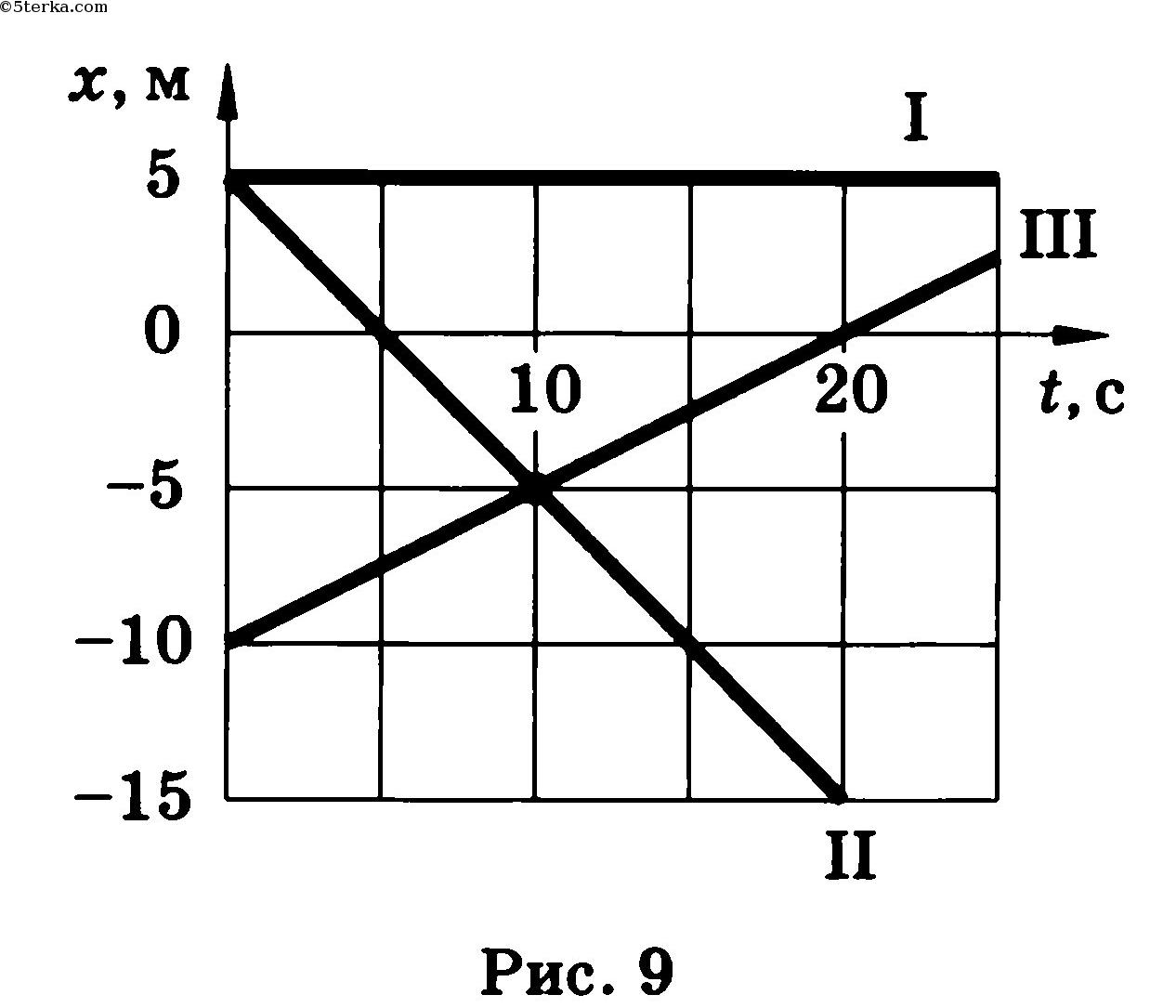
По графику видно, что начальные координаты I тела : 5 м, II: 5 м,

III: — 10 м. Скорости движения I:

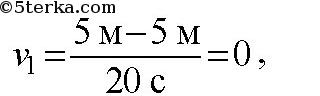
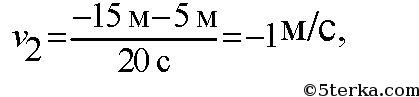
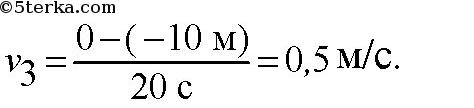
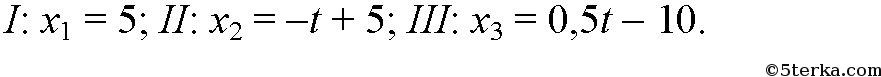
Т.к. движение равномерное вдоль оси Х, то найденные нами скорости v₁, v₂, v₃ являются проекциями на ось Х.

По графикам уравнения движения тел II и III видно, что они пересекутся в точке х = – 5 м в момент времени t = 10 с. Найдем это из уравнений движения.

физический словарик (кинематика)

Скорость (v) – физическая величина, численно равна пути (s), пройденного телом за единицу времени (t).

Путь (S) – длина траектории, по которой двигалось тело, численно равен произведению скорости (v) тела на время (t) движения.

Время движения

Время движения (t) равно отношению пути (S), пройденного телом, к скорости (v) движения.

Средняя скорость

Средняя скорость (vср) равна отношению суммы участков пути (s₁ s₂, s₃, . ), пройденного телом, к промежутку времени (t₁+ t₂+ t₃+ . ), за который этот путь пройден.

Средняя скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Средняя скорость при неравномерном движении по прямой:

это отношение всего пути ко всему времени.

Два последовательных этапа с разными скоростями:

где

При решении задач – сколько этапов движения столько будет составляющих:

Проекции вектора перемещения на оси координат

Проекция вектора перемещения на ось ОХ:

Проекция вектора перемещения на ось OY:

Проекция вектора на ось равна нулю, если вектор перпендикулярен оси.

Знаки проекций перемещения: проекцию считают положительной, если движение от проекции начала вектора к проекции конца происходит по направлению оси, и отрицательной, если против оси. В данном примере

Модуль перемещения – это длина вектора перемещения:

По теореме Пифагора:

Проекции перемещения и угол наклона

В данном примере:

Уравнение координаты (в общем виде):

Радиус-вектор — вектор, начало которого совпадает с началом координат, а конец — с положением тела в данный момент времени. Проекции радиус-вектора на оси координат определяют координаты тела в данный момент времени.

Радиус-вектор позволяет задать положение материальной точки в заданной системе отсчета:

Равномерное прямолинейное движение – определение

Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени, совершает равные перемещения.

Скорость при равномерном прямолинейном движении. Скорость

— векторная физическая величина, которая показывает, какое перемещение совершает тело за единицу времени.

В векторном виде:

В проекциях на ось ОХ:

Дополнительные единицы измерения скорости:

1 км/ч = 1000 м/3600 с,

Измерительный прибор — спидометр — показывает модуль скорости.

Знак проекции скорости зависит от направления вектора скорости и оси координат:

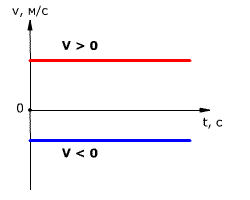
График проекции скорости представляет собой зависиость проекции скорости от времени:

График скорости при равномерном прямолинейном движении — прямая, параллельная оси времени (1, 2, 3).

Если график лежит над осью времени (.1), то тело движется по направлению оси ОХ. Если график расположен под осью времени, то тело движется против оси ОХ (2, 3).

Чем дальше график от оси времени, тем больше модуль скорости (3).

Геометрический смысл перемещения.

При равномерном прямолинейном движении перемещение определяют по формуле

. Такой же результат получим, если вычислим площадь фигуры под графиком скорости в осях . Значит, для определения пути и модуля перемещения при прямолинейном движении необходимо вычислять площадь фигуры под графиком скорости в осях :

График проекции перемещения — зависимость проекции перемещения от времени.

График проекции перемещения при равномерном прямолинейном движении — прямая, выходящая из начала координат (1, 2, 3).

Если прямая (1) лежит над осью времени, то тело движется по направлению оси ОХ, а если под осью (2, 3), то против оси ОХ.

Чем больше тангенс утла наклона (1) графика, тем больше модуль скорости.

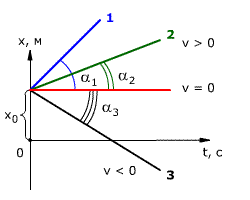
График координаты — зависимость координаты тела от времени:

График координаты при равномерном прямолинейном движении — прямые (1, 2, 3).

Если с течением времени координата увеличивается (1, 2), то тело движется по направлению оси ОХ; если координата уменьшается (3), то тело движется против направления оси ОХ.

Чем больше тангенс угла наклона (1), тем больше модуль скорости.

Если графики координат двух тел пересекаются, то из точки пересечения следует опустить перпендикуляры на ось времени и ось координат.

Относительность механического движения

Под относительностью мы понимаем зависимость чего-либо от выбора системы отсчета. Например, покой относителен; движение относительно и положение тела относительно.

Правило сложения перемещений. Векторная сумма перемещений

где

— перемещение тела относительно подвижной системы отсчета (ПСО); — перемещение ПСО относительно неподвижной системы отсчета (НСО); — перемещение тела относительно неподвижной системы отсчета (НСО).

Векторное сложение:

Сложение векторов, направленных вдоль одной прямой:

Сложение векторов, перпендикулярных друг другу

По теореме Пифагора

Сложение векторов, расположенных под углом друг к другу

Правило сложения скоростей. Векторная сумма скоростей:

где

— скорость тела относительно подвижной системы отсчета (ПСО); — скорость ПСО относительно неподвижной системы отсчета (НСО); — скорость тела относительно неподвижной системы отсчета (НСО).

Относительная скорость. Векторная разность скоростей:

где

— скорость первого тела относительно второго (относительная скорость); — скорость первого тела; — скорость второго тела.

Вычитание векторов, направленных по одной прямой:

Вычитание векторов перпендикулярных друг другу

Вычитание векторов, расположенных под углом друг к другу: