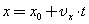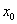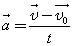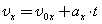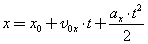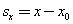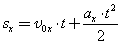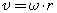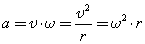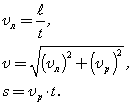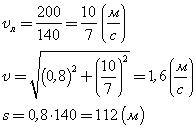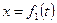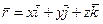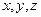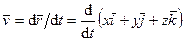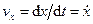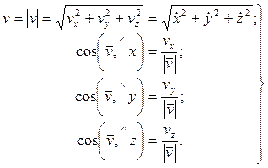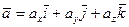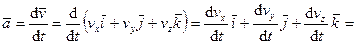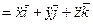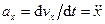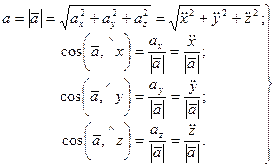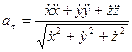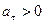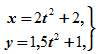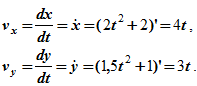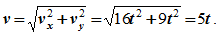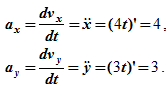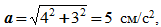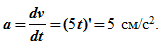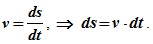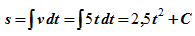Проекции скорости точки на оси координат

Теоретический материал, модули 1-4

Загрузить всю книгу

Титульный лист

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Тольяттинский государственный университет

Кафедра теоретической механики

ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ

для студентов, обучающихся по образовательной технологии «30/70»

Составил: к.ф.-м.н., доцент Прасолов С. Г.

к.т.н., доцент Будаев С. И.

Научный редактор: ст. преп. Шадрина С.П.

Утверждено научно-методическим советом университета.

© Тольяттинский государственный университет, 2005

Проекции скорости точки на оси координат

Материалы к зачету по теме “Основные законы механики “

1. Механическое движение.
Явление механического движения тел (материальных точек)состоит в том, что положение тела относительно других тел, т. е. его координаты, с течением времени изменяется.Чтобы найти координаты тела в любой момент времени, нужно знать начальные координаты и вектор перемещения тела. Изменение координаты тела равно проекции вектора перемещения на соответствующую ось координат.

Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:

,

где

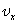— начальная координата тела, а — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.

Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.

Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется.

2. Основная задача механики
состоит в нахождении положения тела в любой момент времени. Решение этой задачи идет по своеобразной «цепочке»:
чтобы найти координату точки, нужно знать ее перемещение, а чтобы вычислить перемещение, нужно знать скорость движения.
По такой цепочке: скорость → перемещение → координата решают задачи механики для прямолинейного равномерного движения.

Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
При прямолинейном ускоренном движении мгновенная скорость тела (материальной точки) непрерывно изменяется от одного момента времени к другому. Поэтому для вычисления скорости в любой момент времени и в любой точке нужно знать быстроту ее изменения, т.е. ускорение:

.

Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле:

.

Координату тела находят по формуле:

.

Проекцию перемещения находят по формуле:

.

Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0.

Значение проекции перемещения при равноускоренном движении можно определить также по формуле:

.

Так как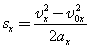

, то для координаты тела х имеем: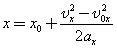

При вычислениях по приведенным формулам знаки проекций векторов

, а также знак начальной координаты х, определяются условием задачи и направлением оси координат.

3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса &#966, проведенного из центра окружности к телу, и угловой скорости ω.

Связь между линейной и угловой скоростью выражается формулой:

,

где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:

.

Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.

Пример решения задачи:

1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.

Вычисления:

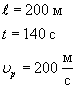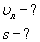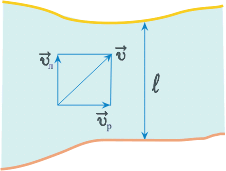Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.

Решите задачи самостоятельно:

1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?

2. 9 км/ч = . м/с; 10 м/с = . км/ч; 8 км/с = . км/ч, 54 км/ч = . м/с.

3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.

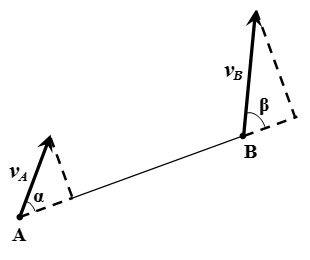
Теорема о проекциях скоростей двух точек твердого тела на прямую

Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.
v_A cos α = v_B cos β .

Доказательство

Выберем прямоугольную неподвижную систему координат Oxyz . Возьмем две произвольные точки твердого тела A и B . Пусть ( x_A, y_A, z_A ) и ( x_B, y_B, z_B ) – координаты этих точек. При движении твердого тела они являются функциями от времени t . Дифференцируя по времени, получаем проекции скоростей точек.
, .

Воспользуемся тем, что при движении твердого тела, расстояние | AB | между точками остается постоянным, то есть не зависит от времени t . Также постоянным является квадрат расстояния
.
Продифференцируем это уравнение по времени t , применяя правило дифференцирования сложной функции.

Сократим на 2 .
(1)

Введем вектор
.
Тогда уравнение (1) можно представить в виде скалярного произведения векторов.
(2)
Выполняем преобразования.
;
(3) .
По свойству скалярного произведения
,
.
Подставляем в (3) и сокращаем на | AB | .
;

Что и требовалось доказать.

Относительная скорость

Рассмотрим движение точки B относительно точки A . Введем относительную скорость точки B относительно A .

Тогда уравнение (2) можно переписать в виде
.

То есть относительная скорость перпендикулярна вектору , проведенному из точки A в точку B . Поскольку точка B взята произвольным образом, то относительная скорость любой точки твердого тела перпендикулярна радиус вектору, проведенному из точки A . То есть относительно точки A тело совершает вращательное движение. Относительная скорость точек тела определяется по формуле для вращательного движения
.

Точку A , относительно которой рассматривают движение, часто называют полюсом.

Абсолютную скорость точки B относительно неподвижной системы координат можно записать в следующем виде:
.
Она равна сумме скорости поступательного движения произвольной точки A (полюса) и скорости вращательного движения относительно полюса A .

Пример решения задачи

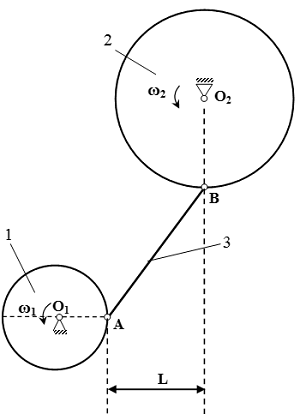
Колеса 1 и 2 с радиусами R ₁ = 0,15 м и R ₂ = 0,3 м , соответственно, соединены шарнирами со стержнем 3 длины | AB | = 0,5 м . Колесо 1 вращается с угловой скоростью ω ₁ = 1 рад/с . Для изображенного на рисунке положения механизма, определить угловую скорость ω ₂ колеса 2. Принять L = 0,3 м .

Точка A движется по окружности радиуса R ₁ вокруг центра вращения O ₁ . Скорость точки A определяется по формуле
V_A = ω ₁ R ₁ .
Вектор направлен вертикально (перпендикулярно O ₁ A ).

Точка B движется по окружности радиуса R ₂ вокруг центра вращения O ₂ . Скорость точки B определяется по формуле
V_B = ω ₂ R ₂ .
Отсюда
.
Вектор направлен горизонтально (перпендикулярно O ₂ B ).

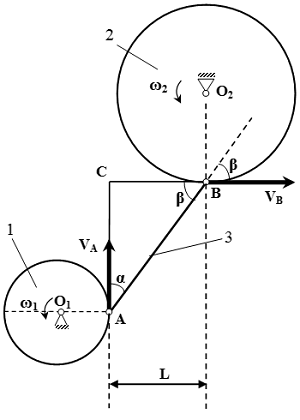
Строим прямоугольный треугольник ABC . Применяем теорему Пифагора.
(м)
Косинус угла между вектором скорости и прямой AB , в направлении вектора , равен
.
Косинус угла между вектором скорости и прямой AB , в направлении вектора , равен
.

По теореме о проекциях скоростей двух точек твердого тела на прямую имеем:
V_A cos α = V_B cos β .
Отсюда
.

Находим угловую скорость колеса 2.
рад/с .

Автор: Олег Одинцов . Опубликовано: 07-10-2015

Координатный способ задания движения точки

Движение точки в декартовых координатах считается заданным, если известны координаты точки как непрерывные, дважды дифференцируемые функции времени (рис. 24), т. е. заданы уравнения движения точки в декартовых координатах:

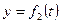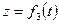, , . (50)

Уравнения движения точки в декартовых координатах полностью определяют движение точки. Они позволяют найти положение точки, ее скорость и ускорение в любой момент времени.

Разложим радиус-вектор и скорость точки на составляющие, параллельные осям координат. Получим

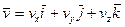, , (51)

где

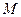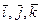– координаты точки ; – единичные векторы осей координат; 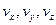– проекции скорости на оси координат.

Учитывая (51), согласно определению скорости, имеем:

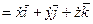, (52)

Сравнивая (52) и (51), получаем для проекций скорости на декартовы оси координат следующие формулы:

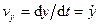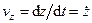, , . (53)

Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки. По проекциям определяют числовое значение (модуль) скорости и косинусы углов вектора скорости с осями координат:

(54)

Разложим ускорение точки на составляющие, параллельные осям декартовой системы координат. Получим

, (55)

где

– проекции ускорения на координатные оси. Согласно определению ускорения и формулам (52) и (51), имеем

. (56)

Формулы для проекций ускорения на оси декартовой системы координат:

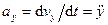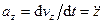, , . (57)

Проекция ускорения на какую-либо координатную ось равна второй производной по времени от соответствующей координаты движущейся точки.

Числовое значение ускорения и косинусы углов вектора ускорения с осями координат определяем по формулам

. (58)

Касательная и нормальная составляющие ускорения вычисляются по формулам:

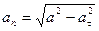, . (59)

При

движение точки ускоренное, при 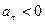– замедленное.

|	следующая лекция ==>
Скорость и ускорение точки	|	Естественный способ задания движения точки

Дата добавления: 2017-09-19 ; просмотров: 313 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Проекция вектора скорости на оси координат

В векторной форме уравнения записываются легко и кратко. Но для практических вычислений нужно знать проекции вектора на оси координат выбранной системы отсчета. Положение точки А (рис. 2.8) задается радиус-вектором г . Спроецируем вектор г на оси х,у, z.

Рис. 2.8. Вектор перемещения точки А и её скорость 1)

Понятно, что х, у₉ z зависят от времени t, т. е. *(/), y(t), z(t). Зная зависимость этих координат от времени (закон движения точки), можно найти в каждый момент времени скорость точки.

Проекции вектора скорости и на оси x,y₉z в обозначениях Лейбница:

Эти три равенства эквивалентны векторному равенству и = —.

Согласно общей формуле (2.2.2) модуль вектора скорости

Так как скорость – величина векторная, то её можно представить с помощью единичных векторов i, j, k :

Ускорение и его составляющие

В произвольном случае движения скорость нс остается постоянной. Быстрота изменения скорости по времени и направлению характеризуется ускорением

Ускорение – величина векторная. При криволинейном движении и изменяется также и по направлению. В какую сторону? С какой скоростью? Выражение (2.3.8) на эти вопросы не отвечает.

Введем единичный вектор т (рис. 2.9), связанный с точкой А и направленный по касательной к траектории движения точки А (векторы т и и в точке А совпадают). Тогда можно записать:

где о = |о| – модуль вектора скорости.

Рис. 2.9. К выводу тангенциальной составляющей ускорение: единичный вектор х направлен по касательной к траектории

Найдем ускорение:

Получаем два слагаемых ускорения: a_х – тангенциальное ускоре-

пие, совпадающее с направлением о в данной точке, а_п – нормальное ускорение, или центростремительное, т. к. направлено оно к центру кривизны, перпендикулярно вектору т .

где do/dt – скорость изменения модуля вектора скорости о.

Итак, a_z показывает изменение вектора скорости по величине:

• • если do/d/ > 0, то а_г направлено в ту же сторону, что и вектор о, т. е. ускоренное движение;
• • если do/d/ 0), центры кривизны О и О’ сливаются и угол поворота Д d dx d r dx i) 2 r

Tогда — = —, следовательно — = — n ; наконец, и — = — n , т. с.

Нормальное ускорение показывает быстроту изменения направления вектора скорости. Модуль нормального ускорения

Центростремительным называют ускорение, когда движение происходит по окружности. А когда движение происходит по произвольной кривой, говорят, нормальное ускорение, перпендикулярное к касательной в любой точке траектории.

Итак, возвращаясь к выражению (2.3.9), можно записать, что суммарный вектор ускорения при движении точки вдоль плоской кривой равен:

На рис. 2.11 изображено взаимное расположение векторов ускорения:

Рис. 2.11. Суммарное ускорение, нормальная и тангенциальная составляющие ускорения

Как видно из этого рисунка, модуль общего ускорения равен:

Рассмотрим несколько предельных (частных) случаев:

• • а_Т = 0; а_п = 0 – равномерное прямолинейное движение;
• • а_х = const ;а_п = 0 – равноускоренное прямолинейное движение;
• • а_х – 0; а_п = const – равномерное движение по окружности.

Прямая задача кинематики сводится к определению кинематических характеристик по известному закону движения.

При движении с постоянным ускорением (а = const)

Если и = о ± at (а = const), то

Обратная задача кинематики заключается в нахождении закона движения по известной скорости (ускорению) и начальному кинематическому состоянию.

Пусть нам известно ускорение точки в каждый момент времени.

Лекции и примеры решения задач по теормеху, сопромату, ТММ и ДМ

где x и y – в см, а t – в с. Определить траекторию движения точки, скорость и ускорение в моменты времени t=0 с, t₁=1 с и t₂=5 с, а также путь, пройденный точкой за 5 с.

Расчет траектории

Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе – на (-4), а затем складываем их левые и правые части:

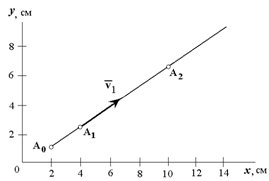
Получилось уравнение первой степени – уравнение прямой линии, значит движение точки – прямолинейное (рисунок 1.5).

Для того, чтобы определить координаты начального положения точки A, подставим в заданные уравнения значения t=0; из первого уравнения получим x=2 см, из второго y=1 см. При любом другом значении t координаты x и y движущейся точки только возрастают, поэтому траекторией точки служит полупрямая 3x-4y=2 с началом в точке A (2; 1).

Расчет скорости

Расчет ускорения

Определяем ускорение точки. Его проекции на оси координат:

Проекции ускорения не зависят от времени движения,

т.е. движение точки равноускоренное, векторы скорости и ускорения совпадают с траекторией точки и направлены вдоль нее.

С другой стороны, поскольку движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:

Определение пути

Определяем путь, пройденный точкой за первые 5с движения. Выразим путь как функцию времени:

Проинтегрируем последнее выражение:

Если t=t=0, то C=s; в данном случае s=0, поэтому s=2,5t 2 . Находим, что за 5с точка проходит расстояние

Скорость точки. Скорость и ускорение точки при координатном способе задания движения

Читайте также:

1. I. Понятие о контрразведке как о борьбе с военным шпионством в отличие от обывательской на нее точки зрения. Возможность успешности этой борьбы
2. IX. Порядок заполнения и представления статистической карточки формы N 6
3. VI. Порядок заполнения и представления статистической карточки формы N 3
4. VIII. Порядок заполнения и представления статистической карточки формы N 5
5. Акупунктурные точки на теле человека
6. Анализ текста с точки зрения профессиональной этики журналиста
7. Антропометрические точки
8. Болевые точки
9. Бонитет – показатель продуктивности леса, отражающий скорость роста деревьев.
10. В землю косточки сажает.
11. В тяге скорость не увеличивается, все вагоны на 1 позиции.
12. Вводим разрешенную скорость (грузовые 90 , пасс 105)

Скорость и ускорение точки при координатном способе задания движения

Пусть заданы уравнения движения точки (рис. 1.5):

.

Обозначим орты осей координат

. Проведем из начала координат О в движущуюся точку М радиус-вектор . Согласно рис. 1.5

или .

Скорость точки равна производной от радиус-вектора по времени. Найдем эту производную, учитывая, что орты

имеют неизменные модули и направления, т.е. постоянны и могут быть вынесены за знак производной:

.

Построив прямоугольный параллелепипед, ребра которого параллельны осям координат, а диагональ совпадает со скорость

, получим проекции скорости на оси координат , равные алгебраическим величинам отрезков Ма, Мb, Mc.

Тогда разложение скорости на компоненты по осям координат примет вид

.

Сопоставляя обе формулы, определяющие скорость находим

.

(11)

Следовательно, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Пользуясь принятым обозначением производных по времени, имеем

.

(12)

Зная проекции скорости, можно найти её модуль и направление (т.е. углы

, которые вектор образует с координатными осями) по формулам

, .

(13)

Дата добавления: 2015-06-27 ; Просмотров: 196 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Проекции скорости точки на оси координат

1.1.2. КООРДИНАТНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ

При координатном способе задания движения:

То есть и вектор скорости точки, и вектор ее ускорения при координатном способе задания движения определяются через их проекции на координатные оси. А как найти модуль каждого вектора и его направляющие косинусы, повторять, наверное, не стоит.

Отметим, что: уравнения движения точки называют также параметрическими уравнениями траектории точки или годографа ее радиуса-вектора.

Некоторые типовые случаи движения точек приведены на плакате 7к.

Вид уравнений движения и траектории для перечисленных в плакате случаев целесообразно запомнить.

*** Кроме декартовой при решении некоторых специальных задач используются и другие системы координат. В пространстве – это сферическая и цилиндрическая, а на плоскости – полярная системы координат.

В сферической системе координат определяются положение звезд и планет по отношению к Земле, координаты точек (широта и долгота) на земной поверхности; в цилиндрической системе координат определяется положение забоя наклонной скважины по отношению к точке на устье скважины (отклонение от вертикали; азимут отклонения; глубина по вертикали). Полярная система координат хорошо знакома туристам и путешественникам, ориентирующимся по компасу.

В перечисленных системах координат ( плакат 5k ) положение точки определяется иными зависимостями, чем в декартовой системе координат. Однако с помощью этих зависимостей при необходимости очень легко получить уравнения движения точки и в декартовой системе координат. Для этого надо лишь определить проекции радиус-вектора точки на эти оси как функции времени.

Задачи на определение характеристик движения точек в перечисленных системах координат в большинстве программ изучения механики не рассматриваются. Поэтому знать о существовании иных систем координат , и о том, что должно быть задано при их использовании, желательно, а тренироваться в решении задач в этих системах координат нецелесообразно. Научившись хорошо решать задачи в декартовой системе координат, при желании можно быстро научиться решать задачи и в системах координат, описанных выше.

Кинематика поступательного движения.

Иродов И.Е. Механика. (Скачать)
Фриш Том 1. Механика. (Скачать)
Сивухин Д.В. Курс общей физики. Механика.
Савельев И.В. Курс ОБЩЕЙ физики. Механика.
Яворский Б.М., Детлаф А.А. Курс общей физики. Справочник по физике.

Механика — наука о движении и равновесии тел.

Материальная точка – это тело, размеры и форма которого в условиях данной задачи несущественны.

Абсолютно твёрдое тело – это система материальных точек, расстояния между которыми не меняются в процессе движения.

Механическое движение – это изменение положения тела в пространстве с течением времени.

Виды механического движения:
1. Поступательное.
2. Вращение вокруг неподвижной оси.
3. Вращение вокруг неподвижной точки.
4. Плоское движение.
5. Свободное движение.

Поступательное – это такое движение твёрдого тела, при котором любая прямая, связанная с телом, всё время остаётся параллельной своему начальному положению.

Плоское – это такое движение твёрдого тела, при котором каждая его точка движется в плоскости, параллельной некоторой неподвижной (в данной системе отсчёта) плоскости.

Описание механического движения.

Тело отсчёта — это тело, относительно которого задаётся положение данного тела или данной точки.

Система отсчёта — совокупность тела отсчёта, связанной с ним системы координат, и синхронизованных между собой часов.

ДВИЖЕНИЕ ТОЧКИ С ПОЗИЦИЙ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ

Траектория движущейся точки. Движение материальной точки мы рассматриваем в теоретической механике. В этом случае, для описания полного движения точки необходимо знать уравнение её движения т.е.

, где – радиус-вектор точки. Чтобы найти скорость точки надо взять производную от правой части уравнения движения.

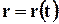
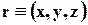
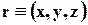
Рассмотрим движение точки в некоторой определённой системе прямоугольных и прямолинейных координат Oxyz, которую условимся называть неподвижной.

Кривая, описываемая последовательными положениями движущейся точки, называется траекторией.

Аналитически движение точки определено, если заданы её координаты x, y, z, как непрерывные функции времени t:

Эти уравнения определяют положение движущейся точки в каждый момент времени t и представляют в параметрической форме уравнение траектории. Если на траектории выбрать точку М, от которой отсчитывать длину дуги s траектории до движущейся точки М, то движение М определяется законом изменения s, как функции времени t:

s = s (t).

Перемещение. Скорость. Пусть М и М¢ – положения движущейся точки, отвечающие соответственно моментам t и t + Dt. Вектор

называется перемещением точки за промежуток времени Dt . Этот вектор с началом в точке М представляет собой хорду, стягивающую положения движущейся точки в моменты t и t + Dt .

Перемещение

разделим на Dt; вектор

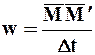
называется средней скоростью точки М за промежуток времени Dt .

Средняя скорость есть вектор, приложенный в точке М и имеющий то же направление, что и перемещение

.

Предел средней скорости, когда Dt стремится к 0, называется скоростью точки М в момент t и обычно обозначается

.

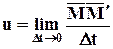
В пределе направление хорды совпадает с направлением касательной к траектории; поэтому скорость u точки М представляет собой вектор, приложенный в точке М и направленный по касательной к траектории в сторону движения.

Положение точки М можно определить вектором

, выходящим из начала координат О. Перемещение за промежуток времени Dt равно приращению вектора :

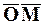
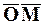
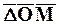
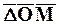
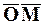
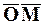
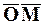
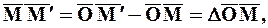
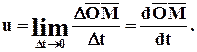
Таким образом, скорость движущейся точки равна производной по времени от радиуса-вектора движущейся точки и представляет собой вектор, приложенный в движущейся точке.

Проекции скорости на оси координат. Пусть x, y, z координаты точки М, а x + Dx, y +Dy, z +Dz – координаты точки

. Проекции перемещения на оси координат будут соответственно равны Dx, Dy, Dz; проекции средней скорости w будут

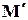
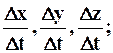
отсюда проекции истинной скорости u на оси координат Oxyz будут пределами предыдущих выражений при Dt® 0, или

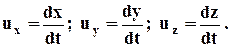
Теорема. Проекции скорости на прямоугольные оси равны первым производным по времени от соответствующих координат движущейся точки.

Так как оси Oxyz ортогональны, величина скорости определится через проекции формулой:

.

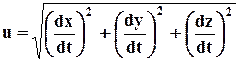
Если через s обозначить длину дуги траектории, отсчитываемой от неподвижной точки, то

.

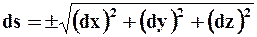
Следовательно, алгебраическая величина скорости будет определяться формулой

.

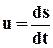
При этом, если u положительна, то скорость направлена в сторону возрастающих значений s. Движение называется равномерным, если величина скорости постоянна. Тогда

Допустим, что s есть значение s для начального момента времени t = 0; тогда, интегрируя предыдущее выражение, получаем: s = s + at.

То есть, в равномерном движении пройденные пути пропорциональны времени. Величина скорости равна пути, пройденному в равномерном движении за единицу времени.

Теорема о проекции скорости. Возьмём ось х за траекторию движения (если движение прямолинейное). Значит s = х, и уравнение движения имеет вид: x = f(t). Алгебраическая величина скорости точки, движущейся по оси х, представляется формулой

v = dx/dt = f¢(t).

Но, при движении точки в пространстве, dx/dt есть проекция её скорости на ось х; в то же время эта величина равна скорости ортогональной проекции М₁ точки М на ось х, так как х есть абсцисса точки М₁.

Следовательно, если спроектировать на неподвижную ось движущуюся точку и её скорость, то проекция скорости будет равна скорости проекции.

Дата добавления: 2016-01-09 ; просмотров: 394 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ