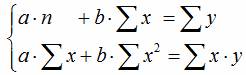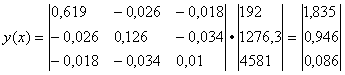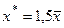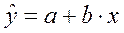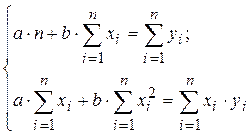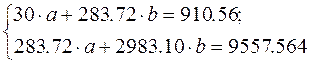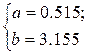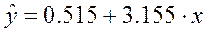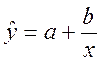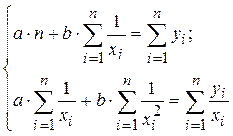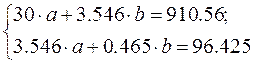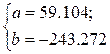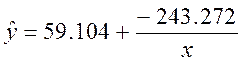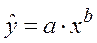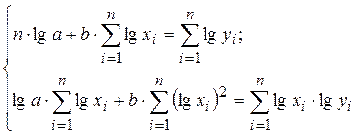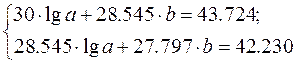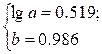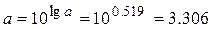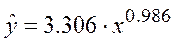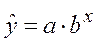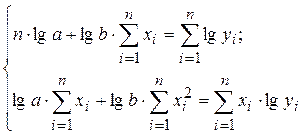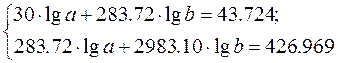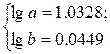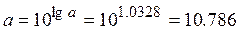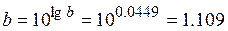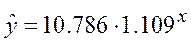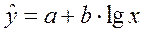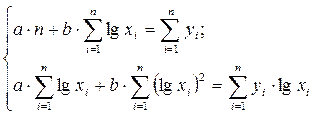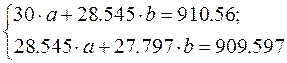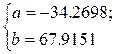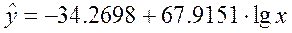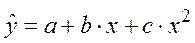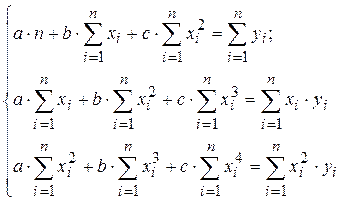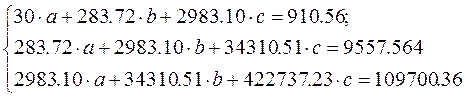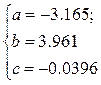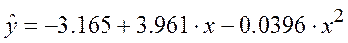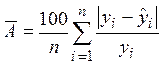Получено уравнение регрессии

Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии:

. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Уравнение множественной регрессии

Назначение сервиса . С помощью онлайн-калькулятора можно найти следующие показатели:

• уравнение множественной регрессии, матрица парных коэффициентов корреляции, средние коэффициенты эластичности для линейной регрессии;
• множественный коэффициент детерминации, доверительные интервалы для индивидуального и среднего значения результативного признака;

Кроме этого проводится проверка на автокорреляцию остатков и гетероскедастичность.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Отбор факторов обычно осуществляется в два этапа:

1. теоретический анализ взаимосвязи результата и круга факторов, которые оказывают на него существенное влияние;
2. количественная оценка взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится к анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Научно обоснованное решение задач подобного вида также осуществляется с помощью дисперсионного анализа – однофакторного, если проверяется существенность влияния того или иного фактора на рассматриваемый признак, или многофакторного в случае изучения влияния на него комбинации факторов.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между фактором и результатом должен быть существенным).
3. Факторы не должны быть сильно коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность – тесная линейная связь между факторами.

Пример . Постройте регрессионную модель с 2-мя объясняющими переменными (множественная регрессия). Определите теоретическое уравнение множественной регрессии. Оцените адекватность построенной модели.
Решение.
К исходной матрице X добавим единичный столбец, получив новую матрицу X

1	5	14.5
1	12	18
1	6	12
1	7	13
1	8	14

Матрица Y

9

13

16

14

21

Транспонируем матрицу X, получаем X T :

1	1	1	1	1
5	12	6	7	8
14.5	18	12	13	14

Умножаем матрицы, X T X =

5 38 71,5 38 318 563,5 71,5 563,5 1043,25

В матрице, (X T X) число 5, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X

Умножаем матрицы, X T Y =

73 563 1032,5

Находим обратную матрицу (X T X) -1

13.99	0.64	-1.3
0.64	0.1	-0.0988
-1.3	-0.0988	0.14

Вектор оценок коэффициентов регрессии равен

(X T X) -1 X T Y = y(x) =

13,99 0,64 -1,3 0,64 0,1 -0,0988 -1,3 -0,0988 0,14

*

73 563 1032,5

=

34,66 1,97 -2,45

Год	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X1	3,5	2,8	6,3	4,5	3,1	1,5	7,6	6,7	4,2	2,7	4,5	3,5	5,0	2,3	2,8
X2	4,5	3,0	3,1	3,8	3,8	1,1	2,3	3,6	7,5	8,0	3,9	4,7	6,1	6,9	3,5
Y	9,0	6,0	8,9	9,0	7,1	3,2	6,5	9,1	14,6	11,9	9,2	8,8	12,0	12,5	5,7

Решение. Подготовим данные для вставки из MS Excel (как транспонировать таблицу для сервиса см. Задание №2) .

Включаем в отчет: Проверка общего качества уравнения множественной регрессии (F-статистика. Критерий Фишера, Проверка на наличие автокорреляции),

После нажатия на кнопку Дале получаем готовое решение.
Уравнение регрессии (оценка уравнения регрессии):
Y = 0.2706 + 0.5257X₁ + 1.4798X₂
Скачать.

Качество построенного уравнения регрессии проверяется с помощью критерия Фишера (п. 6 отчета).

Пример №3 .
В таблице представлены данные о ВВП, объемах потребления и инвестициях некоторых стран.

ВВП	16331,97	16763,35	17492,22	18473,83	19187,64	20066,25	21281,78	22326,86	23125,90
Потребление в текущих ценах	771,92	814,28	735,60	788,54	853,62	900,39	999,55	1076,37	1117,51
Инвестиции в текущих ценах	176,64	173,15	151,96	171,62	192,26	198,71	227,17	259,07	259,85

Решение:
Для проверки полученных расчетов используем инструменты Microsoft Excel «Анализ данных» (см. пример).

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3.9	3.9	3.7	4	3.8	4.8	5.4	4.4	5.3	6.8	6	6.4	6.8	7.2	8	8.2	8.1	8.5	9.6	9
10	14	15	16	17	19	19	20	20	20	21	22	22	25	28	29	30	31	32	36

Умножаем матрицы, (X T X)

Умножаем матрицы, (X T Y)

Находим определитель det(X T X) T = 139940.08
Находим обратную матрицу (X T X) -1

Вектор оценок коэффициентов регрессии равен s = (X T X) -1 X T Y =

Уравнение регрессии
Y = 1.8353 + 0.9459X ₁ + 0.0856X ₂
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y – X*s

0.62
0.28
0.38
0.01
0.11
-1
-0.57
0.29
-0.56
0.02
-0.31
1.23
-1.15
0.21
0.2
-0.07
-0.07
-0.53
0.34
0.57

se 2 = (Y – X*s) T (Y – X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

k(x) = 0.36

0,619 -0,0262 -0,0183 -0,0262 0,126 -0,0338 -0,0183 -0,0338 0,0102

=

0,222 -0,00939 -0,00654 -0,00939 0,0452 -0,0121 -0,00654 -0,0121 0,00366

Дисперсии параметров модели определяются соотношением S 2 _i = K_ii, т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции (от 0 до 1)

Связь между признаком Y факторами X сильная
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора х_i при неизменном уровне других факторов определяются по стандартной формуле линейного коэффициента корреляции – последовательно берутся пары yx1,yx2. , x1x2, x1x3.. и так далее и для каждой пары находится коэффициент корреляции

Коэффициент детерминации
R 2 = 0.97 2 = 0.95, т.е. в 95% случаев изменения х приводят к изменению y. Другими словами – точность подбора уравнения регрессии – высокая

Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл: T_табл (n-m-1;a) = (17;0.05) = 1.74
Поскольку Tнабл Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

Построение парной регрессионной модели

Рекомендации к решению контрольной работы.

Статистические данные по экономике можно получить на странице Россия в цифрах.
После определения зависимой и объясняющих переменных можно воспользоваться сервисом Множественная регрессия. Регрессионную модель с 2-мя объясняющими переменными можно построить используя матричный метод нахождения параметров уравнения регрессии или метод Крамера для нахождения параметров уравнения регрессии.

Пример №3 . Исследуется зависимость размера дивидендов y акций группы компаний от доходности акций x₁, дохода компании x₂ и объема инвестиций в расширение и модернизацию производства x₃. Исходные данные представлены выборкой объема n=50.

Тема II. Множественная линейная регрессия
1. Постройте выборочную множественную линейную регрессию показателя на все указанные факторы. Запишите полученное уравнение, дайте ему экономическую интерпретацию.
2. Определите коэффициент детерминации, дайте ему интерпретацию. Вычислите среднюю абсолютную ошибку аппроксимации

и дайте ей интерпретацию.
3. Проверьте статистическую значимость каждого из коэффициентов и всего уравнения в целом.
4. Постройте диаграмму остатков.
5. Постройте доверительные интервалы коэффициентов. Для статистически значимых коэффициентов дайте интерпретации доверительных интервалов.
6. Постройте точечный прогноз значения показателя y при значениях факторов, на 50% превышающих их средние значения.
7. Постройте доверительный интервал прогноза, дайте ему экономическую интерпретацию.
8. Постройте матрицу коэффициентов выборочной корреляции между показателем и факторами. Сделайте вывод о наличии проблемы мультиколлинеарности.
9. Оцените полученные результаты — сделайте выводы о качестве построенной модели, влиянии рассматриваемых факторов на показатель.

Задание к контрольной работе по курсу «Эконометрика»

На основе данных выданных преподавателем необходимо:

1. Определить параметры следующих уравнений регрессии:

г) показательного (экспоненциального);

2. Оценить качество каждой модели взаимосвязи с помощью средней ошибки аппроксимации и показателя детерминации.

3. На основании результатов, полученных в пункте 2, выбрать уравнение регрессии, наилучшим образом описывающее взаимосвязь между фактором х и результативным признаком у.

4. По выбранной модели взаимосвязи сделать точечный прогноз для значения фактора равного

.

Определение параметров уравнений регрессии

Линейное уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Построенное уравнение регрессии:

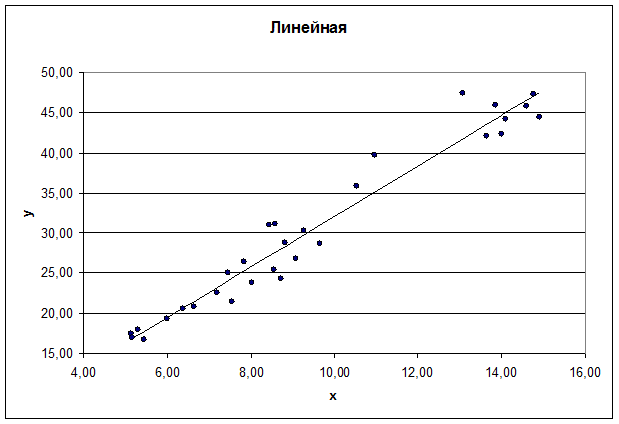
Рис. 1. График линейного уравнения регрессии

Гиперболическое уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Построенное уравнение регрессии:

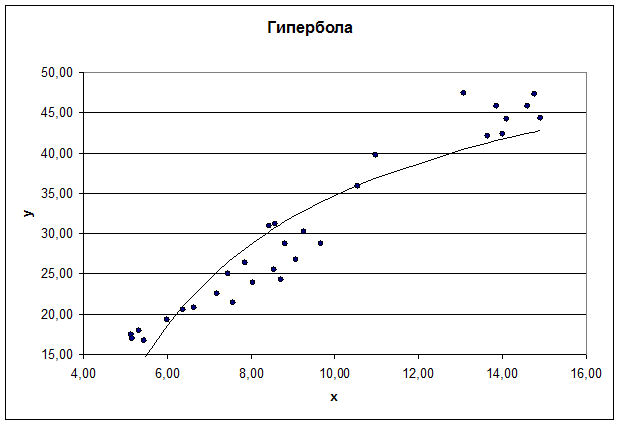
Рис. 2. График гиперболического уравнения регрессии

Степенное уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Построенное уравнение регрессии:

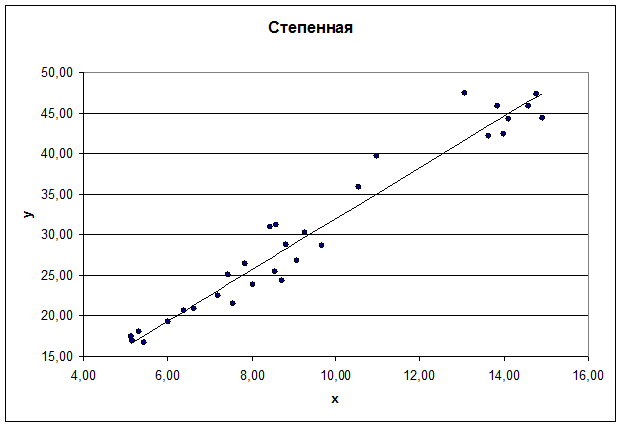
Рис. 3. График степенного уравнения регрессии

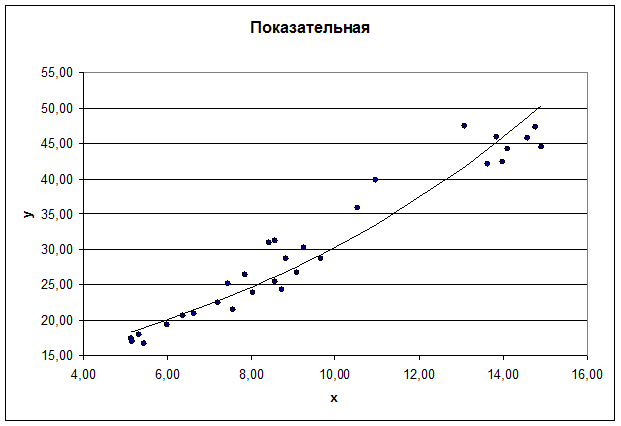
Показательное уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

;

Построенное уравнение регрессии:

Рис. 4. График показательного уравнения регрессии

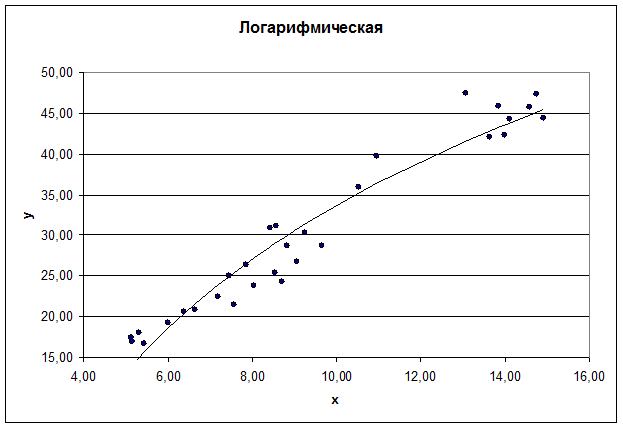
Логарифмическое уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Построенное уравнение регрессии:

Рис. 5. График логарифмического уравнения регрессии

Параболическое уравнение регрессии

Система нормальных уравнений в общем виде:

Система нормальных уравнений с вычисленными коэффициентами

Построенное уравнение регрессии:

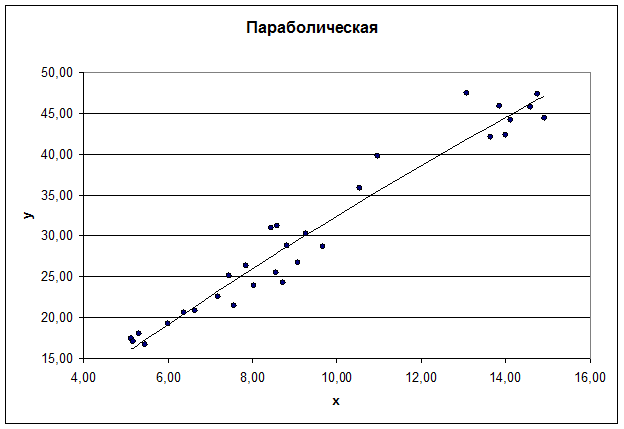
Рис. 6. График параболического уравнения регрессии

Оценка качества построенных уравнений регрессии

Средняя ошибка аппроксимации:

Название	Уравнение	A, %	R 2
Линейная		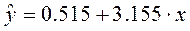5.765	0.950
Гипербола		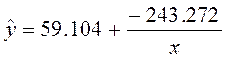11.839	0.867
Степенная		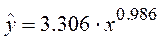5.758	0.951
Показательная		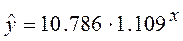7.152	0.921
Логарифмическая		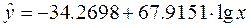7.862	0.934
Параболическая		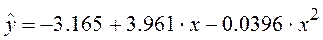5.904	0.952

Выбор уравнения регрессии

На основании результатов, полученных в пункте 2, можно сделать вывод, что наиболее подходящими для описания взаимосвязи между результативной переменной у и фактором х являются функции: параболическая, степенная и линейная, поскольку эти функции имеют наиболее близкие к единице значения показателя детерминации. Для дальнейших вычислений выберем линейную функцию, как наиболее простую, и в то же самое время не уступающую по качеству двум другим выделенным ранее.

Уравнения линейной регрессии (стр. 1 из 3)

Министерство образования и науки РФ

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Филиал в г. Туле

по дисциплине «Эконометрика»

По предприятиям легкой промышленности получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х, млн. руб.) табл. 1.

Х	33	17	23	17	36	25	39	20	13	12
Y	43	27	32	29	45	35	47	32	22	24

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора Х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения Y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

1. Линейная модель имеет вид:

Параметры уравнения линейной регрессии найдем по формулам

Расчет значения параметров представлен в табл. 2.

1 43 33 1419 1089 42,236 0,764 0,584 90,25 88,36 0,018 2 27 17 459 289 27,692 -0,692 0,479 42,25 43,56 0,026 3 32 23 736 529 33,146 -1,146 1,313 0,25 2,56 0,036 4 29 17 493 289 27,692 1,308 1,711 42,25 21,16 0,045 5 45 36 1620 1296 44,963 0,037 0,001 156,25 129,96 0,001 6 35 25 875 625 34,964 0,036 0,001 2,25 1,96 0,001 7 47 39 1833 1521 47,69 -0,69 0,476 240,25 179,56 0,015 8 32 20 640 400 30,419 1,581 2,500 12,25 2,56 0,049 9 22 13 286 169 24,056 -2,056 4,227 110,25 134,56 0,093 10 24 12 288 144 23,147 0,853 0,728 132,25 92,16 0,036 ∑ 336 235 8649 6351 12,020 828,5 696,4 0,32 Средн. 33,6 23,5 864,9 635,1

Определим параметры линейной модели

Линейная модель имеет вид

2. Вычислим остатки

Расчеты представлены в табл. 2.

Рис. 1. График остатков ε.

3. Проверим выполнение предпосылок МНК на основе критерия Дарбина-Уотсона.

0,584 2,120 0,479 0,206 1,313 6,022 1,711 1,615 0,001 0,000 0,001 0,527 0,476 5,157 2,500 13,228 4,227 2,462 0,728 31,337 12,020

d1=0,88; d2=1,32 для α=0,05, n=10, k=1.

значит, ряд остатков не коррелирован.

4. Осуществим проверку значимости параметров уравнения на основе t-критерия Стьюдента. (α=0,05).

5. Найдем коэффициент корреляции по формуле

Расчеты произведем в табл. 2.

Коэффициент детерминации найдем по формуле

Проверим значимость уравнения регрессии с помощью F-критерия Фишера

Fтаб=5,32, т.к. k1=1, k2=8, α=0,05

т.к. F значительно больше Fтабл, то можно сделать вывод, что уравнение регрессии с вероятностью 95% статистически значимо.

Оценим точность модели на основе использования средней относительной ошибки аппроксимации.

Расчеты произведены в табл. 2.

значит, линейную модель можно считать точной, т.к. Е

Уравнение регрессии

Определение и уравнение регрессии

Чаще всего регрессия задается уравнением, которое показывает зависимость между двумя группами числовых переменных. Уравнения бывают двух видов: линейные и нелинейные.

Регрессия бывает двух видов: парная (или двухфакторная) и множественная (или многофакторная). Такие регрессии отличаются друг от друга видом уравнения и количестве независимых переменных. Уравнения парной регрессии относятся к уравнениям регрессии первого порядка, а уравнения множественной регрессии — к нелинейным уравнениям регрессии.

Параметры уравнения линейной регрессии

находятся методом наименьших квадратов из системы нормальных уравнений

Примеры решения задач

Задание

Пусть задана зависимость между выработкой продукции на одного работника и удельного веса рабочих высокой квалификации:

Определите теоретическое уравнение парной регрессии.

Решение Выборка состоит из 10 предприятий отрасли, то есть . Уравнение парной регрессии будем искать в виде:

Для определения параметров модели, будем использовать метод наименьших квадратов. Система нормальных уравнений для определения неизвестных величин

и имеет вид:

Вычислим необходимые значения, для этого построим следующую таблицу:

Составляем систему нормальных уравнений:

Решая полученную систему линейных уравнений любым из известных методов, будем иметь:

Тогда искомое уравнение

Ответ

Задание

Имеются следующие данные разных стран об индексе розничных цен на продукты питания () и индексе промышленного производства ():

Необходимо для характеристики зависимости

от рассчитать параметры следующих функций: а) линейной; б) степенной; в) равносторонней гиперболы. Решение а) для построения линейной регрессии заполним таблицу:

Для нахождения параметров регрессии, решаем систему нормальных уравнений (1):

То есть уравнение линейной регрессии

.

б) Степенная регрессия имеет вид

.

Прологарифмируем это равенство десятичным логарифмом:

По способу наименьших квадратов строим систему нормальных уравнений для определения параметров регрессии:

Построим расчетную таблицу:

Подставляем в систему:

Решая полученную систему, будем иметь:

Тогда искомое уравнение

в) Уравнение равносторонней гиперболы

.

Для определения параметров этого уравнения используется система нормальных уравнений:

Составим таблицу расчетных данных:

Получаем следующую систему нормальных уравнений:

Решая записанную систему, получаем следующие значения параметров регрессии:

Получено уравнение регрессии

Значение свободного члена уравнения регрессии в натуральном масштабе находим из уравнения [c.181]

Это означает, что с ростом фактора а , на одну сигму при неизменной численности занятых затраты на продукцию увеличиваются в среднем на 0,5 сигмы. Так как /3, 1. Преобразование в этих случаях заключается во взятии натурального логарифма от Y, а и X. Получающееся уравнение регрессии будет выглядеть так [c.295]

Результаты полученных средних значений скорости чтения позволили построить уравнение регрессии (в натуральных переменных) следующего вида [c.125]

Применение в практических целях уравнения множественной регрессии в стандартизованном масштабе затруднительно, поэтому уравнение множественной регрессии следует перевести в натуральный масштаб. Перевод коэффициентов множественной регрессии из стандартизованного масштаба в натуральный производится по формуле [c.180]

Отсюда уравнение множественной регрессии в натуральном масштабе для уровня торгово-управленческих расходов I группы управлений имеет вид [c.181]

Найдите уравнение множественной регрессии в стандартизованном и натуральном масштабе. [c.88]

Постройте уравнение линейной регрессии, отражающее зависимость между объемом реализации продукции (в натуральных единицах) и ценой за единицу продукции, по следующим данным [c.437]

Теоретическая линия регрессии может быть рассчитана в этом случае по результатам отдельных наблюдений. Для решения системы нормальных уравнений нам потребуются те же данные х, у, ху и хг. Рассмотрим пример расчета. Мы располагаем данными об объеме производства цемента и объеме основных производственных фондов в 1958 г. Ставится задача исследовать зависимость между объемом производства цемента (в натуральном выражении) и объемом основных фондов. [c.73]

Подставив эти значения в выражение (30), получим уравнение множественной регрессии улова рыбы в натуральном масштабе [c.130]

Для практического использования полученные зависимости должны быть выражены в натуральном масштабе. Уравнение множественной регрессии в натуральном масштабе имеет вид [c.126]

Дли более удобного практического использования приведенной формулы полученные зависимости переводим в натуральный масштаб. С этой целью проводим ряд преобразований, смысл которых заключается в выделении соотношений между о 0, ор, O M, оМж.б и соответствующими р и Ь (принятыми в начальном уравнении множественной регрессии). [c.150]

Кроме проверки значимости всей модели, необходимо провести проверки значимости коэффициентов регрессии по /-критерию Стюдента. Минимальное значение коэффициента регрессии Ьг должно соответствовать условию bifob- t, где bi — значение коэффициента уравнения регрессии в натуральном масштабе при i-ц факторном признаке аь. — средняя квадратическая ошибка каждого коэффициента. [c.181]

Интересно также выявить, как изменяется исследуемый показатель при изменении факторов, измеряемых в натуральных единицах. От уравнения регресии в стандартизованном масштабе к уравнению регрессии в натуральном масштабе можно перейти следующим образом. Пусть в ре зультате расчетов получено уравнение регрессии [c.130]