Плоскость перпендикулярная плоскости проекции

Плоскость перпендикулярная плоскости проекции

Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими.

Горизонтально-проецирующая плоскость δ(δ₁)⊥ П₁ – плоскость, перпендикулярная горизонтальной плоскости проекций П₁ (рис. 35, 36). Горизонтально-проецирующая плоскость задается горизонтальным следом плоскости δ₁ , который является геометрическим местом горизонтальных проекций всех точек, принадлежащих данной плоскости.

Углы наклона горизонтально-проецирующей плоскости к П₂ и П₃ проецируются на горизонтальную плоскость проекций в натуральную величину

Фронтально-проецирующая плоскость γ(γ₂)⊥ П₂ – плоскость, перпендикулярная фронтальной плоскости проекций П₂, задается фронтальным следом плоскости γ₂ (рис. 37, 38).

Проекции всех линий и точек, лежащих во фронтально-проецирующей плоскости, совпадают с фронтальным следом этой плоскости. Углы наклона фронтально-проецирующей плоскости к П₁ и П₃ проецируются на фронтальную плоскость проекций в натуральную величину.

Профильно-проецирующая плоскость σ(σ₃)⊥ П₃ – плоскость, перпендикулярная профильной плоскости проекций П₃ , задается профильным следом плоскости σ₃ (рис. 39, 40).

Прямая и плоскость

Взаимно перпендикулярные прямая и плоскость могут быть построены на эпюре Монжа из условия перпендикулярности прямой к двум пересекающимся прямым, принадлежащим этой плоскости.

Если в плоскости взять пересекающиеся горизонталь и фронталь, то появляется возможность воспользоваться теоремой о проецировании прямого угла.

Построение прямой перпендикулярной к плоскости общего положения заданной треугольником.

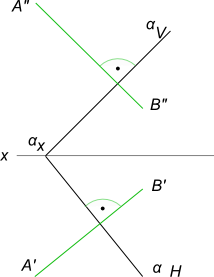
Через точку A провести прямую перпендикулярную плоскости α, заданной следами или из точки A опустить перпендикуляр AB на плоскость α, заданную следами.

Для решения этой задачи достаточно из A` провести горизонтальную проекцию (A`B`)⊥α_H, а из A” – ее фронтальную проекцию (A”B”)⊥α_V.

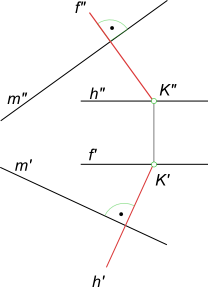
Через данную точку K провести плоскость α, перпендикулярную к заданной прямой m

Плоскость α задаем пересекающимися в точке K прямыми – горизонталью h и фронталью f перпендикулярными горизонтальной и фронтальной проекциям прямой соответственно.

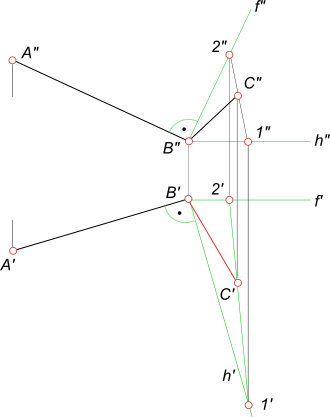
Найти недостающую проекцию стороны BC угла ABC.

Через сторону BC угла ABC провести плоскость α ⊥(A”B”). В плоскости α, заданной горизонталью h и фронталью f, проводим через точку C прямую 12. Сначала это возможно сделать на фронтальной, затем и на горизонтальной плоскости проекций.

Через данную точку K провести плоскость δ, перпендикулярную двум заданным плоскостям α и β

Две заданные плоскости α и β пересекаются либо по собственной прямой либо по несобственной. Сначала находим их линию пересечения, а затем проводим через точку K искомую плоскость δ, задавая ее горизонталью h и фронталью f. Затем плоскость δ выражаем следами.

Если Вы искали как провести плоскость через прямую перпендикулярную плоскости заданной параллельными прямыми то следует смотреть: Взаимно перпендикулярные плоскости;

Плоскость перпендикулярная плоскости проекции

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На основании теоремы о проекциях прямого угла можно получить условие перпендикулярности прямой общего положения и плоскости общего положения:

Если прямая a перпендикулярна плоскости α(ABC), то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Например, при построении прямой a, перпендикулярной плоскости α(ABC) (рис. 125, а), в плоскости строятся линии уровня – горизонталь и фронталь, затем через произвольную точку в плоскости, в данном случае точку K(h×f), строится прямая, горизонтальная проекция которой перпендикулярна горизонтальной проекции горизонтали плоскости α(ABC), а фронтальная проекция – фронтальной проекции фронтали плоскости.

б – построение плоскости, перпендикулярной прямой:

Аналогично решается задача о построении плоскости, перпендикулярной прямой общего положения (рис. 125, б)

Если плоскость проецирующая, проекции линий уровня совпадают со следом плоскости, перпендикулярность устанавливается по отношению к следу плоскости. Горизонтальная проекция перпендикуляра к горизонтально-проецирующей плоскости строится перпендикулярно горизонтальному следу плоскости (рис. 126, а). Прямая, перпендикулярная горизонтально-проецирующей плоскости, занимает положение горизонтальной линии уровня.

Аналогично, фронтальная проекция перпендикуляра к фронтально-проецирующей плоскости строится перпендикулярно фронтальному следу плоскости (рис. 126, б). Прямая, перпендикулярная фронтально-проецирующей плоскости, занимает положение фронтали.

На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П₁ в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П₂ – если одна из них фронталь (рис. 123, а).

Условие перпендикулярности скрещивающихся прямых (рис. 123, б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.

Плоскость перпендикулярная плоскости проекции

Контрольные задания по теме: Рабочая тетрадь задача 44, задача 45

Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.

Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.

Рисунок 28

Сторона ВС прямого угла АВС, изображенного на рисунке 28, параллельна плоскости П 1 . Следовательно, проекция угла АВС на эту плоскость будет представлять прямой угол А 1 В 1 С 1 =90.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. При построении перпендикуляра из множества прямых принадлежащих плоскости, выбирают прямые уровня – горизонталь и фронталь. В этом случае горизонтальную проекцию перпендикуляра проводят перпендикулярно горизонтали, а фронтальную -перпендикулярно фронтали. На примере, изображенном на рисунке 29, показано построение перпендикуляра к плоскости, заданной треугольником АВС, из точки К. Для этого сначала проводим горизонталь и фронталь в плоскости. Затем из фронтальной проекции точки К проводим перпендикуляр к фронтальной проекции фронтали, а из горизонтальной проекции точки – перпендикуляр к горизонтальной проекции горизонтали. Затем строим точку пересечения данного перпендикуляра с плоскостью при помощи вспомогательной секущей плоскости Σ. Искомая точка – F. Таким образом, полученный отрезок КF является перпендикуляром к плоскости АВС.

Рисунок 29

На рисунке 29 изображено построение перпендикуляра КF к плоскости АВС.

Две плоскости перпендикулярны, если прямая, лежащая в одной плоскости, перпендикулярна двум пересекающимся прямым другой плоскости. Построение плоскости перпендикулярной данной плоскости АВС показано на рисунке 30. Через точку М проводится прямая МN, перпендикулярная плоскости АВС. Горизонтальная проекция этой прямой перпендикулярна АС, так как АС является горизонталью, а фронтальная проекция перпендикулярна АВ, так как АВ – фронталь. Затем через точку М проводится произвольная прямая EF. Таким образом, плоскость перпендикулярна АВС и задана двумя пересекающимися прямыми EF и MN.

Рисунок 30

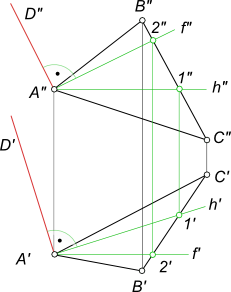
Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.

Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.

Проводим перпендикуляр к одному из концов отрезка на горизонтальной плоскости. Откладываем на нем разность высот (ZA-ZB) концов отрезка и достраиваем прямоугольный треугольник. Гипотенуза его является натуральной величиной отрезка, а угол между натуральной величиной и проекцией отрезка – натуральной величиной угла наклона отрезка к плоскости П 1 . Порядок построений на фронтальной плоскости тот же самый. По перпендикуляру откладываем разность глубин концов отрезка (YA-YB). Полученный угол между натуральной величиной отрезка и его фронтальной проекцией – это угол наклона отрезка к плоскости П 2 .

Рисунок 31

1. Сформулируйте теорему о свойстве прямого угла.

2. В каком случае прямая перпендикулярна плоскости?

3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства?

4. Для чего применяется способ прямоугольного треугольника?

5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Взаимно перпендикулярные плоскости имеют место быть, когда одна из них содержит прямую перпендикулярную к другой плоскости.

Для построения плоскости α перпендикулярной плоскости β намечаем алгоритм решения: – проводим прямую m перпендикулярную плоскости β; – заключаем прямую m в плоскость α.

Через прямую a провести плоскость α, перпендикулярную к плоскости β, заданной параллельными прямыми b и d

Выполняя первую строку алгоритма: – находим направление проекций перпендикуляра к плоскости β, построив для этого горизонталь h и фронталь f плоскости β; Выполняя вторую строку алгоритма: – из проекций произвольной точки A, взятой на прямой a, проводим проекции перпендикуляра m`⊥h` m”⊥f”. Выполнив алгоритм полностью имеем: m ⊥ β ⇒ α ⊥ β.

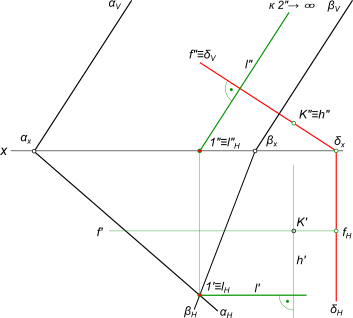
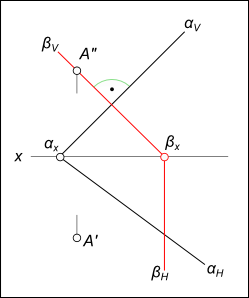
Через данную точку A провести фронтально проецирующую плоскость β перпендикулярную к плоскости α заданной следами.

Фронтально проецирующая плоскость β перпендикулярная к плоскости α должна содержать прямую m перпендикулярную ей: – m” ⊥ α_V; – m` ⊥ α_H; – находим следы прямой mH и mV; – проводим следы искомой плоскости через следы mH и mV: – фронтальный след β_V, он совпадает с m” и находим β_x; – горизонтальный след β_H ⊥ x.

Плоскость перпендикулярная плоскости проекции

Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.

Рисунок 8

а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

Рисунок 9

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

Рисунок 10

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

Рисунок 11

Горизонтальная проекция фронтали параллельна оси Х, а угол β – угол наклона фронтали к горизонтальной плоскости проекций; f₂ // П2, β= Ð f1 П1.

Профильная прямая – это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β – соответственно, углы наклона прямой к плоскостям П 1 и П2.

Рисунок 12.

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

Рисунок 13

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

а) три точки, не лежащие на одной прямой;

Рисунок 14

б) прямая и точка, не лежащая на ней;

Рисунок 15

в) две параллельные прямые;

Рисунок 16

г) две пересекающиеся прямые;

Рисунок 17

д) плоская фигура (многоугольник, круг и т.д.).

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Рисунок 18

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

Рисунок 19

На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) – параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.

Рисунок 20

1. Как образуется комплексный чертеж прямой линии?

2. Прямые какого положения вы знаете?

3. Назовите прямые уровня.

4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?

5. Перечислите способы задания плоскости.

6. Дайте определение плоскости общего положения.

7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Плоскость перпендикулярная плоскости проекции

СПОСОБ ПРОЕЦИРОВАНИЯ НА ДОПОЛНИТЕЛЬНУЮ ПЛОСКОСТЬ

Этот способ широко применяют в практике выполнения чертежей. Сущность способа проецирования на дополнительную плоскость проекций заключается в следующем: положение точек, линий, плоских фигур, геометрических тел в пространстве не изменяется, а данная система плоскостей проекций дополняется плоскостями, расположенными к П 1 или П 2 , или друг к другу под прямым углом.

Каждая новая плоскость выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение наиболее удобное для выполнения требуемого построения.

Рис. 6.4.

На рис.6.4 показано построение проекции точки А на дополнительную плоскость П 4 , перпендикулярную П 1 . П 1 &#199 П 2 = х ; П 1 &#199 П 4 = х 1 . Перпендикуляры, опущенные из точки А на плоскости П 1 , П 2 , П 4 , определят проекции А 1 , А 2 , А 4 . Из чертежа на рис.6.4а видно, что расстояние от дополнительной проекции А 4 точки до оси х 1 равно расстоянию от А 2 до оси х , т.е. координате Z . Следовательно, можно сделать вывод, что расстояние от дополнительной проекции до новой оси равно той координате точки, которая отсутствует в плоскости, перпендикулярной к дополнительной.

Совместив далее П 2 и П 4 с плоскостью П 1 вращением П 2 вокруг оси х и П 4 вокруг х 1 , получим комплексный чертеж точки А (рис.6.46). При наличии на чертеже двух основных проекций А 1 и А 2 , дополнительную проекцию А 4 построим следующим образом. Через А 1 проведем линию связи, перпендикулярную х 1 . Отложив расстояние А X1 А 4 , равное координате Z точки А , получим проекцию А 4 .

При введении дополнительной плоскости проекций, перпендикулярной П 2 , вдоль линии связи откладываем ту координату точки, которая отсутствует в плоскости П 2 , т.е. координату Y . Если П 4 &#94 А 3 , то вдоль линии связи откладываем координату X .

Способом проецирования на дополнительную плоскость можно определить натуральную величину отрезка прямой. Для этого дополнительную плоскость располагают параллельно отрезку.

На рис.6.5 дополнительная плоскость П 4 перпендикулярна П 3 . Новая ось х 1 должна быть расположена относительно проекции прямой на плоскости, перпендикулярной к дополнительной, так же, как новая плоскость относительно прямой. В данном случае х 1 &#189&#189 А 2 В 2 . Вдоль линии связи от оси х 1 откладываем ту координату точек А и В , которая отсутствует в плоскости П 2 (плоскость, перпендикулярная к дополнительной),т.е. координату Y .

Рис. 6.5.

Таким образом, прямая общего положения в системе плоскостей проекций П 1 &#94 П 2 преобразована в прямую уровня в системе П 4 &#94 П 2 . Отрезок АВ на П 4 спроецировался без искажения. Без искажения проецировался и угол наклона прямой к плоскости П 2 .

При решении некоторых задач приходится выполнять преобразование прямой уровня в проецирующую (рис.6.6). В этом случае дополнительная плоскость должна быть перпендикулярна прямой. Так как АВ &#189&#189 П 1 , то П 4 должна быть перпендикулярна П 1 . Тогда новая ось х 1 &#94 А 1 В 1 . Вдоль линии связи откладываем координату Z .

Рис. 6.6.

Часто бывает необходимо плоскость общего положения преобразовать в проецирующую. Для того чтобы плоскость преобразовать в проецирующую следует любую прямую, принадлежащую плоскости, преобразовать в проецирующую. Для преобразования лучше выбрать прямую уровня, так как тогда уменьшается количество преобразований. На рис.6.7 преобразование треугольника АВС в проецирующий выполнено с помощью горизонтали h , проведенной через точку А . Новая плоскость проекций П 4 в этом случае должна быть перпендикулярна горизонтали h (ось х 1 перпендикулярна h 1 ) и, соответственно, перпендикулярна плоскости проекций П 1 .

Рис. 6.7. Рис. 6.8.

После преобразования плоскости общего положения в проецирующую, можно найти натуральную величину плоской фигуры, преобразовав ее в плоскость уровня. На рис.6.8 плоскость &#83 , заданная треугольником АВС , перпендикулярна фронтальной плоскости проекций. В этом случае новая плоскость П 4 , параллельная &#83 , должна быть перпендикулярна П 2 . Ось х 1 – параллельна &#83 1 . Проекция А 4 В 4 С 4 является натуральной величиной заданного треугольника.

Таким образом, последовательным введением двух дополнительных плоскостей проекций может быть определена натуральная величина плоской фигуры, принадлежащей плоскости общего положения.

Плоскость перпендикулярная плоскости проекции

Плоскость можно рассматривать как результат перемещения прямолинейной образующей l , все время оставаясь параллельной прямой b , вдоль направляющей а . При этом а является также прямой (рис.3.5). Определитель плоскости записывается следующим образом: &#70 ( l , а )[ l &#189&#189 b ].

Рис. 3.5.

3.4.1.Задание плоскости на чертеже

Множество элементов плоскости изобразить на чертеже нельзя. Поэтому плоскость принято изображать геометрическими элементами, лежащими в плоскости.

Задание плоскости тремя точками.
Три точки, не лежащие на одной прямой, задают плоскость (рис.3.6а). Любая четвертая, пятая и т.д. точки, взятые произвольно на чертеже, как правило, не принадлежат заданной плоскости. Определитель: &#83 ( A , B , C ).

Рис. 3.6-a Рис. 3.6-б

Задание плоскости прямой и точкой вне этой прямой.
Если две точки плоскости соединить прямой, то получим задание плоскости прямой и точкой (рис.3.6-б). Всякий дополнительный элемент (точка, прямая), взятый произвольно, как правило, не будет принадлежать этой плоскости. Определитель: &#83 ( A , b )[ A &#203 b ].

Задание плоскости двумя пересекающимися прямыми.
Две пересекающиеся прямые определяют плоскость (рис.3.6-в). Определитель: &#83 ( A , b )[ A &#203 b ].

В ряде случаев плоскость удобно задавать двумя пересекающимися прямыми уровня: горизонталью и фронталью (рис.3.6-г).

Рис. 3.6-в Рис. 3.6-г

Задание плоскости двумя параллельными прямыми.
Так как параллельные прямые можно рассматривать как пересекающиеся в несобственной точке, то они также будут определять плоскость (рис.3.6-д). Определитель: &#83 ( a &#189&#189 b ).

Задание плоскости плоской фигурой (отсек плоскости).
Любая плоская фигура, например треугольник, задает плоскость (рис.3.6-е). Плоская фигура придает большую наглядность изображаемой плоскости. Определитель: &#83 ( ABC ).

Рис. 3.6-д Рис. 3.6-е

Необходимо отметить, что при всех случаях задания плоскость считается бесконечной.

3.4.2.Положение плоскости относительно плоскостей проекций

Плоскость относительно плоскостей проекций может занимать следующие положения:

1 – не перпендикулярно к плоскостям проекций;
2 – перпендикулярно к одной плоскости проекций;
3 – перпендикулярно к двум плоскостям проекций.

Плоскость, не перпендикулярную данным плоскостям проекций, называют плоскостью общего положения (рис.3.6).

Во втором и третьем случаях плоскости называют плоскостями частного положения.

Плоскость, перпендикулярная одной плоскости проекций.
Такие плоскости получили название проецирующих плоскостей. Горизонтально проецирующей плоскостью называют плоскость, перпендикулярную к плоскости проекций П 1 (рис.3.7).

Рис. 3.7-а Рис. 3.7-б

Любой элемент, лежащий в этой плоскости, проецируется на плоскость П 1 в прямую Г 1 , называемую горизонтальным следом плоскости. Угол наклона &#98 горизонтально проецирующей плоскости к плоскости проекций П 2 на комплексном чертеже определяется как угол &#98 1 , заключенный между горизонтальным следом Г 1 данной плоскости и прямой, перпендикулярной линиям связи (рис.3.7-б).

Рис. 3.8-а Рис. 3.8-б

Фронтально проецирующей плоскостью (рис.3.8) называют плоскость, перпендикулярную к плоскости проекций П 2 . Любой элемент этой плоскости проецируется на фронтальную плоскость проекций в прямую Ф 2 – фронтальный след плоскости. Угол наклона &#97 фронтально проецирующей плоскости к плоскости П 1 на комплексном чертеже определяется как угол &#97 2 , заключенный между фронтальным следом Ф 2 и прямой, перпендикулярной линиям связи.

Профильно проецирующей плоскостью называют плоскость, перпендикулярную к профильной плоскости проекций (рис.3.9). Любой элемент, лежащий в этой плоскости, проецируется на профильную плоскость проекций в прямую &#83 3 – профильный след плоскости. На профильной проекции углы &#97 и &#98 наклона профильно проецирующей плоскости к плоскостям П 2 и П 2 изображаются без искажения.

Рис. 3.9.

Свойство проекций геометрических элементов, лежащих в проецирующих плоскостях (см. 2.1).
Проецирующая плоскость изображается прямой линией на той плоскости проекций, к которой она перпендикулярна. Следовательно, и любая геометрическая фигура, лежащая в проецирующей плоскости, проецируется на эту плоскость в отрезок прямой.

Рис. 3.10.

Проецирующие плоскости могут быть заданы не только геометрическими элементами, лежащими в данной плоскости, но и одной линией – следом плоскости (рис.3.10). Например, горизонтально проецирующая плоскость Г может быть задана своим горизонтальным следом Г 1 . Аналогично, фронтально проецирующая плоскость может быть задана своим фронтальным следом Ф 1 .

Плоскость, перпендикулярная двум плоскостям проекций.

Плоскости, перпендикулярные двум плоскостям проекций, параллельны третьей плоскости и называются плоскостями уровня или дважды проецирующими плоскостями.
Различают три плоскости уровня: горизонтальную плоскость уровня (рис.3.11-а) – параллельную П 1 ; фронтальную плоскость уровня (рис. 3.11-6) – параллельную П 3 ; профильную плоскость уровня (рис.3.11-в) – параллельную П 3 .
Любая линия (прямая или кривая), принадлежащая плоскости уровня,будет являться линией уровня. Любая фигура, лежащая в плоскости уровня, проецируется без искажения на плоскость проекций, ей параллельную.

Рис. 3.11-а,б Рис. 3.11-в

3.4.3.Прямая и точка в плоскости

Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие плоскости,или проходит через одну точку, принадлежащую плоскости,параллельно какой-либо прямой этой плоскости. На рис. 3.12-а плоскость Г задана треугольником. Прямая 1 принадлежит плоскости Г , так как 1 принадлежит прямой 12 , а 12 принадлежит плоскости Г . Прямая m проходит через точку 3 параллельно прямой АВ , которые принадлежат плоскости Г . Следовательно, m принадлежит плоскости Г .

Рис. 3.12.

Точка принадлежит плоскости,если она расположена на прямой, принадлежащей плоскости. На рис.3.12-б показано построение фронтальной проекции точки А , принадлежащей плоскости &#83 ( m &#189&#189 n ), по заданной горизонтальной проекции. Точка А принадлежит плоскости &#83 , так как А принадлежит прямой 12 , а 12 принадлежит &#83 .

3.4.4.Главные линии плоскости

Главные линии плоскости – это особые прямые, принадлежащие плоскости, позволяющие более точно выявить ориентацию плоскости относи- тельно плоскостей проекций и упростить решение многих задач.

Главными линиями плоскости являются прямые уровня: горизонталь h , фронталь f и профильная р , а также линии наибольшего наклона, при помощи которых можно определить угол наклона плоскости к плоскостям проекций П 1 , П 2 , П 3 .

Рис. 3.13.

Линиями наибольшего наклона называют прямые данной плоскости перпендикулярные к прямым уровня этой плоскости. Прямая а наибольшего наклона плоскости Г (рис.3.1З-а) к плоскости проекций П 1 образует со своей проекцией а 1 на эту плоскость линейный угол двугранного угла плоскостей Г и П 1 . При этом плоскость &#83 ( a &#199 a 1 ) перпендикулярна прямой h пересечения этих плоскостей и, следовательно, a &#94 h и a 1 &#94 h 1 . Так как h 1 &#94 h и h 1 1 &#94 h 1 , то a &#94 h 1 и a 1 &#94 h 1 1 . Поэтому линия наибольшего наклона данной плоскости к плоскости П 1 перпендикулярна к любой горизонтали этой плоскости, и ее горизонтальная проекция перпендикулярна горизонтальной проекции любой горизонтали плоскости. Линию наибольшего наклона к П 1 часто называют линией ската.

Проведя аналогичные рассуждения относительно данной плоскости и П 2 , можно заключить, что линия наибольшего наклона плоскости к П 2 перпендикулярна к любой фронтали данной плоскости.

На рис.3.13-6 проведены: через точку С – горизонталь; через А – фронталь; через В – линия наибольшего наклона к П 1 ( &#94 h ) и линия наибольшего наклона к П 2 ( &#94 f ).

3.4.5.Параллельность плоскостей, параллельность прямой и плоскости

Плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На рис.3. На изображены две плоскости: &#83 ( n &#189&#189 l ) и Г ( АВС ). Эти плоскости параллельны, так как n &#189&#189 AC ( n 1 &#189&#189 A 1 C 1 ; n 2 &#189&#189 A 2 C 2 ); 12 (принадлежащая плоскости &#83 ) &#189&#189 AB ( 1 1 2 1 &#189&#189 A 1 B 1 ; ( 1 2 2 2 &#189&#189 A 2 B 2 ).

Рис. 3.14.

Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей плоскости. Через данную точку можно провести множество прямых, параллельных плоскости. На рис.3.14-6 одна из таких прямых b параллельна плоскости Г ( m &#189&#189 n ), так как она параллельна прямой 1 , принадлежащей плоскости Г ( b 1 &#189&#189 l 1 и b 1 &#189&#189 l 1 ).

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

2.6. Частные положения плоскостей в пространстве

Плоскость общего положения

Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций – произвольные, но отличные от 0° и 90°) называется плоскостью общего положения (рис. 2.16.а).

На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.

Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекции.

Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости).

1. Горизонтально-проецирующая плоскость a

π₁.

.

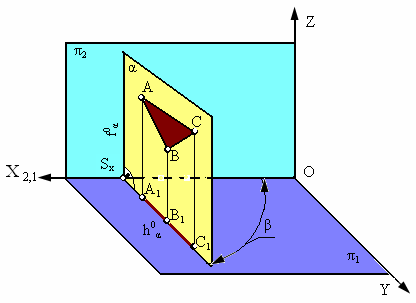
Рис. 2.13. Горизонтально-проецирующая плоскость

Плоскость α, перпендикулярная горизонтальной плоскости проекции π₁, называется горизонтально-проецирующей (рис. 2.13).

Основным свойством горизонтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π₁ в прямую линию (горизонтальный след плоскости h_a).

Угол β, который составляет горизонтальный след плоскости h_a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций π₂. Фронтальный след такой плоскости перпендикулярен оси Х (f_a

X).

2. Фронтально-проецирующая плоскость β

π₂. Плоскость b перпендикулярная фронтальной плоскости проекций π₂ называется фронтально проецирующей (рис. 2.14).

.

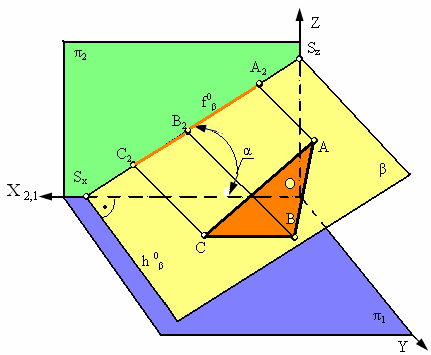
Рис. 2.14. Фронтально-проецирующая плоскость

Основным свойством фронтально-проецирующей плоскости является то, что любая фигура. Расположенная в этой плоскости, проецируется на π₂ в прямую линию (фронтальный след плоскости f_b). Угол α, который составляет фронтальный след плоскости f_b с координатной осью Х, равен углу наклона плоскости β к плоскости проекций π₁. Горизонтальный след такой плоскости перпендикулярен оси Х.

Плоскости, параллельные плоскостям проекций (плоскости уровня)

1. Горизонтальная плоскость γ

π₁.

Плоскость γ, параллельная плоскости π₁, называется горизонтальной (рис. 2.15).

.

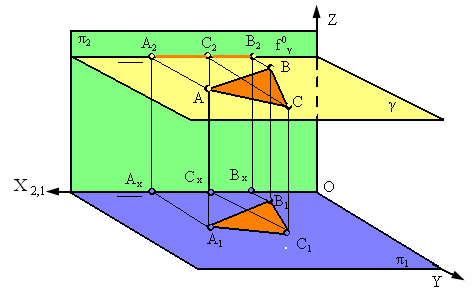
Рис. 2.15. Плоскость, параллельная горизонтальной плоскости проекций

Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (Δ А₁В₁С₁= ΔАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f_γ

Х).

2. Фронтальная плоскость δ

π₂.

Плоскость δ, параллельная плоскости π₂, называется фронтальной.

Любая фигура расположенная в такой плоскости. Проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.

Горизонтальный след фронтальной плоскости параллелен оси Х.

Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.

Плоскости и их проекции

1. Проекции плоскостей общего положения

2. Проекции плоскостей уровня

3. Проекции проецирующих плоскостей

4. Взаимное расположение двух плоскостей

5. Пересечение плоскостей общего положения

6. Взаиморасположение прямой и плоскости

Прямая – в плоскости

Прямая, параллельная плоскости

Прямая пересекает плоскость

7. Пересечение прямой с плоскостью

8. Условие видимости на чертеже

1. Проекции плоскостей общего положения

На комплексном чертеже плоскость может быть задана изображениями тех геометрических элементов, которые вполне определяют положение плоскости в пространстве. Это:

1) три точки, не лежащие на одной прямой (рис. 30);

2) прямая и точка вне прямой;

3) две параллельные прямые (рис. 27);

4) две пересекающиеся прямые (рис. 28).

При решении некоторых задач целесообразно задавать на комплексном чертеже плоскость ее следами (рис. 31).

Рис. 30 Рис. 31

СЛЕДОМ ПЛОСКОСТИ называется прямая, по которой данная плоскость пересекается с плоскостью проекций.

На рис. 31 изображена плоскость  и ее следы: с — горизонтальный; а — фронтальный; b — профильный. Следы плоскости сливаются с одноименными своими проекциями: след с = с’; след а = а”; след b = b”’. Точки

2. Проекции плоскостей уровня

Плоскостями уровня называются плоскости, параллельные плоскостям проекций.

Характерная особенность этих плоскостей состоит в том, что элементы, расположенные в этих плоскостях, проецируются на соответствующую плоскость проекций в натуральную величину.

Горизонтальная плоскость (рис. 32) параллельна горизонтальной плоскости проекций.

На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.

На рис. 32 изображена горизонтальная плоскость  (_V ).

Фронтальная плоскость (рис. 33) параллельна фронтальной плоскости проекций.

На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.

Рис. 32

Рис. 33

На рис. 33 изображена фронтальная плоскость  (_ ).

Профильная плоскость (рис. 34) параллельна профильной плоскости проекций.

На двухкартинном комплексном чертеже она изображается двумя следами: горизонтальным и фронтальным, перпендикулярными оси x.

На рис. 34 изображена профильная плоскость  (_H,V ).

3. Проекции проецирующих плоскостей

ПРОЕЦИРУЮЩИМИ называются плоскости, перпендикулярные к плоскостям проекций.

Характерной особенностью таких плоскостей является их собирательное свойство. Оно заключается в следующем: соответствующий след — проекция плоскости — собирает одноименные проекции всех элементов, расположенных в данной плоскости.

Горизонтально-проецирующая плоскость (рис. 33) перпендикулярна к горизонтальной плоскости проекций H.

Рис. 35 Рис. 36

Горизонтальные проекции всех точек, принадлежащих горизонтально-проецирующей плоскости , располагаются на горизонтальном следе — проекции _H этой плоскости (рис. 35).

Фронтально-проецирующая плоскость (рис. 36) перпендикулярна к фронтальной плоскости проекций V.

Фронтальные проекции всех точек, принадлежащих фронтально-проецирующей плоскости , располагаются на фронтальном следе — проекции _ этой плоскости (рис. 36).

Профильно-проецирующая плоскость (рис. 37) перпендикулярна к профильной плоскости проекций W.

Профильные проекции всех точек, принадлежащих профильно-проецирующей плоскости , располагаются на профильном следе —проекции этой _W плоскости (рис. 37).