Коэффициенты уравнения парной регрессии

Лекция 2. Корреляционно-регрессионный анализ. Парная регрессия

1. Сущность корреляционно-регрессионного анализа и его задачи.

2. Определение регрессии и ее виды.

3. Особенности спецификации модели. Причины существования случайной величины.

4. Методы выбора парной регрессии.

5. Метод наименьших квадратов.

6. Показатели измерения тесноты и силы связи.

7. Оценки статистической значимости.

8. Прогнозируемое значение переменной у и доверительные интервалы прогноза.

1. Сущность корреляционно-регрессионного анализа и его задачи. Экономические явления, будучи весьма разнообразными, характеризуются множеством признаков, отражающих определенные свойства этих процессов и явлений и подверженных взаимообусловленным изменениям. В одних случаях зависимость между признаками оказывается очень тесной (например, часовая выработка работника и его заработная плата), а в других случаях такая связь не выражена вовсе или крайне слаба (например, пол студентов и их успеваемость). Чем теснее связь между этими признаками, тем точнее принимаемые решения.

Различают два типа зависимостей между явлениями и их признаками:

функциональная (детерминированная, причинная) зависимость. Задается в виде формулы, которая каждому значению одной переменной ставит в соответствие строго определенное значение другой переменной (воздействием случайных факторов при этом пренебрегают). Иными словами, функциональная зависимость – это связь, при которой каждому значению независимой переменной х соответствует точно определенное значение зависимой переменной у. В экономике функциональные связи между переменными являются исключениями из общего правила;

статистическая (стохастическая, недетерминированная) зависимость – это связь переменных, на которую накладывается воздействие случайных факторов, т.е. это связь, при которой каждому значению независимой переменной х соответствует множество значений зависимой переменной у, причем заранее неизвестно, какое именно значение примет у.

Частным случаем статистической зависимости является корреляционная зависимость.

Корреляционная зависимость – это связь, при которой каждому значению независимой переменной х соответствует определенное математическое ожидание (среднее значение) зависимой переменной у.

Корреляционная зависимость является «неполной» зависимостью, которая проявляется не в каждом отдельном случае, а только в средних величинах при достаточно большом числе случаев. Например, известно, что повышение квалификации работника ведет к росту производительности труда. Это утверждение часто подтверждается на практике, но не означает, что у двух и более работников одного разряда / уровня, занятых аналогичным процессом, будет одинаковая производительность труда.

Корреляционная зависимость исследуется с помощью методы корреляционного и регрессионного анализа.

Корреляционно-регрессионный анализ позволяет установить тесноту, направление связи и форму этой связи между переменными, т.е. ее аналитическое выражение.

Основная задача корреляционного анализа состоит в количественном определении тесноты связи между двумя признаками при парной связи и между результативными и несколькими факторными признаками при многофакторной связи и статистической оценке надежности установленной связи.

2. Определение регрессии и ее виды. Регрессионный анализ является основным математико-статистическим инструментом в эконометрике. Регрессией принято называть зависимость среднего значения какой-либо величины (y) от некоторой другой величины или от нескольких величин (x_i).

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая (парная) регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция одной независимой (объясняющей) переменной х. В неявном виде парная регрессия – это модель вида:

.

,

где a и b – оценки коэффициентов регрессии.

Множественная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция нескольких независимых (объясняющих) переменных х₁, х₂, … х_n. В неявном виде парная регрессия – это модель вида:

.

,

где a и b₁, b₂, b_n – оценки коэффициентов регрессии.

Примером такой модели может служить зависимость заработной платы работника от его возраста, образования, квалификации, стажа, отрасли и т.д.

Относительно формы зависимости различают:

нелинейную регрессию, предполагающую существование нелинейных соотношений между факторами, выражающихся соответствующей нелинейной функцией. Зачастую нелинейные по внешнему виду модели могут быть приведены к линейному виду, что позволяет их относить к классу линейных.

3. Особенности спецификации модели. Причины существования случайной величины. Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными.

Прежде всего из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. В уравнении регрессии корреляционная связь представляется в виде функциональной зависимости, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых:

,

где у – фактическое значение результативного признака;

– теоретическое значении результативного признака, найденное исходя из уравнения регрессии;

– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина

называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Присутствие в модели случайной величины порождено тремя источниками:

выборочным характером исходных данных,

особенностями измерения переменных.

К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции, но и недоучет в уравнении регрессии какого-либо существенного фактора (использование парной регрессии вместо множественной).

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерностей связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. Исходных данных

Однако наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.

4. Методы выбора парной регрессии. Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях отводится ошибкам спецификации модели. В парной регрессии выбор вида математической функции

может быть осуществлен тремя методами:

аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемых при количественной оценке связей

Класс математических функций для описания связи двух переменных достаточно широк, также используются и другие типы кривых.

Аналитический метод выбор типа уравнения регрессии основан на изучении материальной природы связи исследуемых признаков, а также визуальной оценке характера связи. Т.е. если мы говорим о кривой Лаффера, показывающей зависимость между прогрессивностью налогообложения и доходами бюджета, то речь идет о параболической кривой, а в микроанализе изокванты представляют собой гиперболы.

Уравнения линейной регрессии (стр. 1 из 3)

Министерство образования и науки РФ

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Филиал в г. Туле

по дисциплине «Эконометрика»

По предприятиям легкой промышленности получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х, млн. руб.) табл. 1.

Х	33	17	23	17	36	25	39	20	13	12
Y	43	27	32	29	45	35	47	32	22	24

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора Х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения Y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

1. Линейная модель имеет вид:

Параметры уравнения линейной регрессии найдем по формулам

Расчет значения параметров представлен в табл. 2.

1 43 33 1419 1089 42,236 0,764 0,584 90,25 88,36 0,018 2 27 17 459 289 27,692 -0,692 0,479 42,25 43,56 0,026 3 32 23 736 529 33,146 -1,146 1,313 0,25 2,56 0,036 4 29 17 493 289 27,692 1,308 1,711 42,25 21,16 0,045 5 45 36 1620 1296 44,963 0,037 0,001 156,25 129,96 0,001 6 35 25 875 625 34,964 0,036 0,001 2,25 1,96 0,001 7 47 39 1833 1521 47,69 -0,69 0,476 240,25 179,56 0,015 8 32 20 640 400 30,419 1,581 2,500 12,25 2,56 0,049 9 22 13 286 169 24,056 -2,056 4,227 110,25 134,56 0,093 10 24 12 288 144 23,147 0,853 0,728 132,25 92,16 0,036 ∑ 336 235 8649 6351 12,020 828,5 696,4 0,32 Средн. 33,6 23,5 864,9 635,1

Определим параметры линейной модели

Линейная модель имеет вид

2. Вычислим остатки

Расчеты представлены в табл. 2.

Рис. 1. График остатков ε.

3. Проверим выполнение предпосылок МНК на основе критерия Дарбина-Уотсона.

0,584 2,120 0,479 0,206 1,313 6,022 1,711 1,615 0,001 0,000 0,001 0,527 0,476 5,157 2,500 13,228 4,227 2,462 0,728 31,337 12,020

d1=0,88; d2=1,32 для α=0,05, n=10, k=1.

значит, ряд остатков не коррелирован.

4. Осуществим проверку значимости параметров уравнения на основе t-критерия Стьюдента. (α=0,05).

5. Найдем коэффициент корреляции по формуле

Расчеты произведем в табл. 2.

Коэффициент детерминации найдем по формуле

Проверим значимость уравнения регрессии с помощью F-критерия Фишера

Fтаб=5,32, т.к. k1=1, k2=8, α=0,05

т.к. F значительно больше Fтабл, то можно сделать вывод, что уравнение регрессии с вероятностью 95% статистически значимо.

Оценим точность модели на основе использования средней относительной ошибки аппроксимации.

Расчеты произведены в табл. 2.

значит, линейную модель можно считать точной, т.к. Е

Коэффициенты уравнения парной линейной регрессии

Министерство науки и образования РК

Евразийский Технологический Университет

РЕФЕРАТ

На тему: «Регрессионный анализ»

Выполнила: Самазбаева А.

Проверила: Иматаева А.

Оглавление

1. Корреляционные поля и цель их построения

2. Понятие регрессии

2.1 Уравнение линейной регрессии

2.2 Коэффициенты уравнения парной линейной регрессии

2.3 Связь между коэффициентами регрессии и корреляции

2.4 Определение параметров парной линейной регрессии

2.5 Графическое представление уравнения парной линейной Регрессии

Введение

Обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимает корреляционный и регрессионный анализы обработки статистических данных.

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и регрессионного анализа. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей.

Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

Корреляционные поля и цель их построения

Корреляция изучается на основании экспериментальных данных, представляющих собой измеренные значения (xi, yi) двух признаков. Если экспериментальных данных немного, то двумерное эмпирическое распределение представляется в виде двойного ряда значений xi и yi. При этом корреляционную зависимость между признаками можно описывать разными способами. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.

Корреляционный анализ, как и другие статистические методы, основан на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из которой получены экспериментальные значения xi и yi.

Когда исследуется корреляция между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (метры, секунды, килограммы и т.д.), то очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель отображает зависимость между переменными величинами xi и yi графически в виде геометрического места точек в системе прямоугольных координат. Эту графическую зависимость называются также диаграммой рассеивания или корреляционным полем.

Данная модель двумерного нормального распределения (корреляционное поле) позволяет дать наглядную графическую интерпретацию коэффициента корреляции, т.к. распределение в совокупности зависит от пяти параметров: mx, my – средние значения (математические ожидания); sx,sy – стандартные отклонения случайных величин Х и Y и р – коэффициент корреляции, который является мерой связи между случайными величинами Х и Y.

Если р = 0, то значения, xi, yi, полученные из двумерной нормальной совокупности, располагаются на графике в координатах х, у в пределах области, ограниченной окружностью (рис.1.3, а). В этом случае между случайными величинами Х и Y отсутствует корреляция и они называются некоррелированными. Для двумерного нормального распределения некоррелированность означает одновременно и независимость случайных величин Х и Y.

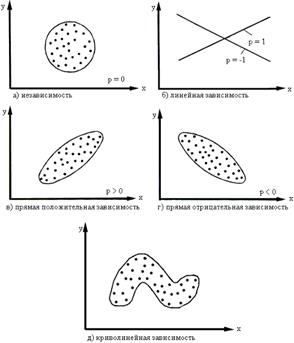
Рис.1.3. Графическая интерпретация взаимосвязи между показателями.

Если р = 1 или р = -1, то между случайными величинами Х и Y существует линейная функциональная зависимость (Y = c + dX). В этом случае говорят о полной корреляции. При р = 1 значения xi, yi определяют точки, лежащие на прямой линии, имеющей положительный наклон (с увеличением xi значения yi также увеличиваются), при р = -1 прямая имеет отрицательный наклон (рис.1.3, б).

В промежуточных случаях (-1 0 имеет место положительная корреляция (с увеличением xi значения yi имеют тенденцию к возрастанию), при p

Дата добавления: 2019-02-12 ; просмотров: 24 ; ЗАКАЗАТЬ РАБОТУ

Линейная парная регрессия (стр. 1 из 4)

1. Линейная парная регрессия

Корреляционная зависимость может быть представлена в виде

В регрессионном анализе рассматривается односторонняя зависимость случайной переменной Y от одной (или нескольких) неслучайной независимой переменной Х . Такая зависимость Y от X (иногда ее называют регрессионной ) может быть также представлена в виде модельного уравнения регрессии Y от X (1). При этом зависимую переменную Y называют также функцией отклика (объясняемой, выходной, результирующей, эндогенной переменной, результативным признаком), а независимую переменную Х – объясняющей (входной, предсказывающей, предикторной, экзогенной переменной, фактором, регрессором, факторным признаком).

Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная Х примет значение х , т.е. Х = х . В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (x_i , y_i ) ограниченного объема n . В этом случае речь может идти об оценке (приближенном выражении, аппроксимации) по выборке функции регрессии. Такой оценкой является выборочная линия (кривая) регрессии :

Уравнение (2) называется выборочным уравнением регрессии .

В дальнейшем рассмотрим линейную модель и представим ее в виде

Для решения поставленной задачи определим формулы расчета неизвестных параметров уравнения линейной регрессии (b , b ₁ ).

Согласно методу наименьших квадратов (МНК) неизвестные параметры b и b ₁ выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значенийy_i от значений

На основании необходимого условия экстремума функции двух переменных S = S (b , b ₁ ) (4) приравняем к нулю ее частные производные, т.е.

откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:

Теперь, разделив обе части уравнений (5) на n , получим систему нормальных уравнений в следующем виде:

где соответствующие средние определяются по формулам:

Решая систему (6), найдем

Коэффициент b ₁ называется выборочным коэффициентом регрессии Y по X .

Коэффициент регрессии Y по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.

Отметим, что из уравнения регрессии

На первый взгляд, подходящим измерителем тесноты связи Y от Х является коэффициент регрессии b ₁ . Однако b ₁ зависит от единиц измерения переменных. Очевидно, что для “исправления” b ₁ как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Если представить уравнение

В этой системе величина

Если r > 0 (b ₁ > 0), то корреляционная связь между переменными называется прямой, если r 2 . (20)

4. Возмущения e_i и e_j не коррелированны:

5. Возмущения e_i есть нормально распределенная случайная величина.

Оценкой модели (18) по выборке является уравнение регрессии

Теорема Гаусса – Маркова . Если регрессионная модель
y_i = b + b₁x_i + e_i удовлетворяет предпосылкам 1-5, то оценкиb , b ₁ имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Таким образом, оценки b и b ₁ в определенном смысле являются наиболее эффективными линейными оценками параметров b и b₁ .

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Для проверки значимости выдвигают нулевую гипотезу о надежности параметров. Вспомним основные понятия и определения необходимые для анализа значимости параметров регрессии.

Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным.

Парная регрессия. – Шпаргалки к экзамену – Эконометрия

Парной регрессией называется уравнение связи двух переменных

где у – зависимая переменная (результативный признак);

х – независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Метод наименьших квадратов МНК

Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.

5. Оценка статистической значимости показателей корреляции, параметров уравнения парной линейной регрессии, уравнения регрессии в целом.

6. Оценка степени тесноты связи между количественными переменными. Коэффициент ковариации. Показатели корреляции: линейный коэффициент корреляции, индекс корреляции (= теоретическое корреляционное отношение).

Мч(у) – Т.е. получим корреляционную зависимость.

Наличие корреляционной зависимости не может ответить на вопрос о причине связи. Корреляция устанавливает лишь меру этой связи, т.е. меру согласованного варьирования.

Меру взаимосвязи му 2 мя переменными можно найти с помощью ковариации.

, ,

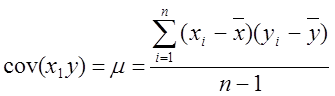
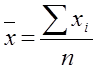
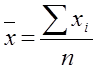
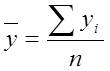
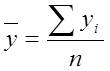
Величина показателя ковариации зависит от единиц в γ измеряется переменная. Поэтому для оценки степени согласованного варьирования используют коэффициент корреляции – безразмерную характеристику имеющую определенный пределы варьирования..

7. Коэффициент детерминации. Стандартная ошибка уравнения регрессии.

Коэффициент детерминации (rxy2) – характеризует долю дисперсии результативного признака y, объясняемую дисперсией, в общей дисперсии результативного признака. Чем ближе rxy2 к 1, тем качественнее регрессионная модель, то есть исходная модель хорошо аппроксимирует исходные данные.

8. Оценка стат значимости показателей корр-ии, параметров уравнения парной линейной регрессии, уравнения регрессии в целом: t-критерий Стьюдента, F-критерий Фишера.

9. Нелинейные модели регрессии и их линеаризация.

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно исключенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам:

Нелинейные модели регрессии и их линеаризация

При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются по МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию

,

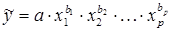
мы преобразовываем ее в линейный вид:

,

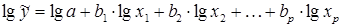
где переменные выражены в логарифмах.

Далее обработка МНК та же: строится система нормальных уравнений и определяются неизвестные параметры. Потенцируя значение

, находим параметр a и соответственно общий вид уравнения степенной функции.

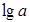
Вообще говоря, нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Эта оценка определяется, как и в линейной регрессии, МНК. Так, в двухфакторном уравнении нелинейной регрессии

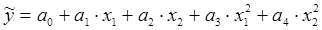
может быть проведена линеаризация, введением в него новых переменных

. В результате получается четырехфактороное уравнение линейной регрессии

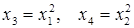
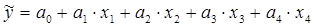
10.Мультиколлинеарность. Методы устранения мультиколлинеарности.

Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности.

Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).

Включение в модель мультиколлинеарных факторов нежелательно по следующим причинам:

ü затрудняется интерпретация параметров множественной регрессии; параметры линейной регрессии теряют экономический смысл;

ü оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений, что делает модель непригодной для анализа и прогнозирования

Методы устранения мультиколлинеарности

– исключение переменной (ых) из модели;

Однако нужна определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации.

– получение дополнительных данных или построение новой выборки;

Иногда для уменьшения мультиколлинеарности достаточно величить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным. Увеличение количества данных уменьшает дисперсии коэффициентов регрессии и тем самым увеличивает их статистическую значимость. Однако получение новой выборки или расширение старой не всегда возможно или связано с серъезными издержками. Кроме того, такой подход может увеличить

– изменение спецификации модели;

В ряде случаев проблема мультиколлинеарности может быть решена путем изменения спецификации модели: либо меняется форма модели, либо добавляются новые объясняющие переменные, не учтенные в модели.

– использование предварительной информации о некоторых параметрах;

11.Классическая линейная модель множественной регр-ии (КЛММР). Определение параметров ур-я множественной регр-ии методом наим квадратов.

Парная регрессия

Взаимосвязанные признаки подразделяются на факторные (под их воздействием изменяются другие, зависящие от них признаки) и результативные (изменяющихся под воздействием факторных признаков).

Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, при большом количестве наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

Прямолинейная зависимость в этом случае может быть выражена уравнением прямой:

Параметр a₁ называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака y при отклонении величины факторного признака x на одну единицу.

Параметр a показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов.

Алгоритм выполнения индивидуального задания 2

Парная регрессия характеризует связь между двумя признаками: результативным (y) факторным (x). Аналитически линейная связь между ними описывается уравнением прямой ;

Скопируйте файл «Численность населения» на лист Excel.

Скопируйте данные своего варианта задания 1 (без регионов) в следующий столбец.

Исключите суммарные итоги по федеральным округам и Российской федерации в целом (удалите эти строки).

Вычислите средние значения по обоим факторам.

Организуйте столбцы Yi-Yсред, (Yi-Yсред) 2 , Xi-Xсред, (Xi-Xсред) 2 , (Yi-Yсред)*(Xi-Xсред). Произведите расчеты этих столбцов.

Рассчитайте суммарные значения столбцов

Рассчитайте коэффициент регрессии а₁.

В уравнениях регрессии параметр параметр а₁ — коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.

Коэффициент регрессии а₁ рассчитается коэффициент регрессии а₁ по формуле:

Коэффициент регрессии означает, что при увеличении а₁ – оборота розничной торговли на единицу (один миллиард рублей) численность населения увеличится на 0,05 человека, т.е чтобы численность населения увеличилась на 1 человека, оборот розничной торговли должен увеличится в 20 раз.

Рассчитайте свободный член уравнения регрессии а_.В уравнениях регрессии параметр а показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов.

Свободный член а в уравнении регрессии означает, что если оборота розничной торговли не будет вовсе, численность населения составит 1258,18 человек. Если бы свободный член был отрицательным, то это бы означало, что х не может быть равен нулю или близким к нулю.

Рассчитайте тесноту связи между рассматриваемыми факторами по величине коэффициента корреляции.

Величина коэффициента корреляции

Характер тесноты связи

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются в противоположном направлении по сравнению с изменением факторного признака.

Коэффициент корреляции рассчитывается по формуле

Коэффициент корреляции показывает, что связь между факторами сильная.

Рассчитайте коэффициент детерминации по формуле r_yx2 =0,8 2 =0,64, который характеризует долю вариации результативного признака Y под воздействием всех изучаемых факторных признаков, то есть долю дисперсии отклонений зависимой переменной от её среднего значения, объясняемую рассматриваемой моделью связи.

Проведите статистическую оценку надежности (значимости) параметров парной регрессии

Для коэффициента парной регрессии а₁ средняя ошибка оценки

где – расчётные значения результативного признака для i-й единицы;

n- 2 — число степеней свободы (теряются 2 степени свободы, поскольку линейная парная регрессия имеет два параметра).

Рассчитывается столбец с расчётными значениями по уравнению регрессии y=а+а₁х=1258,18+0,05x.

находится отношение коэффициента к его средней ошибке, т.е. t-критерий Стьюдента:

Табличное значение t-критерия Стьюдента при 16 – 2 степенях свободы и уровне значимости 0,05 составляет 2,14 (функция СТЬЮДРАСПОБР).

Полученное значение критерия намного больше, следовательно, вероятность нулевого значения коэффициента регрессии менее 0,05, то есть Коэффициент регрессии значим.

32. Произведите статистическую оценку надежности (значимости) коэффициента корреляции.

Для проверки существенности связи между группировочным признаком и вариацией исследуемого признака используется F-критерий Фишера.

В нашем примере Fкр=3,96 (функция FРАСПРОБР) при уровне значимости 0,05, степенях свободы v₁ = m-1; v₂ = N-m;

где m – число факторов (при парной корреляции равно 2,

N – число наблюдений,

Поскольку Fрасч >Fкp, коэффициент корреляции значим, наличие связи доказано, т.е. это говорит о наличии связи между факторным и результативным признаками.