График проекции перемещения тела

График проекции перемещения тела

Главная цель Проверялкина – тренировка умения работать с параграфом: находить/выделять нужные по смыслу фрагменты, выбирать из нескольких подходящих фрагментов более удачный, многократно обращаться к тексту для поиска очередного ответа. В результате ваша зрительная память «схватывает» расположение в тексте важных моментов: определений, закономерностей, выводов; вы привыкаете к терминам и формулировкам. Другими словами, неоднократно перечитывая текст при поиске наилучшего ответа, вы полнее и обдуманнее воспринимаете физику.

Как и любой человек, Проверялкин «хочет» видеть не любой правильный ответ, а тот, который он считает наилучшим. Не расстраивайтесь, просто поищите другой ответ. Ведь разве плохо то, что вы будете знать несколько правильных ответов на один вопрос. Мы рекомендуем обсуждать задания с одноклассниками через наушники с микрофоном (или по телефону).

Важно: для Проверялкина правильным ответом является не только содержательно правильный, но и правильно «добытый». То есть ответы на задания Проверялкина нужно «перетаскивать» из параграфа, а не печатать «от себя» или копировать из других источников, например «готовых домашних заданий». Давайте вспомним, какова главная цель вашей беседы с Проверялкиным? Правильно – тренировка умения работать с материалом параграфа учебника!

Для перехода к проверялкам по темам кликайте номера тем вверху: 01 02 03 04 05 и т.д.

Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей

Прямолинейное равномерное движение

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела

за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: Проекция перемещения на ось ОХ равна: где x – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид: Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

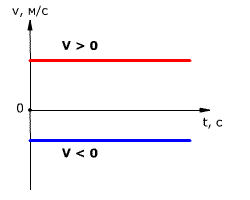
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

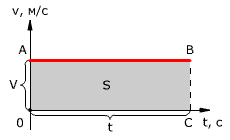
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна где α – угол наклона графика к оси времени.

Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

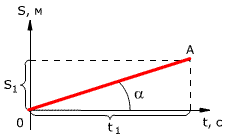
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂). Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

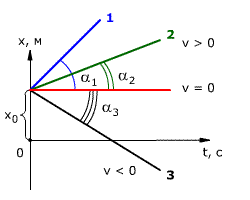
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

График проекции перемещения.

Проекция перемещения при равномерном прямолинейном движении определяется формулой:

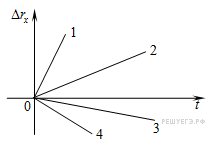
График проекции перемещения при равномерном прямолинейном движении — это прямая, выходящая из начала координат.

Направление движения: если прямая лежит над осью времени (поднимается вверх), то тело движется в положительном направлении оси Ox (прямые 1 и 2); если прямая лежит под осью времени (опускается вниз), то тело движется против оси Ox.

Значение скорости: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль скорости

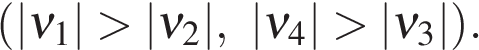
Закон движения.

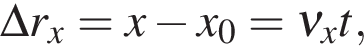
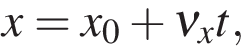
где

— начальная координата тела по оси Ox, x — координата тела в момент времени t, — проекция скорости на ось Ox.

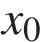
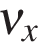
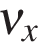
При движении по прямой всегда возможно выбрать ось Ox вдоль этой прямой. Однако в некоторых случаях удобно рассматривать движение и вдоль оси Oy:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8322 –

| 7260 – или читать все.

185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Перемещении при прямолинейном равноускоренном движении

1. Нахождение пути по графику зависимости скорости от времени

Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.

Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.

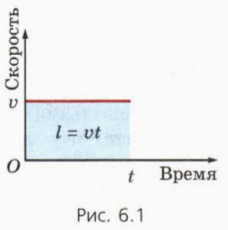
Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении

путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.

Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.

Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.

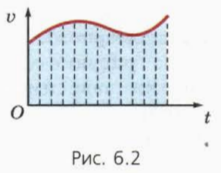
Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).

Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)

2. Путь и перемещение при прямолинейном равноускоренном движении

Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.

Начальная скорость тела равна нулю

Направим ось x в сторону ускорения тела. Тогда a_x = a, v_x = v. Следовательно,

На рисунке 6.3 изображен график зависимости v(t).

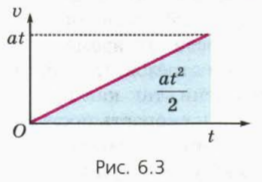
? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.

Этим равноускоренное движение существенно отличается от равномерного.

На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.

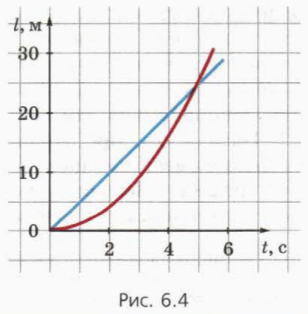
? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?

? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?

Найдем теперь зависимость проекции перемещения s_x от времени. В данном случае проекция ускорения на ось x положительна, поэтому s_x = l, a_x = a. Таким образом, из формулы (2) следует:

Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда s_x

Начальная скорость тела не равна нулю

Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой

где v_0x – проекция начальной скорости на ось x.

Мы рассмотрим далее случай, когда v_0x > 0, a_x > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).

На рисунке 6.6 изображен график зависимости v_x(t) при v_0x > 0, a_x > 0.

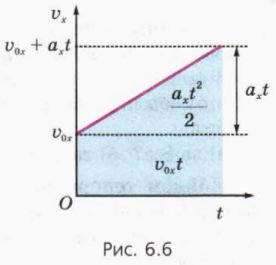
? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения

Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения s_x соотношением

где x — начальная координата тела. Следовательно,

Из формул (5), (6) получаем:

6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t 2 .
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.

3. Соотношение между путем и скоростью

При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:

Подставим это выражение в формулу (2) для пути:

l = at 2 /2 = a/2(v/a) 2 = v 2 /2a. (9)

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.

? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?

Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).

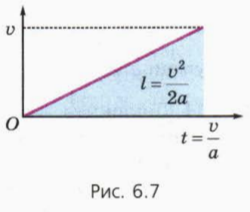
Это соображение поможет вам легко справиться со следующим заданием.

? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь l_т = v 2 /2a, где v – начальная скорость тела, a – модуль ускорения.

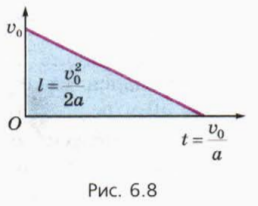
В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v и путь, пройденный при разгоне с места до скорости v с тем же по модулю ускорением a, одинаковы.

? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с 2 . Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с 2 . Сравните найденные вами значения тормозного пути с длиной классной комнаты.

? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v 2 – v 2 )/2a, если скорость тела увеличивается;
б) l = (v 2 – v 2 )/2a, если скорость тела уменьшается.

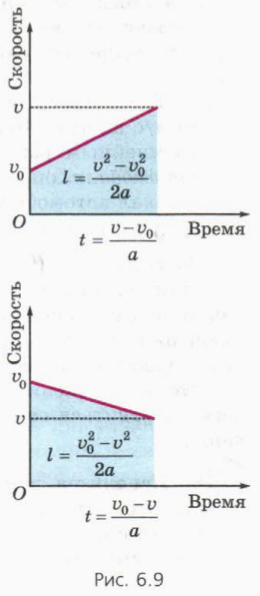
? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением

? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?

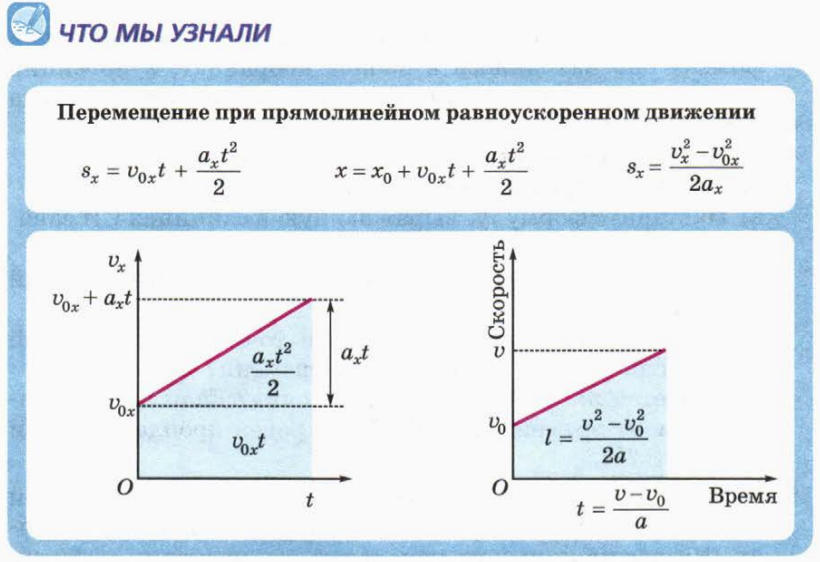
Дополнительные вопросы и задания

13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?

14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?

15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости v_x(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?

16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t₁ и t₂ после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t₁ и t₂ составьте систему двух уравнений с двумя неизвестными v и a.
в) Решив эту систему уравнений, выразите v и a через b, t₁ и t₂.
г) Выразите весь пройденный шариком путь l через b, t₁ и t₂.
д) Найдите числовые значения v, a и l при b = 30 см, t₁ = 1с, t₂ = 2 с.
е) Постройте графики зависимости v_x(t), s_x(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.

Геометрический смысл перемещения

При равномерном прямолинейном движении перемещение определяют по формуле

. Такой же результат получим, если вычислим площадь фигуры под графиком скорости в осях . Значит, для определения пути и модуля перемещения при прямолинейном движении необходимо вычислять площадь фигуры под графиком скорости в осях :

График проекции перемещения — зависимость проекции перемещения от времени.

График проекции перемещения при равномерном прямолинейном движении — прямая, выходящая из начала координат (1, 2, 3).

Если прямая (1) лежит над осью времени, то тело движется по направлению оси ОХ, а если под осью (2, 3), то против оси ОХ.

Чем больше тангенс утла наклона (1) графика, тем больше модуль скорости.

График координаты — зависимость координаты тела от времени:

График координаты при равномерном прямолинейном движении — прямые (1, 2, 3).

Если с течением времени координата увеличивается (1, 2), то тело движется по направлению оси ОХ; если координата уменьшается (3), то тело движется против направления оси ОХ.

Чем больше тангенс угла наклона (1), тем больше модуль скорости.

Если графики координат двух тел пересекаются, то из точки пересечения следует опустить перпендикуляры на ось времени и ось координат.

физический словарик (кинематика)

Скорость (v) – физическая величина, численно равна пути (s), пройденного телом за единицу времени (t).

Путь (S) – длина траектории, по которой двигалось тело, численно равен произведению скорости (v) тела на время (t) движения.

Время движения

Время движения (t) равно отношению пути (S), пройденного телом, к скорости (v) движения.

Средняя скорость

Средняя скорость (vср) равна отношению суммы участков пути (s₁ s₂, s₃, . ), пройденного телом, к промежутку времени (t₁+ t₂+ t₃+ . ), за который этот путь пройден.

Средняя скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Средняя скорость при неравномерном движении по прямой:

это отношение всего пути ко всему времени.

Два последовательных этапа с разными скоростями:

где

При решении задач – сколько этапов движения столько будет составляющих:

Проекции вектора перемещения на оси координат

Проекция вектора перемещения на ось ОХ:

Проекция вектора перемещения на ось OY:

Проекция вектора на ось равна нулю, если вектор перпендикулярен оси.

Знаки проекций перемещения: проекцию считают положительной, если движение от проекции начала вектора к проекции конца происходит по направлению оси, и отрицательной, если против оси. В данном примере

Модуль перемещения – это длина вектора перемещения:

По теореме Пифагора:

Проекции перемещения и угол наклона

В данном примере:

Уравнение координаты (в общем виде):

Радиус-вектор — вектор, начало которого совпадает с началом координат, а конец — с положением тела в данный момент времени. Проекции радиус-вектора на оси координат определяют координаты тела в данный момент времени.

Радиус-вектор позволяет задать положение материальной точки в заданной системе отсчета:

Равномерное прямолинейное движение – определение

Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени, совершает равные перемещения.

Скорость при равномерном прямолинейном движении. Скорость

— векторная физическая величина, которая показывает, какое перемещение совершает тело за единицу времени.

В векторном виде:

В проекциях на ось ОХ:

Дополнительные единицы измерения скорости:

1 км/ч = 1000 м/3600 с,

Измерительный прибор — спидометр — показывает модуль скорости.

Знак проекции скорости зависит от направления вектора скорости и оси координат:

График проекции скорости представляет собой зависиость проекции скорости от времени:

График скорости при равномерном прямолинейном движении — прямая, параллельная оси времени (1, 2, 3).

Если график лежит над осью времени (.1), то тело движется по направлению оси ОХ. Если график расположен под осью времени, то тело движется против оси ОХ (2, 3).

Чем дальше график от оси времени, тем больше модуль скорости (3).

Геометрический смысл перемещения.

При равномерном прямолинейном движении перемещение определяют по формуле

. Такой же результат получим, если вычислим площадь фигуры под графиком скорости в осях . Значит, для определения пути и модуля перемещения при прямолинейном движении необходимо вычислять площадь фигуры под графиком скорости в осях :

График проекции перемещения — зависимость проекции перемещения от времени.

График проекции перемещения при равномерном прямолинейном движении — прямая, выходящая из начала координат (1, 2, 3).

Если прямая (1) лежит над осью времени, то тело движется по направлению оси ОХ, а если под осью (2, 3), то против оси ОХ.

Чем больше тангенс утла наклона (1) графика, тем больше модуль скорости.

График координаты — зависимость координаты тела от времени:

График координаты при равномерном прямолинейном движении — прямые (1, 2, 3).

Если с течением времени координата увеличивается (1, 2), то тело движется по направлению оси ОХ; если координата уменьшается (3), то тело движется против направления оси ОХ.

Чем больше тангенс угла наклона (1), тем больше модуль скорости.

Если графики координат двух тел пересекаются, то из точки пересечения следует опустить перпендикуляры на ось времени и ось координат.

Относительность механического движения

Под относительностью мы понимаем зависимость чего-либо от выбора системы отсчета. Например, покой относителен; движение относительно и положение тела относительно.

Правило сложения перемещений. Векторная сумма перемещений

где

— перемещение тела относительно подвижной системы отсчета (ПСО); — перемещение ПСО относительно неподвижной системы отсчета (НСО); — перемещение тела относительно неподвижной системы отсчета (НСО).

Векторное сложение:

Сложение векторов, направленных вдоль одной прямой:

Сложение векторов, перпендикулярных друг другу

По теореме Пифагора

Сложение векторов, расположенных под углом друг к другу

Правило сложения скоростей. Векторная сумма скоростей:

где

— скорость тела относительно подвижной системы отсчета (ПСО); — скорость ПСО относительно неподвижной системы отсчета (НСО); — скорость тела относительно неподвижной системы отсчета (НСО).

Относительная скорость. Векторная разность скоростей:

где

— скорость первого тела относительно второго (относительная скорость); — скорость первого тела; — скорость второго тела.

Вычитание векторов, направленных по одной прямой:

Вычитание векторов перпендикулярных друг другу

Вычитание векторов, расположенных под углом друг к другу:

ИЗД Механика поступательного и вращательного движения. 26.1. На рисунке изображен график зависимости проекции Sx перемещения тела на ось ОХ, вдоль которой тело движется

Вариант 26

26.1. На рисунке изображен график зависимости проекции S_x перемещения тела на ось ОХ, вдоль которой тело движется, от времени t. График представляет собой параболу. Найдите проекцию V_x начальной скорости тела.

26.2. Санки массой m = 10 кг, стоящие на льду, в течение t =1,0 с тянут с постоянной силой F = 100 Н при помощи веревки, образующей угол α = 45 0 с горизонтом, после чего веревку отпускают и забрасывают на санки. Коэффициент трения санок о лед μ = 0,10. Пренебрегая массой веревки, определить путь l_Σ , пройденный санками за все время их движения.

26.3. Тело брошено под углом α = 30 0 к горизонту. За время Δt = 5 с полета модуль изменения импульса тела равен Δр = 200

.Сопротивление воздуха не учитывать. Масса этого тела равна … кг.

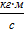
26.4. Сваю массой m = 100 кг забивают в грунт копром массой М = 400 кг. Копер свободно падает с высоты Н = 5 м, и при каждом его ударе свая опускается на глубину h = 25 см. Определить силу сопротивления грунта, считая ее постоянной, и КПД неупругого удара копра о сваю.

26.5. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол ( в рад) окажется тело повернутым относительно начального положения через 10 с после начала движения.

26.6 Блок, массу m = 2,0 кг которого можно считать равномерно распределенной по ободу, вращается с начальной частотой n = 12 об/с. Диаметр блока равен D = 30 см. Определите, какой момент сил надо приложить к блоку, чтобы он, двигаясь равнозамедленно, остановился в течение Δ t = 8,0 с. Сколько оборотов он сделает до остановки?

26.7

. На графике приведена зависимость проекции момента силы, действующей на тело, от времени. Какой момент импульса будет иметь тело к концу третьей секунды движения, если в начальный момент t = 0 тело покоилось?

26.8. Шар массой m = 3 кг скатывается без проскальзывания с вершины наклонной плоскости высотой h=4 м без начальной скорости. Длина ската наклонной плоскости l = 8 м, а значение коэффициента трения одинаково на протяжении всего пути и равно m =0,1. Найдите расстояние, которое пройдет шар от подножья наклонной плоскости до своей полной остановки.

xn----ctbetbqubfsc3c1hk.xn--p1ai – Студопедия.Орг – 2014-2019 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.001 с) .

§ 4. Перемещение при прямолинейном равномерном движении. –

ВОПРОСЫ

1. Что называется скоростью прямолинейного равномерного движения?

2. Как найти проекцию вектора перемещения тела, движущегося прямолинейно и равномерно, если известна проекция вектора скорости движения?

По формуле: S_x= v_xt, где S_x – проекция вектора перемещения на ось Х, v_x – проекция вектора скорости движения, t – время перемещения.

3. При каком условии модуль вектора перемещения, совершенного телом за некоторый промежуток времени, равен пути, пройденному телом за тот же промежуток времени?

4. Докажите, что при равномерном движении модуль вектора перемещения численно равен площади под графиком скорости.

5. Какую информацию о движении двух тел можно получить по графикам, изображенным на рисунке 7?

Первое тело движется сонаправленно с осью Х с модулем скорости v = 30 км/ч, а второе тело движется в противоположном направлении с модулем скорости v = 25 км/ч.

1. Может ли находиться под осью О_t (т.е. в области отрицательных значений оси скорости) график модуля вектора скорости? график проекции вектора скорости?

Модуль вектора скорости всегда положителен, поэтому его график не может быть под осью О_t , а проекция вектора скорости может быть и отрицательной.

2. Постройте графики зависимости проекций векторов скорости от времени для трёх автомобилей, движущихся прямолинейно и равномерно, если два из них едут в одном направлении, а третий – навстречу им. Скорость первого автомобиля равна 60 км/ч, второго – 80 км/ч, а третьего – 90 км/ч.