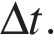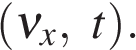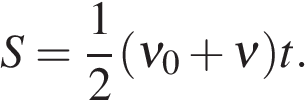Татьяна Ефимова предлагает статью на тему: "проекция скорости земли" с детальным описанием.
Содержание
- 1 1. МЕХАНИКА 1.1. Кинематика
- 2 Проекция скорости земли
- 3 График проекции скорости в зависимости от времени.
- 4 Вектор мгновенной скорости. Проекции вектора скорости. Модуль вектора скорости.
- 5 Проекция скорости земли
- 6 Проекция скорости земли
- 7 Движение тела, брошенного под углом к горизонту (бросок)
- 8 Способ измерения проекций горизонтальной составляющей вектора угловой скорости вращения земли для определения азимутального направления (компасирования)
1. МЕХАНИКА
1.1. Кинематика
Движение с ускорением
Равноускоренное прямолинейное движение – движение по прямой с постоянным ускорением (а = const ).
Ускорение а (размерность: м/с 2 ) – векторная физическая величина, показывающая, на сколько изменяется скорость тела за 1 с.
В векторном виде:
В проекции на ось ОХ формула аналогичная
Знаки проекции ускорения зависят от направления вектора ускорения и оси – сонаправлены они или направлены противоположно.
Измерительный прибор – акселерометр. (В ЕГЭ по физике есть вопросы, каким прибором что измеряют.)
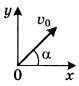
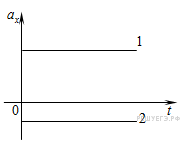
График ускорения – зависимость проекции ускорения от времени:
График ускорения при равноускоренном прямолинейном движении – прямая, параллельная оси времени (1, 2).
Чем дальше график от оси времени (2), тем больше модуль ускорения.
Мгновенная скорость – скорость в данный момент времени или в данном месте пространства .
Скорость при равноускоренном прямолинейном движении.
В векторном виде,
в проекции на ось OX,
с учетом знака ускорения («+» разгон, «-» торможение):

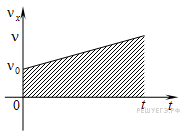
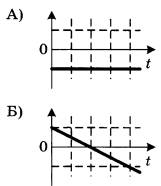
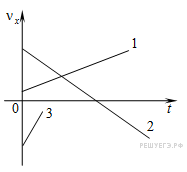
График мгновенной скорости – зависимость проекции скорости от времени.
График скорости при равноускоренном прямолинейном движении – прямая (1, 2, 3). Если график располагается над осью времени, то тело движется по направлению оси ОХ.
Чем больше угол наклона графика (3), тем больше модуль ускорения.
Если график пересекает ось времени (2), то на первом этапе тело тормозило, в какой-то момент скорость его стала равной нулю, и далее тело двигалось ускоренно в противоположную сторону.
Геометрический смысл перемещения
На графике А изображена постоянная отрицательная характеристика, остающаяся неизменной на всем времени полета камня. Среди перечисленных физических величин этому соответствует ускорение свободного падения, которое направлено к земле и тормозит вертикальный взлет камня.
На графике Б приведена физическая характеристика, которая линейно убывает с положительного до отрицательного значения. Этому соответствует вертикальная составляющая скорости полета камня, т.к. его торможение происходит на постоянную величину ускорения свободного падения.
Движение тела, брошенного под углом к горизонту (бросок)
Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом к оси ОХ (рис. 1).
Рис. 1. Тело бросили под углом к горизонту
Классическая постановка задач на подобную тематику: тело бросили под углом к горизонту с начальной скоростью , найти различные параметры движения.
Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).
Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)
Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( (м/ ), а на ось OY ( (м/ ).
Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.
Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)
Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим и . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( ), можем найти значения необходимых нам проекций:
Вернёмся к рисунку 2. Попробуем найти полное время полёта ( ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:
— т.к. время движения от точки А до B, и от B до C одинаково. Тогда:
Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( ).
Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время :
А с учётом (1) и (5):
Перейдём к максимальной высоте полёта ( ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( ) в течение времени , формируем уравнение:
Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.
Рис. 4. Тело бросили под углом к горизонту (конечная скорость)
Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:
Найдём компоненты вектора . Т.к. движение вдоль оси OX равномерное, значит, , используя (1):
Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время , тогда:
Используя (5), получим:
Подставим (12) и (13) в (10):
Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом .
Вывод:
- для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
- представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).
Способ измерения проекций горизонтальной составляющей вектора угловой скорости вращения земли для определения азимутального направления (компасирования)
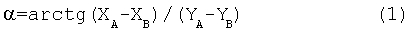
Владельцы патента RU 2300078:
Изобретение относится к области навигации и может быть использовано при создании гироскопических приборов на базе динамически настраиваемого гироскопа (ДНГ) в морской, воздушной, наземной, скважинной навигации. Способ определения азимутального направления (компасирования) основан на том, что в процессе эксплуатации производится автоматическая настройка резонансной частоты ДНГ путем модуляции переменного сигнала ДУ по одной оси сигналом прямоугольной формы частотой fт и измерением реакции ДНГ от этого сигнала по другой оси. Частоту fгм питания привода гиромотора последовательными приближениями меняют до тех пор, пока реакция ДНГ на сигнал частотой fт не станет равной нулю. Это означает, что осуществлена динамическая настройка: fгм=fрез, подвес безмоментен, его результирующая жесткость равна нулю. Техническим результатом является повышение точности определения. 1 ил.
Изобретение относится к области навигации и может быть использовано при создании азимутального корректора на базе динамически настраиваемого гироскопа (ДНГ) в морской, воздушной, наземной, скважинной навигации.
Известен способ определения азимутального направления на базе динамически настраиваемого гироскопа (ДНГ), работающего в режиме двухосного датчика угловой скорости (ДУС), измеряющего горизонтальную составляющую вектора угловой скорости вращения Земли, с вертикальной ориентацией оси кинетического момента с автокомпенсацией уходов гироскопа поворотами 0-180°. Способ принят за прототип и описан в статье Г.В.Попов, А.А.Наумов, А.И.Сорокин «Исследование возможности построения наземного гирокомпаса на ДНГ по схеме ДУС.» Сборник статей и докладов. IV Санкт-Петербургская международная конференция по интегрированным навигационным системам. ГНЦ РФ ЦНИИ «Электроприбор». Санкт-Петербург, 1997 г., с.200.
Принцип автокомпенсации уходов гироскопа поворотами 0-180° описан в монографии С.М.Зельдович, М.И.Малтинский, И.М.Окон, Я.Г.Остромухов «Автокомпенсация инструментальных погрешностей гиросистем». – Л.: Судостроение, 1976 г.
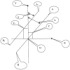
Принцип построения способа, принятого за прототип, изображен на чертеже.
АВ – модель азимута в координатах осей гироскопа XY. Положение равновесия точки А, В.
Ω – угловая скорость вращения Земли,
ϕ – широта места.
Пусть составляющие дрейфов ДНГ (град/ч): ωх≠ωу≠0.
На плоскости XY (·) А при первоначальном положении прибора и (·).
Заметим, что на плоскости XY ωx и ωу не изменили своего положения после поворота, т.к. они привязаны к осям, точка С (середина отрезка АВ) характеризует собственные уходы:
В то же время ( Ωcosϕ×Кдм) изменило свой знак.
Практически этим приемом определяют Кдм:
Приведем уравнения применительно для вышеописанного приема:
α – азимут корпуса прибора, рад,
α1 -угол разворота системы относительно корпуса, рад,
Ωз – угловая скорость вращения Земли, град/час,
ϕ – широта места,
Ωx, Ωу – проекции угловой скорости на оси платформы.
Для исключения постоянных составляющих дрейфов ДНГ проводятся измерения в двух различных азимутальных ориентациях. Это – две противоположные азимутальные ориентации, например
Для эффективности описанного способа важна кратковременная нестабильность дрейфов ДНГ за время работы в обеих ориентациях. Конструкция системы и ДНГ должна обеспечивать стабильные дрейфы при разных ориентациях гироскопа относительно корпуса и относительно Земли.
В результате постоянные составляющие дрейфов ДНГ могут быть исключены (с учетом сделанного выше замечания):
α – азимутальная ориентация осей гироскопа.
Вектор АВ – графическое моделирование направления меридиана.
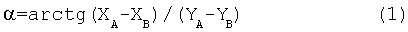
Для задач компасирования важна не стабильность ωx и ωу, а стабильность угла α. И если даже ωx и ωу изменились (точка C1 характеризует измененные собственные уходы С1x=ω1x, С1y=ω1y), угол α сохраняется (см. чертеж).
Важно только, чтобы ωx и ωу не изменялись в процессе поворота 0-180°, чтобы отсутствовал т.н. “кратковременный тренд”. Главный результат – стабильность определения меридиана (угла α) во время одного пуска, от пуска к пуску. Отметим, что имеется способ исключения “кратковременного тренда” из показаний прибора.
Поясним физику процессов при поворотах 0-180° град.
Моменты, связанные с корпусом, поворачиваются, поворачивается датчик моментов (ДМ), поворачивается система координат, т.е. моменты в системе координат не изменяют своего направления. В свободном гироскопе поворот моментов приведет к изменению знака собственного ухода в инерциальном пространстве. В случае ДУС прецессии нет, а момент остался прежний. Относительно системы координат изменил направление вектор вынужденного вращения Ωcosϕ и гироскопический момент, вызванный им, тоже изменил свое направление. Это дает возможность отличить вектор собственных моментов от вектора гироскопических моментов, вызванных вращением Земли. В ДУС мы анализируем не угол ухода, а только моменты.
Данная схема построения гирокомпаса (ГК) имеет следующие преимущества:
– ДНГ работает в ориентации, оптимальной с точки зрения минимизации вредных моментов от дебаланса и квадратурных моментов;
– температурные дрейфы ДНГ в этой ориентации также проявляются в наименьшей степени;
– возможен быстрый разворот ДНГ в новую азимутальную ориентацию вокруг оси собственного кинетического момента гироскопа;
– ДНГ расположен на поворотной платформе строго симметрично относительно оси вращения; наличие двух измерительных осей ДНГ в принципе позволяет вычислять значение азимута по измерениям двухосного ДУС в одной азимутальной ориентации;
– при точечных измерениях в положенииях 0-180° происходит автокомпенсация корпусных моментов ДНГ;
– представляется возможность сокращения времени определения азимута, поскольку динамика наземного ГК не связана с режимом незатухающих колебаний;
– в данной схеме все значимые инструментальные погрешности наблюдаемы при программных ориентациях и вращениях платформы, то есть существует принципиальная возможность определения в каждом запуске основных инструментальных погрешностей, а также возможность реализации эксплуатационного автономного режима калибровки;
– в данной схеме точность зависит от чувствительности гироскопа и от стабильности ωx и ωу за время поворота 0-180° (так называемый «кратковременный тренд»).
Прибор имеет привод разворота корпуса ДНГ вокруг оси Н, устройства питания и управления приводом и устройства для фиксации положений 0 и 180°. Программа управления процедурой поворотов, установки, измерений вводится в контроллер. Информация о токах датчиков момента ДНГ в положениях 0°, 180° ХА, ХВ, УA, YB также вводится в контроллер. По этой информации контроллер вычисляет азимут прибора в соответствии с выражением (1).
Приведенные выше простейшие зависимости и процедуры для исключения постоянных составляющих дрейфов ДНГ получили широкое распространение в силу простоты их реализации чисто аппаратными средствами, например, в контроллерах. Современная вычислительная техника позволяет реализовать способы исключения не только постоянных составляющих дрейфов ДНГ, но и их изменчивости во времени.
Для использования в навигации ДУС на базе ДНГ обладают рядом преимуществ по сравнению с другими гироскопическими чувствительными элементами (ГЧЭ), в том числе по сравнению с доступными и распространенными поплавковыми приборами. Кроме общих положений о технологичности конструкции, отсутствия поддерживающей жидкости, что влечет за собой необходимость в большом количестве функциональных элементов, ДНГ имеет следующие свойства:
– возможность функционирования в широком диапазоне температур;
– малое время готовности прибора;
– малая потребляемая мощность;
– рациональное использование внутреннего объема гироблока благодаря наличию внутреннего карданова подвеса, обеспечивающего меньшие габариты и массу;
– большое расстояние между приводом и ротором, а следовательно, малое влияние тепловыделения в приводе на точность ДНГ;
– высокая чувствительность торсионного подвеса, не имеющего сухого трения.
Для получения требуемых точностей определения азимута необходимы высокоточные ДНГ. В частности, для ДУС погрешность измерения проекций угловой скорости вращения Земли при определении азимута с погрешностью 1 дуг.мин должна лежать в пределах
Купр – «упругая» крутизна, 1/2(а+b-с)(2πfгм) 2 – «инерционная» крутизна,
Если Мдр постоянен, то он при поворотах 0-180° компенсируется по аналогии с ωх(у). Однако К – велико, а угол β непостоянен и зависит от наводки в цепи обратной связи. Все это приводит к значительной нестабильности в определении азимутального направления (ΔА). Несмотря на значительные преимущества схемы ДНГ-ДУС, экспериментально определенная настабильность ΔА в схеме определения азимутального направления ДНГ в режиме ДУС с автокомпенсацией поворотами системы координат 0-180° составила по причине описанного выше механизма нарушения динамической настройки:
в пуске – 10÷20 дуг.мин,
от пуска к пуску – порядка 30 дуг.мин.
Таким образом, способ, принятый за прототип, имеет существенную погрешность в определении азимутального направления при нарушении динамической настройки, происходящей по различным причинам.
Чтобы исключить этот эффект, необходима точная динамическая настройка, которую необходимо проводить каждый раз перед измерением.
Способ заключается в следующем:
– переменный сигнал обмотки ДУ по одной оси ДНГ модулируют переменным сигналом прямоугольной формы частотой fт,
– производят измерение реакции ДНГ на этот сигнал по другой оси,
– частоту питания привода гиромотора fгм изменяют дискретно методом последовательных приближений до тех пор, пока сигнал частотой fт по второй оси не станет равным нулю,
– после этого датчик угловой скорости (ДУС) последовательно разворачивают вокруг оси Н в фиксированные угловые положения 0°, 180°,
– измеряют сигналы ДУС по осям X, Y в этих положениях (ХА, УА и ХВ, УВ),
– затем подвергают математической обработке полученную информацию по алгоритму
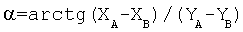
Итак, разработан способ измерения проекций горизонтальной составляющей вектора угловой скорости вращения Земли для определения азимутального направления α (компасирования), точность которого не зависит от несоответствия скорости вращения гироскопа скорости динамической настройки.
Способ, использующий перекрестное влияние одной оси на другую, который предполагает подачу на одну (первую) из обмоток ДМ дополнительного переменного сигнала прямоугольной формы частотой fт и измерение реакции от этого сигнала на второй обмотке ДМ. Величина частоты fт должна обеспечить окончание переходного процесса цепи ДУ-ДМ, при этом предполагает питание привода гиромотора осуществлять частотой fгм, причем частота fгм изменяется дискретно, пока сигнал частотой fт на второй обмотке ДМ не станет равным нулю.
Осуществление этой процедуры производится посредством контроллера по записанной в нем программе.
Проведенные испытания показали, что в схеме определения азимутального направления ДНГ в режиме ДУС с автокомпенсацией моментов поворотами системы координат 0-180° по вышеприведенной методике настабильность ΔА в определении азимута составила:
от пуска к пуску – не более 1 дуг.мин.
Способ измерения проекций горизонтальной составляющей вектора угловой скорости вращения Земли для определения азимутального направления α (компасирования), заключающийся в том, что датчик угловой скорости (ДУС) последовательно разворачивают вокруг оси Н в фиксированные угловые положения 0°, 180°, измеряют сигналы ДУС по осям X, Y в этих положениях (ХA, YA и ХB, YB), затем полученную информацию подвергают математической обработке по алгоритму
отличающийся тем, что в процессе эксплуатации после запуска динамически настраиваемого гироскопа (ДНГ) перед измерением сигналов ДУС по одной оси ДНГ переменный сигнал обмотки ДУС модулируют переменным сигналом прямоугольной формы частотой fт, затем производят измерение реакции ДНГ на этот сигнал по другой оси, при этом частоту питания привода гиромотора fгм изменяют дискретно методом последовательных приближений до тех пор, пока сигнал частотой fт по второй оси не станет равным нулю.


Позвольте представиться. Меня зовут Татьяна. Я уже более 8 лет занимаюсь психологией. Считая себя профессионалом, хочу научить всех посетителей сайта решать разнообразные задачи. Все данные для сайта собраны и тщательно переработаны для того чтобы донести как можно доступнее всю необходимую информацию. Перед применением описанного на сайте всегда необходима ОБЯЗАТЕЛЬНАЯ консультация с профессионалами.













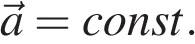
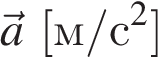 ) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.
) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.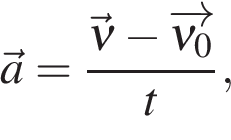

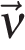 — скорость тела в момент времени t.
— скорость тела в момент времени t.
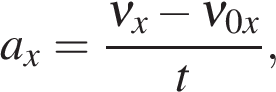

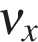 — проекция скорости тела на ось Ox в момент времени t.
— проекция скорости тела на ось Ox в момент времени t.
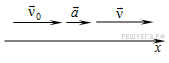
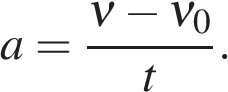
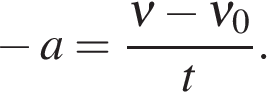
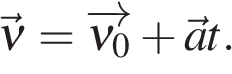
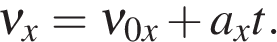


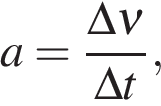
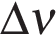 — изменение скорости за время
— изменение скорости за время