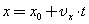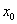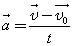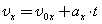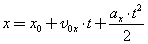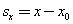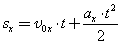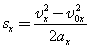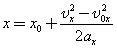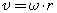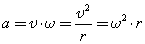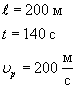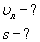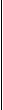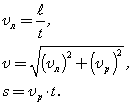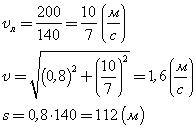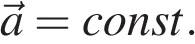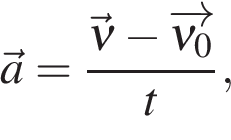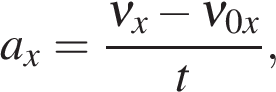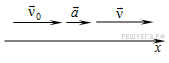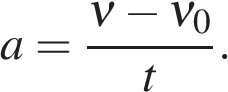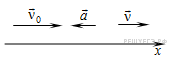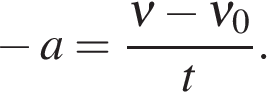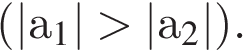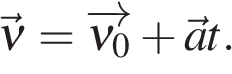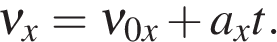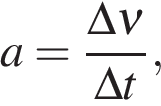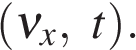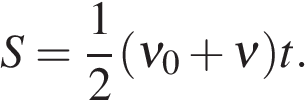Татьяна Ефимова предлагает статью на тему: "проекция скорости на ось" с детальным описанием.
Содержание
- 1 Скорость прямолинейного равноускоренного движения
- 2 Проекция скорости на ось
- 3 Методы, способы, приемы решения физических задач
- 4 1. МЕХАНИКА 1.1. Кинематика
- 5 Савельев И.В. Курс общей физики, том I
- 6 Большая Энциклопедия Нефти и Газа
- 7 Большая Энциклопедия Нефти и Газа
- 8 График проекции скорости в зависимости от времени.
- 9 Проекции скорости на оси координат
- 10 Чему равна проекция скорости тела? (1 июля 2011)
Скорость прямолинейного равноускоренного движения
Проекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле:
Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t.
То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело в данной точке.
- Представим зависимость скорости от времени при равноускоренно движении в виде графика.
Графиком уравнения Vx=V0x+ax*t будет прямая линия. Расположение этой лини в системе координат будет определяться значениями ax b V0x.
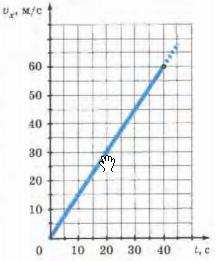
График проекции скорости тела при нулевой начальной скорости
На следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел нулевую скорость, и двигалось равноускоренно и прямолинейно с ускорением ax=1,5 м/(с^2) в течение 40 секунд.
Так как изначально скорость была нулю, то уравнение примет следующий вид
Для построения графика достаточно взять пару точек. Выберем момент времени
t=40, тогда Vx= ax*t =1,5*40 = 60
Отметим эти точки на графике и соединим их прямой.
Так как ускорение положительное, то график образует с осью Ох острый угол.
График проекции скорости тела при ненулевой начальной скорости
Теперь посмотрим, как будет выглядеть график вектора проекции скорости, при начальной скорости тела отличной от нуля.
В этом случае график будет описываться функцией Vx=V0x+ax*t.
На следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел скорость Vx=10, и двигалось равноускоренно и прямолинейно с ускорением ax=1,4 м/(с^2) в течение 4 секунд.
Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость.
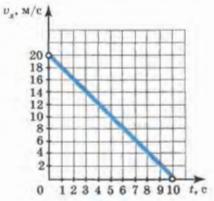
График проекции скорости тела при торможении
Если бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол.
Ниже представлен график такой ситуации.
Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось.
Нужна помощь в учебе?
Предыдущая тема: Прямолинейное равноускоренное движение и ускорение
Следующая тема:   Перемещение при прямолинейном равноускоренном движении
|
Все неприличные комментарии будут удаляться. Проекция скорости на ось  
Материалы к зачету по теме “Основные законы механики “1. Механическое движение. Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле: где 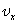 — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи. — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.
Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны. Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется. 2. Основная задача механики Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость. Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле: Координату тела находят по формуле: Проекцию перемещения находят по формуле: Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0. Значение проекции перемещения при равноускоренном движении можно определить также по формуле:
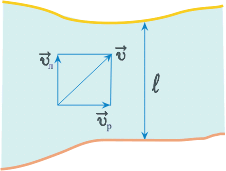
При вычислениях по приведенным формулам знаки проекций векторов 3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω. Связь между линейной и угловой скоростью выражается формулой: где r — радиус окружности. Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения. Пример решения задачи: 1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м. Решите задачи самостоятельно: 1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки 2. 9 км/ч = . м/с; 10 м/с = . км/ч; 8 км/с = . км/ч, 54 км/ч = . м/с. 3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением; Методы, способы, приемы решения физических задачПроекция вектора скорости положительна, а проекция вектора ускорения – отрицательна. Знак проекции вектора определяется знаком косинуса угла α. Из уравнения координат тела как функции времени можно получить уравнение для проекции на ось Х вектора скорости как функции времени путём его дифференцирования по времени. Vх=dx/dt=V0х+ ахt. Наиболее общей задачей на движение тела в поле силы тяжес ти (гравитационном поле) является задача о движении тела, брошенного под углом к горизонту. Задача: Девочка бросает мяч с балкона, находящегося на высоте h от поверхности земли, под углом α к горизонту со скоростью V0. Определить время полета мяча до земли, дальность полёта (координату Xmax точки падения), наибольшую высоту полёта мяча над землёй (максимальное значение координаты Уmax мяча) и скорость мяча в момент его падения на землю. (рис 7) Решение задачи начинается с выбора начала отсчёта, с которым совмещают начало системы координат ХОУ. Удобно начало отсчета и связанное с ним начало координат выбрать на поверхности земли под балконом, направив оси Х и У соответственно горизонтально и вертикально. Отмечаем на оси У начальную координату мяча У0 = h, направляем вектор начальной скорости V0 под углом α к горизонту и изображаем траекторию полёта мяча, которая, представляет собой параболу. Точка пересечения параболы с осью Х определит координату Xmax, значение которой даст дальность полёта мяча. Наибольшая высота полёта мяча определится значением координаты Уmax вершины параболы. Для составления уравнений движения Х=Х (t) и У=У (t) имеет смысл записать составляющие этих уравнений: Через время tп (время полёта мяча) координаты мяча примут значения: Х =Хmax, у = 0. Тогда уравнения примут вид: Хmax=V0 (cosα) tп; 0=h+ (V0sinα) tп-gtп2/2. Решая последнее квадратное уравнение, находим время полёта мяча tп. tп= [V0sinα+ (V02sin2α+ 2gh) 1/2] /g, которое имеет только одно значение. Второе – отрицательное значение tп, которое следует из решения квадратного уравнения, не возможно. Здесь и далее корень квадратный из числа записывается как это число в степени ½. Подставив значение tп в уравнение определим дальность полёта мяча Хmax. Хmax=V0 (cosα) =V0 (cosα) [V0 sin α + (V02 sin2α + 2gh) 1/2] /g. В верхней точке траектории мяча высота его полёта максимальна, а проекция скорости на ось ОУ равна нулю. Для продолжения решения необходимо перейти к уравнениям проекций скорости V на оси Х и У как функциям времени. Взяв производные по времени от уравнений движения, получаем: Первое уравнение показывает, что вдоль оси ОХ мяч летит равномерно с постоянной скоростью, не зависящей от времени. Движение мяча вдоль оси ОУ является равнопеременным (при движении до верхней точки полёта – равнозамедленным, а затем становится равноускоренным). В момент времени tв (время полёта мяча до верхней точки) проекция скорости Vy становится равной нулю, а координата У принимает максимальное значение уmax. уmax=h+ (V0sinα) tв – gtв2/ 2. Определив время tв, tв= (V0sinα) /g, подставляем его значение в уравнение и определяем уmax – максимальную высоту полёта мяча. уmax=h+ (V02sin2α) /2g. Для определения скорости мяча в момент падения (время tп) необходимо определить значения проекций этой скорости Vx и Vy в этот момент. Vy =V0sinα-gtп =V0 sinα – g [V0 sin α + (V02 sin2α + 2gh) 1/2] /g Скорость мяча в момент падения V определится по теореме Пифагора: Проекция Vy будет отрицательной, но будучи возведённой в квадрат даст положительное значение. Следует помнить, что вектор скорости в любой точке направлен по касательной к траектории движения. Решение задач на движение тела, брошенного вертикально вверх или вниз, или свободно падающее (здесь угол α = 90о) сводится к составлению только одного уравнения: У=h+V0t – gt2/2. Уравнение записано для случая бросания тела вертикально вверх с высоты h. Ось У направлена вверх, начало координат совпадает с уровнем земли. Если тело брошено горизонтально (α = 0о), то уравнения движения записанные в начале решения принимают вид: Если в задаче описывается движение двух тел, то нужно составлять уравнения движения для каждого тела. Если в какой-то момент времени одно тело догоняет другое или они встречаются (сталкиваются), то это означает, что в этот момент времени они приобретают одинаковые координаты Х и У. Решение задач по динамике. При решении используются понятия проекций вектора силы и ускорения на координатную ось. Основное уравнение динамики или второй закон Ньютона, записанный в форме проекций сил и ускорения на координатную ось ОХ, выглядит так: ΣFix=max. Умение составлять такие уравнения является основой для решения динамических задач, в которых, требуется определить ускорение в движении тела или системы тел и пассивные силы (силы трения, натяжения связывающих тела нитей, реакций опор). Задача: Cистема из двух грузов массами m1 и m2 (рис.8) находится в лифте. движущемся вверх с ускорением а. Найти силу натяжения Т нити, если коэффициент трения между грузом m1 и опорой равен μ. Грузы связаны нерастяжимой нитью, поэтому ускорения грузов относительно стола одинаковы по величине и равны а’. В неподвижной системе отсчёта ускорение груза m2 направлено по вертикали и равно а2 = а’ – а. Ускорение груза m1 имеет две составляющие: вертикальную а1в = а и горизонтальную а1г = а’. Запишем второй закон Ньютона для движения каждого из грузов в виде проекций сил и ускорений на координатные оси: для первого груза массой m1 ОХ: Т-Fтр=m1a1г; ОУ: N-m1g= m1a1в; Fтр=μN для второго груза массой m2 ОУ: m2g – T = m2a2 или Решая систему, состоящую из двух уравнений, получаем выражение для силы натяжения нити Т=m1m2 (g+a) (1+μ) / (m1+m2). Применение координатного метода к статическим задачам. Координатный метод широко используется при решении статических задач. Если тело находится в равновесии под действием сходящейся системы сил, линии действия которых пересекаются в одной точке, то условие равновесия записывается в виде следующих соотношений: ΣFix=0 и ΣFiy=0 для плоской системы сходящихся сил, вектора которых лежат в одной плоскости. Если система сходящихся сил является пространственной, то к выше приведённым уравнениям добавляется уравнение ΣFiz=0. Задача: Заряженный алюминиевый шарик радиуса r, подвешенный на тонкой нерастяжимой нити, находится между двумя параллельными вертикальными пластинами, расстояние между которыми d. Пространство между пластинами заполнено керосином. Каков заряд шарика, если при подаче на пластины напряжения U угол отклонения нити равен α? (рис.9) 1. МЕХАНИКА
|
|||||||
Главная редакция физико-математической литературы
Механика, колебания и волны,
КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I
Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.
Предисловие к четвертому изданию
При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.
Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.
Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.
Ноябрь 1969 г. И. Савельев
Из предисловия к четвертому изданию
Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.
При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.
Большая Энциклопедия Нефти и Газа
Проекция – угловая скорость
Проекции угловой скорости на неподвижные оси координат и на оси координат, неизменно связанные с телом. Наиболее прямой путь для получения выражений проекций угловой скорости через эйлеровы углы заключался бы в использовании формул (9.6) на стр. [1]
Проекции угловой скорости со, cor ox вынесены за знаки сумм, так как они не зависят от точек тела, по которым ведется суммирование. Суммы в ( Г) представляют собой соответственно осевой Jx и центробежные JXy, Jxz моменты инерции. [2]
Проекции угловой скорости ш на оси х, у, г, связанные с телом, выражаются через углы Эйлера ( фиг. [3]
Проекции угловой скорости на неподвижные оси координат и на оси координат, неизменно связанные с телом. Наиболее прямой путь для получения выражений проекций угловой скорости через эйлеровы углы заключался бы в использовании формул (9.6) на стр. [4]
Проекции угловой скорости м на оси х, у, z, связанные с телом, выражаются через углы Эйлера ( фиг. [5]
Проекции угловой скорости со на оси х, у, z, связанные с телом, выражаются через углы Эйлера ( фиг. [6]
Проекции угловой скорости сот, юу, ю2 вынесены за знаки сумм, так как они не зависят от точек тела, по которым ведется суммирование. Суммы в ( Г) представляют собой соответственно осевой J х и центробежные / яр, У хг моменты инерции. [7]
Проекции угловой скорости cog, to, coj определяются по формулам Эйлера. [8]
Проекция угловой скорости на ось z, перпендикулярную плоскости чертежа, UOAZ 0, следовательно, кривошип вращается против часовой стрелки. [9]
Проекции угловой скорости &x , eor coz вынесены за знаки сумм, так как они не зависят от точек тела, по которым ведется суммирование. Суммы в ( Г) представляют собой соответственно осевой Jx и центробежные Jxy, Лг моменты инерции. [10]
Проекции угловой скорости сох , tov, to, вынесены за знаки сумм, так как они не зависят от точек тела, по которым ведется суммирование. Суммы в ( Г) представляют собой соответственно осевой J и центробежные Лу, Лг моменты инерции. [11]
Проекции угловой скорости твердого тела , вращающегося вокруг неподвижной точки О, на неподвижные координатные оси Охуг выражаются формулами ох 2 /; aat2; г гз. [12]
Пусть проекции угловых скоростей получили малые приращения 8ь 8з, 8з, малые настолько, что их квадратами и произведениями можно пренебрегать. [13]
Найти проекции угловых скоростей объекта на оси связанной с ним системы координат, а для каждого элемента ГИО ( ротора и кожуха) найти проекции угловых скоростей КА и гироскопа на жестко связанные с ним оси координат. [14]
Если проекции угловой скорости шж , шу и шг в данный момент известны, то по этим формулам легко найти проекции скорости v любой точки тела в этот момент и, следовательно, определить модуль и направление этой скорости. [15]
Большая Энциклопедия Нефти и Газа
Проекция – вектор – скорость
Проекция вектора скорости на направление вектора угловой скорости есть величина постоянная, не зависящая от выбора полюса. [1]
Проекция вектора скорости на плоскость z const поворачивается на угол я / 2 при изменении z от 0 до оо, в то время как его величина экспоненциально затухает. [2]
Проекции вектора скорости на оси координат равны производным от проекций точки на данную ось, или просто производным от координат движущейся точки. Обычно говорят короче, например: скорость самолета имеет две составляющие – горизонтальную и вертикальную. [3]
Поскольку проекции вектора скорости на одну какую-либо ось координат имеют одинаковое направление, то достаточно только выполнять их алгебраическое сложение. [4]
Если проекция вектора скорости на плоскость, перпендикулярную оси ствола трубки, совпадает с биссектрисой угла, образованного нитями, то условия охлаждения обеих нитей в потоке, а следовательно, и сопротивления нитей будут одинаковыми. [5]
Если проекции вектора скорости скольжения УСН разложить на составляющие – вдоль проекций контактных линий гск. [6]
Поскольку проекция вектора скорости движения выделенного элемента на ось Z пренебрежимо мала, то соответственно малы и ускорения в этом направлении. [7]
Следовательно, проекция вектора скорости на координатную ось равна производной по времени соответствующей координаты движущейся частицы. [8]
Чтобы найти проекции вектора скорости на эти направления, можно воспользоваться указанным выше свойством проекции вектора скорости на произвольную неподвижную ось, или же непосредственно исходить из формул преобразования вектора при переходе от одной системы координат к другой. Мы применим здесь оба способа. [9]
Чему равны проекции вектора скорости точки на оси вых координат. [10]
Чему равны проекции вектора скорости точки на естественные оси. [11]
Итак, проекции вектора скорости точки на неподвижные оси координат равны первым производным по времени от соответствующих координат точки. [12]
Взяв – проекции векторов скорости молекул на линию их центров и перпендикулярно ей, получим для каждой молекулы по две составляющие: ( ylc, i ijj, ( УЗС уз 1) – Если тангенциальные силы в момент столкновения отсутствуют, то составляющие УЦ и y2j при столкновении не изменятся. Остается рассмотреть изменение составляющих, направленных вдоль линии центров. [13]
Следовательно, проекция вектора скорости маятника Фуко на плоскость Оху вращается с постоянной отрицательной угловой скоростью, равной по модулю со sin ср. Это обозначает, что с такой угловой скоростью вращается мгновенная плоскость колебаний маятника Фуко. [14]
При отклонении проекции вектора скорости от указанного направления изменяются коэффициенты теплоотдачи нитей, вследствие чего изменяется их температура и сопротивление. В измерительной диагонали моста появляется напряжение разбаланса, которое через переключатель рода работы П1 подается на вибропреобразователь ВП. [15]
График проекции скорости в зависимости от времени.
Равнопеременное движение по прямой.
3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением:
3.1.2. Ускорение ( 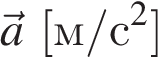
В векторном виде:
где
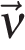 — скорость тела в момент времени t.
— скорость тела в момент времени t.
В проекции на ось Ox:
где
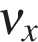 — проекция скорости тела на ось Ox в момент времени t.
— проекция скорости тела на ось Ox в момент времени t.
Знаки проекций зависят от направления векторов и оси Ox.
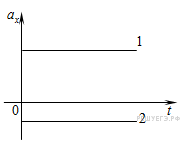
График проекции ускорения от времени.
При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.):
Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения
Скорость при равнопеременном движении.
В векторном виде:
В проекции на ось Ox:
Для равноускоренного движения:
Для равнозамедленного движения:
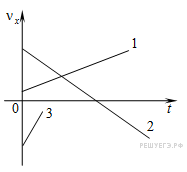
График проекции скорости в зависимости от времени.
График проекции скорости от времени — прямая линия.
Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox.
Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения;
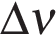 — изменение скорости за время
— изменение скорости за время 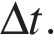
Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).
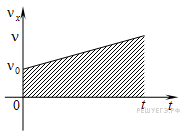
3.1.6. Геометрический смысл площади под графиком в осях
Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом.
На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9825 –
 или читать все.
или читать все.
185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Проекции скорости на оси координат
Проекции скорости на координатные оси равны первым производным от координат x, y, z по времени:
Вектор мгновенной скорости и его модуль V через
проекции скорости v , v , v , можно записать как:
v v x i v y j v z k
v
 v 2 x v 2 y v 2 z
v 2 x v 2 y v 2 z
В процессе движения материальной точки модуль и направление её скорости в общем случае изменяются.
Ускорение характеризует быстроту изменения скорости с течением времени.
Ускорение равно изменению скорости за единицу времени.
Ускорение измеряется в м/с 2 .
Среднее ускорение
Среднее ускорение за промежуток времени t равно
Чему равна проекция скорости тела? (1 июля 2011)
Источник: ЕГЭ 2011, О. Ф. Кабардин, С. И. Кабардина, В. А. Орлов.
Помогите решить задачу, не сходится ответ, в ответах 0, у меня получается 3, хотя бы по порядку, что и как находим, а решу сам.
- версия для печати
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Комментарии
Один из вариантов:
v = Δx/Δt = x / = (1 + 4t − 2t 2 ) / = 4 − 4t.
В уравнение скорости:
подставляем t = 1 c.
Второй вариант предложите сами.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
1) Можно через координаты, построив график зависимости x от t. У нас есть уравнение координаты, значит, xo = 1 м, так как t = 1 c, то подставим в уравнение координаты и получим: x = 1 + 4 × 1 − 2 × 1 × 1 = 3 м, то есть пройденный путь Δx = x − xo, или Δx = 3 − 1 = 2 м.
2) Можно найти путь, пройденный телом, по формуле Δx = vot − (at 2 )/2, или Δx = 4 × 1 − (4 × 1 × 1)/2 = 2 м.
Теперь найдём скорость.
1) Можно по формуле Δx = (v 2 − vo 2 ) / (−2a) (минус, так как торможение, что видно из уравнения) или v = √(vo 2 − 2aΔx), то есть v = (4 × 4 − 2 × 4 × 2) = 0 м/c.
2) Можно по формуле Δx = (v + vo)/2, или v = (2Δx − vot)/t, то есть v = (2 × 2 − 4 × 1)/1 = 0 м/с.

Позвольте представиться. Меня зовут Татьяна. Я уже более 8 лет занимаюсь психологией. Считая себя профессионалом, хочу научить всех посетителей сайта решать разнообразные задачи. Все данные для сайта собраны и тщательно переработаны для того чтобы донести как можно доступнее всю необходимую информацию. Перед применением описанного на сайте всегда необходима ОБЯЗАТЕЛЬНАЯ консультация с профессионалами.