Проекция боковой стороны

Проекция боковой стороны

пУОПЧБОЙС ТБЧОПВЕДТЕООПК ФТБРЕГЙЙ ТБЧОЩ 10 Й 24, ВПЛПЧБС УФПТПОБ ТБЧОБ 25. оБКДЙФЕ ЧЩУПФХ ФТБРЕГЙЙ.

вПМШЫЕЕ ПУОПЧБОЙЕ РТСНПХЗПМШОПК ФТБРЕГЙЙ ЧДЧПЕ ВПМШЫЕ ЕЈ НЕОШЫЕЗП ПУОПЧБОЙС, Б ВПЛПЧЩЕ УФПТПОЩ ТБЧОЩ 4 Й 5. оБКДЙФЕ ДЙБЗПОБМЙ ФТБРЕГЙЙ.

вПЛПЧБС УФПТПОБ ТБЧОПВЕДТЕООПК ФТБРЕГЙЙ ТБЧОБ 41, ЧЩУПФБ ТБЧОБ 40 Й УТЕДОСС МЙОЙС ТБЧОБ 45. оБКДЙФЕ ПУОПЧБОЙС.

оБКДЙФЕ ЧЩУПФХ ФТБРЕГЙЙ УП УФПТПОБНЙ 10, 10, 10 Й 26.

уФПТПОЩ ФТБРЕГЙЙ ТБЧОЩ 17, 17, 17 Й 33. оБКДЙФЕ ЧЩУПФХ ФТБРЕГЙЙ.

тЕЫЕОЙЕ

уФТБОЙГБ: 1 2 3 4 5 6 7 >> [чУЕЗП ЪБДБЮ: 53]

рТПЕЛФ ПУХЭЕУФЧМСЕФУС РТЙ РПДДЕТЦЛЕ Й .

Проекция боковой стороны

рТПЕЛГЙС ВПЛПЧПК УФПТПОЩ ТБЧОПВЕДТЕООПК ФТБРЕГЙЙ ОБ ВПМШЫЕЕ ПУОПЧБОЙЕ ТБЧОБ a , УТЕДОСС МЙОЙС ФТБРЕГЙЙ ТБЧОБ b , Б ПУФТЩК ХЗПМ РТЙ ПУОПЧБОЙЙ ТБЧЕО 45 o . оБКДЙФЕ ТБДЙХУ ПЛТХЦОПУФЙ, ПРЙУБООПК ПЛПМП ФТБРЕГЙЙ.
фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

рХУФШ ABCD — ТБЧОПВЕДТЕООБС ФТБРЕГЙС У ПУОПЧБОЙСНЙ AD>BC , ADC = 45 o , CH — ЧЩУПФБ ФТБРЕГЙЙ, R — ТБДЙХУ ПЛТХЦОПУФЙ, ПРЙУБООПК ПЛПМП ФТБРЕГЙЙ. йЪЧЕУФОП, ЮФП РТПЕЛГЙС ДЙБЗПОБМЙ ТБЧОПВЕДТЕООПК ФТБРЕГЙЙ ОБ ВПМШЫЕЕ ПУОЧБОЙЕ ТБЧОБ РПМХУХННЕ ПУОПЧБОЙК, Ф.Е. УТЕДОЕК МЙОЙЙ ФТБРЕГЙЙ. фПЗДБ
CH=DH=a, AH= (AD+BC) = b, AC= = .
пЛТХЦОПУФШ, ПРЙУБООБС ПЛПМП ФТБРЕГЙЙ УПЧРБДБЕФ У ПЛТХЦОПУФША, ПРЙУБООПК ПЛПМП ФТЕХЗПМШОЙЛБ ACD . рП ФЕПТЕНЕ УЙОХУПЧ
R= = = = .

фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

.
фБЛЦЕ ДПУФХРОЩ ДПЛХНЕОФЩ Ч ЖПТНБФЕ TeX

йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС

web-УБКФ
оБЪЧБОЙЕ	уЙУФЕНБ ЪБДБЮ РП ЗЕПНЕФТЙЙ т.л.зПТДЙОБ
URL	http://zadachi.mccme.ru
ЪБДБЮБ
оПНЕТ	3393

рТПЕЛФ ПУХЭЕУФЧМСЕФУС РТЙ РПДДЕТЦЛЕ Й .

Проекция боковой стороны

Найдите среднюю линию и проекция боковой стороны стороны равносторонней проекции на большую основу , если боковая сторона равняется 17 см , высота – 15см , а меншая основа – 10 см.

Лучший ответ:

Проекция боковой стороны трапеции на большее основание равна Пр = sqrt (17^2 -15^2) = sqrt (17^2 -15^2) = sqrt (64) = 8Т.к. трапеция равнобокая, то и проекция второй боковой стороны на большее основание равна 8.Большее основание равно сумме меньшего основания и двух проекций боковых сторон: Б осн = 10+8+8 =26.Средняя линия трапеции равна полусумме оснований: Ср лин = (10+26)/2 = 18

Другие вопросы:

Группа туристов состоит из 6 иностранцев. Они говорят только по французки или по англиски. Три человека говорят только по англиски, два человека говорят только по французки. Сколько человек говорят на двух языках: и по-французки и по англиски?

Найдите cosx,если sinx=-0,3 и угол лежит в третьей четверти?

Найдите среднюю линию и проекция боковой стороны стороны равносторонней проекции на большую основу , если боковая сторона равняется 17 см , высота – 15см , а меншая основа – 10 см.

Ответ оставил Умник

Проекция боковой стороны трапеции на большее основание равна Пр = sqrt (17^2 -15^2) = sqrt (17^2 -15^2) = sqrt (64) = 8

Т.к. трапеция равнобокая, то и проекция второй боковой стороны на большее основание равна 8.

Большее основание равно сумме меньшего основания и двух проекций боковых сторон: Б осн = 10+8+8 =26.

Средняя линия трапеции равна полусумме оснований: Ср лин = (10+26)/2 = 18

Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Геометрия.

Найдите среднюю линию и проекция боковой стороны стороны равносторонней проекции на

Проекция боковой стороны трапеции на большее основание равна Пр = sqrt (17^2 -15^2) = sqrt (17^2 -15^2) = sqrt (64) = 8

Т.к. трапеция равнобокая, то и проекция второй боковой стороны на большее основание равна 8.

Большее основание равно сумме меньшего основания и двух проекций боковых сторон: Б осн = 10+8+8 =26.

Средняя линия трапеции равна полусумме оснований: Ср лин = (10+26)/2 = 18

как понимать: проекция боковой стороны равнобедренной трапеции на основание?

Если в трапеции ABCD провести высоты ВН и СК, то отрезки АН и DK будут проекциями боковых сторон трапеции на основание AD.

Это как-будто тень на основании AD от этих сторон, если бы свет падал из точек В и С перпендикулярно к AD.

Проекция боковой стороны

Равнобедренная трапециа. Трапеция называется равнобедренной, если ее боковые стороны равны. Свойства и признаки равнобедренной трапеции. 1. Углы при основании равнобедренной трапеции равны. 2. Диагонали равнобедренной трапеции равны. 3. Если углы при основании трапеции равны, то она равнобедренная. 4. Если диагонали трапеции равны, то она равнобедренная. 5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме основаннй. Формулы площади четырехугольника 1. Плошадь параллелограмма равна произведешпо основания на вы- соту.

2. Плошадь параллелограмма равна произведшппо его соседних сторон на сннус угла между ними.

3. Плошадь прямоугольника равна пронзведенюо двух его соседних сторон. 4. Плошадь ромба равна половине проязведения его диагоналей. 5. Плошадь трапеции равна произведению полусуммы оснований на высоту.

б. Площадь четыр6хутольника равна половине произаелення его диагоналей на синус угла между ними.

7. Формула 1йрона для чет ьника, около которого можно описать окружность: Я = 1р — оИр — Ь)1р — с 1р — Ы), где о, Ь,с, Ы — стороны етого четырехугольника, р — полупериметр, а Я — плошадь. Подобные фигуры 1. Отношение соответствующих линейных злементов подобных фигур равно козффициенту подобна

2. Отношение площадей подобных фигур равно квадрату ковффяциента подобия. Правильный многоугольник. Пусть а„— сторона правильного п-угольника, а г„и В„— ралиусы вписанной н описанной окружностей. Тогда:

а„= 2В„аш —; а„= 2 тй — г„; г„= В„° соз —. п ‘ п

У П. Влззлмегрза

Окрувшостью называется геометрическое место точек плоскости, удаленных от данной тачки, называемой центром окружности, на одно и то же положительное расстояние.

Основные свойства окружности

1. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею луги пополам.

2. Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен втой хорде.

3. Серединный перпендикуляр к хорде проходит через центр окружно- 4. Равные хорды удалены от центра окружности на равные расстояния.

5. Хорды окружности, удалйнные от центра на равные расстояния, равны.

б. Окружность симметрична относительно любого своего знамегра.

7. Дуги окружности, заключенные между параллельными хордами, равны.

8. Из двух хорд больше та, которая менее удалена от центра.

9. Диаметр есть наибольшая хорда окружности.

Замечательные свойства окружности

1. Геометрическое место точек М, из которых отрезок АВ виден под. прямым утлом (

АМВ = 90′), есть окружность с диаметром АВ без точек А и В.

2. Геометрическое место точек М, из которых отрезок АВ виден под острым утлом (лАМВ 90′), есть внутренность круга с диаметром АВ без точек отрезка АВ.

4. 1еометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных оиружностей (без концов этих дуг).

Касательная к окружности. Прямая, нмеющая с окружностью единственную общую точку, называется касательной к окружности.

1. Касательная перпендикулярна радиусу, проведйнному в точку касаняя.

2. Если прямая и, проходящая через точку иа окружности, перпендккулярна радиусу, провеайиному в эту точку, то прямая и — касательная к

Президентский ФМЛ №239

Инструменты пользователя

Инструменты сайта

Содержание

Определение

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

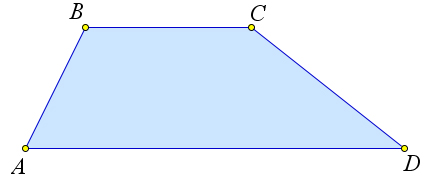
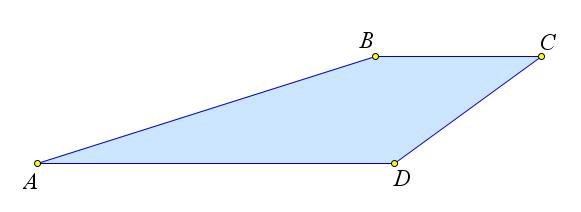
Сумма углов при боковой стороне трапеции равна $180^circ$.

Доказательство

Действительно, так как основания трапеции параллельны, а боковая сторона является секущей, то углы при боковой стороне являются внутренними односторонними углами при параллельных прямых, и, следовательно, их сумма равна $180^circ$.

Определение

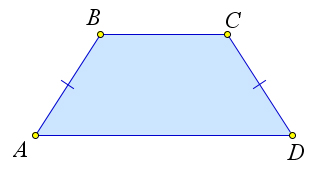
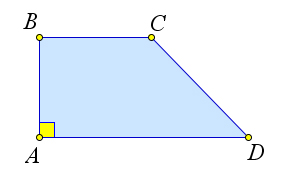
Свойства равнобедренной трапеции

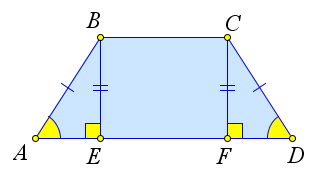
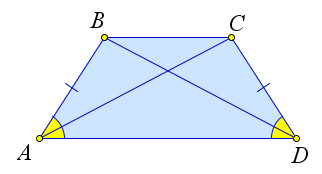
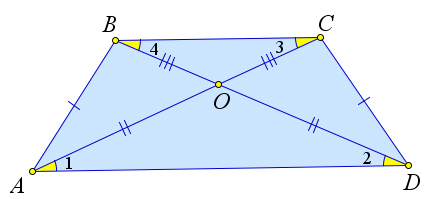
Доказательство

Докажем первый пункт теоремы.

Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.

Докажем, что $angle A=angle D$.

Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.

Треугольники $triangle ABE$ и $triangle CFD$ равны по катету и гипотенузе ($AB=CD, BE=CF$).

Следовательно, $angle A=angle D$.

Докажем второй пункт теоремы.

В равнобедренной трапеции $ABCD$ рассмотрим треугольники $triangle ABD$ и $triangle ACD$.

Они равны по первому признаку ($AB=CD$, $AD$ – общая, $angle A=angle D$ по первому пункту).

Докажем третий пункт теоремы.

Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные, а треугольники $triangle AOB$ и $triangle COD$ равны.

Действительно, во втором пункте уже было доказано, что $triangle ABD=triangle ACD$.

Следовательно, $angle 1=angle 2$, а так как они накрест лежащие с углами $angle 3$ и $angle 4$ соответственно, то $angle 3=angle 4$, что и означает, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные.

Тогда $AO=OD$ и $BO=OC$, и как следствие, $triangle AOB=triangle COD$ по третьему признаку равенства треугольников.

Докажем четвертый пункт теоремы.

Так как $triangle AEB=triangle CFD$ (по катету и гипотенузе), то $AE=FD$.

Кроме того, $EF=BC$, следовательно, $AE=dfrac$ и $AF=dfrac+BC=dfrac$.

Признаки равнобедренной трапеции

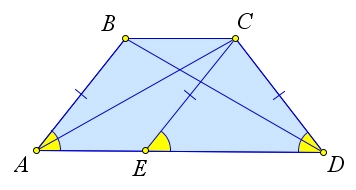
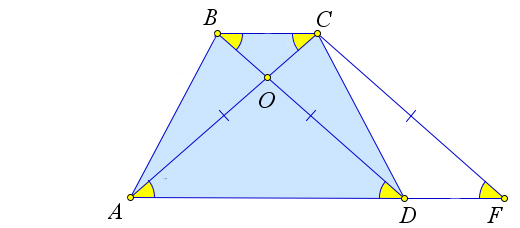
Доказательство

Докажем первый пункт теоремы.

Рассмотрим трапецию $ABCD$, в которой $angle A=angle D$.

Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.

Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.

Тогда $angle A=angle CED$, как соответственные углы.

Следовательно, $angle CED=angle D$, а тогда $triangle CED$ – равнобедренный.

А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.

Докажем второй пункт теоремы.

Рассмотрим трапецию $ABCD$, у которой $AC=BD$.

Докажем, что тогда $AB=CD$.

Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.

Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.

Тогда $triangle ACF$ – равнобедренный, так как $AC=CF$.

Следовательно $angle OAD=angle ODA$, и $triangle AOD$ – равнобедренный.

Тогда $AO=OD$ и $BO=OC$.

Следовательно, $triangle BOA=triangle COD$ по первому признаку ($angle BOA=angle COD$ – как вертикальные).

Теорема (о равнобедренной трапеции с перпендикулярными диагоналями)

В равнобедренной трапеции со взаимно перпендикулярными диагоналями высота равна средней линии.

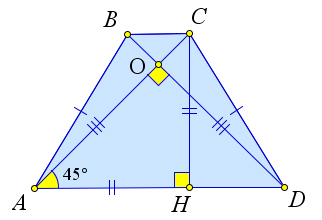
Доказательство

Рассмотрим равнобедренную трапецию $ABCD$, в которой $ACperp BD$.

Докажем, что в такой трапеции высота $CH$ равна средней линии то есть полусумме оснований.

Действительно, $triangle AOD$ – равнобедренный и прямоугольный, следовательно, $angle OAD = 45^circ$. Тогда $triangle AHC$ – равнобедренный, то есть $AH=CH$.

Проекция боковой стороны

Вопрос по геометрии:

как понимать: проекция боковой стороны равнобедренной трапеции на основание?

Ответы и объяснения 1

Если в трапеции ABCD провести высоты ВН и СК, то отрезки АН и DK будут проекциями боковых сторон трапеции на основание AD.

Это как-будто тень на основании AD от этих сторон, если бы свет падал из точек В и С перпендикулярно к AD.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат – это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи – смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Проекции треугольника, многоугольника и круга

Итак, найдя постоянную прямую чертежа, мы можем построить одну из возможных систем плоскостей проекций. Очевидно, что начало координат любой системы должно находиться на постоянной прямой чертежа. Отсюда следует, что постоянная прямая чертежа является геометрическим местом точек, фиксирующих начало координат всех возможных систем плоскостей проекций П₂, П₃.

При построении проекций четырехугольника общего положения нельзя взять четыре произвольные точки. Как только мы возьмем три точки, плоскость определится, и четвертую точку надо строить при условии, чтобы она принадлежала этой плоскости. Практически пользуются диагоналями проекций четырехугольника (рис. 115, в).

Фронтальную проекцию четырехугольника ABCD Рис. 116 строим произвольно; также произвольно строим горизонтальные проекции трех точек А₁, В₁ и С₁ треугольника A₁B₁C₁. Для построения горизонтальной проекции D₁ точки D проводим фронтальные проекции А₂С₂ и D₂B₂ диагоналей четырехугольника.

Проекции диагоналей пересекутся между собой в точке Е₂. Находим горизонтальную проекцию E₂ этой точки на горизонтальной проекции А₁С₁ будущей диагонали АС; соединяем точки В₁ и E₁ и на продолжении этой линии находим точку D₁ на вертикальной линии связи D₂D₁. При таком построении четырехугольник ABCD будет плоским. Пользуясь вспомогательными прямыми, пересекающимися со сторонами четырехугольника, можно построить проекции пятиугольника, шестиугольника и т. д.

Построим проекции правильного шестиугольника, вписанного в окружность, при горизонтальном их расположении (рис, 116, а). Построение начинаем с проведения окружности; затем вписываем в нее правильный шестиугольник А₁В₁C₁D₁E₁F₁.

Фронтальная проекция шестиугольника изобразится прямой горизонтально расположенной линией A₂D₂, точки B₂F₂ и С₂Е₂, принадлежащие этой линии, попарно совпадут.

В практике нередко приходится строить наклонно расположенные многоугольники, и особенно, окружности. Придадим плоскостям шестиугольника и круга наклонное положение, т. е. расположим их во фронтально-проецирующей плоскости т (рис. 116, б). При таком расположении плоскости прямые FB и ЕС шестиугольника и диаметр HG круга останутся фронтально-проецирующими прямыми и спроецируются на плоскость П₁ в истинную величину. Наоборот, прямые ВС, AD и FE спроецируются с искажением, зависящим от величины угла наклона плоскости т. В связи с этим горизонтальная проекция шестиугольника не будет являться правильным шестиугольником, а горизонтальная проекция круга будет проецироваться эллипсом, большая ось которого H₁G₁, малая — A₁D₁

Аналитический портал Ua-News Главные новости Украины: политика, интернет, шоу-BIZ, спорт, столица.

Построение проекций точек, принадлежащих цилиндру и конусу

Пусть задана фронтальная проекция F₂ точки F, принадлежащей боковой поверхности цилиндра вращения (рис. 164, а). Требуется построить три проекции точки F. Как известно, цилиндр вращения образуется путем вращения прямоугольника вокруг одной из его сторон, принимаемой за ось вращения. Противоположная сторона прямоугольника (образующая или производящая) образует при вращении боковую поверхность цилиндра; две другие стороны прямоугольника образуют верхнее и нижнее основания цилиндра, являющиеся кругами одного и того же диаметра.

Поверхность цилиндра является в данном случае горизонтально-проецирующей поверхностью; следовательно, горизонтальная проекция F₁ точки Р должна совпадать с горизонтальной проекцией боковой поверхности цилиндра (с окружностью).

Проекция F₂ изображена светлым кружком; значит, точка F принадлежит передней поверхности цилиндра и спроецируется на нижнюю половину окружности в точку F₁. Третью проекцию F₃ строим с помощью ординаты у, откладывая ее размер вправо от оси z₃.

При построении изометрического изображения удобно пользоваться видимым для нас верхним основанием цилиндра (рис. 164, б). Строим эллипс в плоскости х’О’у’, проводим касательные-к нему прямые— видимые образующие цилиндра — и нижний полуэллипс. Точку F’ находим с помощью координатной ломаной, что ясно из сравнения чертежей.

Пусть требуется построить три проекции точки G, принадлежащей поверхности конуса вращения (рис. 165, а).

Конус вращения образуется при вращении прямоугольного треугольника вокруг одного из его катетов. Гипотенуза прямоугольного треугольника является при этом образующей конуса. Верхняя точка образующей является вершиной конуса. Второй катет треугольника образует при вращении основание конуса. Судя по чертежу, вершина конуса расположена выше основания, поэтому вся боковая поверхность конуса будет видимой при проецировании на горизонтальную плоскость проекций П₁; при проецировании на фронтальную плоскость проекций П₂ видимой будет передняя половина боковой поверхности.

Фронтальная проекция G₂ задана светлым кружком, т. е. точка G принадлежит передней поверхности конуса. Для построения горизонтальной проекции G₁ существуют два способа: способ образующей и способ параллели. Рассмотрим способ образующей. Соединяем фронтальные проекции S₂ и G₂ прямой линией S₂H₂. Это будет фронтальная проекция образующей SH. Находим ее горизонтальную проекцию S₁H₁. Горизонтальную проекцию G_1. искомой точки G находим, проведя вертикальную линию связи G₂G₁. Этот способ не дает точного результата в тех случаях, когда точка лежит вблизи передней образующей конуса. Более универсальным является второй способ — способ параллели. Он заключается в проведении через точку G окружности или параллели а. Ее фронтальная проекция а₂ пересекает фронтальную проекцию левой образующей в точке А₂. Находим точку А₁ и радиусом А₁S₁ из центра S₁ проводим окружность а₁ — горизонтальную проекцию параллели а. Пересечение окружности с вертикальной линией связи определяет точку G₁. Третью проекцию G₃ находим с помощью ординаты у так же, как в предыдущей задаче; изображаем ее зачерненным кружком, поскольку точка G при проецировании на плоскость П₃ невидимая.

Найдите среднюю линию и проекция боковой стороны стороны равносторонней проекции на большую основу , если боковая сторона равняется 17 см , высота – 15см , а меншая основа – 10 см.

Ответ оставил Гуру

Проекция боковой стороны трапеции на большее основание равна Пр = sqrt (17^2 -15^2) = sqrt (17^2 -15^2) = sqrt (64) = 8

Т.к. трапеция равнобокая, то и проекция второй боковой стороны на большее основание равна 8.

Большее основание равно сумме меньшего основания и двух проекций боковых сторон: Б осн = 10+8+8 =26.

Средняя линия трапеции равна полусумме оснований: Ср лин = (10+26)/2 = 18

Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Геометрия.

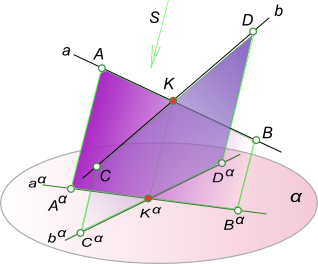
Ортогональное проецирование

Ортогональное проецирование является частным случаем параллельного проецирования, при котором направление проецирования S перпендикулярно плоскости проекции α.

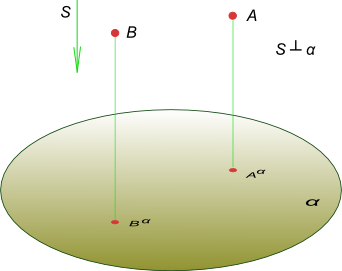
Рисунок дает наглядное представление об ортогональным проецированием точки.

Кроме отмеченных ранее свойств параллельных проекций, для ортогонального проецирования будет справедлива следующая теорема:

для того чтобы прямой угол проецировался ортогонально без искажения, необходимо и достаточно, чтобы, по крайней мере, одна его сторона была параллельна плоскости проекции, а вторая сторона не перпендикулярна к этой плоскости.

Для доказательства этой теоремы обратимся к чертежу

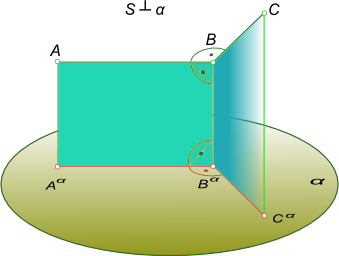
В пространстве ABC = 90°, сторона AB данного угла параллельна плоскости проекции α, а сторона ВС не перпендикулярна этой плоскости, докажем, что A α B α C α = 90°.

Фигура ABB α A α – прямоугольник, следовательно, AB перпендикулярен к проецирующей плоскости BCC α B α , так как он перпендикулярен к двум пересекающимся прямым этой плоскости (AB ⊥ BB α по построению). Но AB║A α B α , Следовательно, A α B α ⊥ плоскости BCC α B α , поэтому A α B α ⊥B α C α , т. е. A α B α C α = 90°.

Ортогональное проецирование обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием. Это: – простота геометрических построений для определения ортогональных проекций точек; – возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. При ортогональном проецировании если проецируемая фигура параллельна плоскости проекций, то ее проекция на данную плоскость не искажена или конгруентна проецируемой фигуре. Отмеченные достоинства обеспечили широкое применение ортогонального проецирования, в частности, для составления машиностроительных чертежей.

Центральное и параллельное (косоугольное) проецирования позволяют однозначно решать задачу по определению проекции фигуры по заданному оригиналу, но не дают возможности воспроизвести (реконструировать) оригинал по его одной центральной или косоугольной проекции. Для того чтобы получить ортогональный чертеж, обладающий свойством “обратимости”, необходимо иметь, по крайней мере, две связанные между собой ортогональные проекции оригинала.

Проекция боковой стороны

Вопрос по геометрии:

Найдите среднюю линию и проекция боковой стороны стороны равносторонней проекции на большую основу , если боковая сторона равняется 17 см , высота – 15см , а меншая основа – 10 см.

Ответы и объяснения 1

Проекция боковой стороны трапеции на большее основание равна Пр = sqrt (17^2 -15^2) = sqrt (17^2 -15^2) = sqrt (64) = 8

Т.к. трапеция равнобокая, то и проекция второй боковой стороны на большее основание равна 8.

Большее основание равно сумме меньшего основания и двух проекций боковых сторон: Б осн = 10+8+8 =26.

Средняя линия трапеции равна полусумме оснований: Ср лин = (10+26)/2 = 18

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат – это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи – смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Свойства параллельного проецирования

Геометрические фигуры проецируются на плоскость проекции, в общем случае, с искажениями. Причем характер искажений проекций по сравнению с оригиналом зависит от аппарата проецирования и положения проецируемой фигуры по отношению к плоскости проекции. В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин). Действительно, пусть дана прямоугольная трапеция ABCD. Плоскость трапеции не параллельна плоскости проекции α. Определим параллельную проекцию при заданном направлении проецирования s.

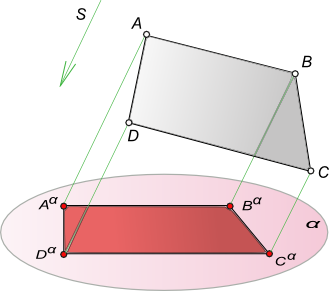
Из рисунка видно, что проекция ABCD Существенно отличается от оригинала ABCD. Изменились длины сторон трапеции, другими стали величины углов при ее вершинах. При таких условиях, естественно, нарушается равенство площадей фигуры оригинала и ее проекции.

Наряду с этим, между оригиналом и его проекцией существует определенная связь, заключающаяся в том, что некоторые свойства оригинала сохраняются и на его проекции. Такие свойства принято называть проективными или инвариантными (независимыми) для данного способа проецирования.

Основу любой геометрии составляет система аксиом. Любые геометрические определения и предложения, равно как и доказательства теорем, базируются на принятой системе аксиом. В процессе параллельного проецирования (получения проекций геометрической фигуры по ее оригиналу) или реконструкции чертежа (воспроизведение оригинала по заданным его проекциям), любое определение, любую теорему можно составить и доказать, опираясь на инвариантные свойства параллельного проецирования, которые играют в начертательной геометрии такую же важную роль, как аксиомы в геометрии.

Таким образом, можно утверждать, что в начертательной геометрии существует, как бы, две системы аксиом: – первая используется в процессе построения проекции геометрической фигуры по ее оригиналу. На этом этапе функции аксиом выполняют инвариантные свойства параллельного проецирования; После того, как проекции определены, можно рассматривать задачу как плоскую, вступает в силу вторая система – аксиоматика евклидовой геометрии.

Основные инвариантные свойства параллельного проецирования:

1. Проекция точки есть точка.

Это очевидно из самого определения проекции как точки пересечения проецирующего луча с плоскостью проекций.

2. Проекция прямой на плоскость есть прямая.

Действительно, при параллельном проецировании все лучи, проецирующие точки A,B,C,D,E прямой l, принадлежат одной плоскости Υ, параллельной направлению проецирования s. Эта плоскость пересекает плоскость проекции по прямой l α . (Исходя из этого справедливо и следующее утверждение. Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций.)

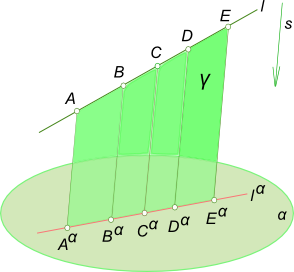
3. Если в пространстве точка принадлежит (инцидентна) линии, то проекция этой точки принадлежит проекции линии. Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.

4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.

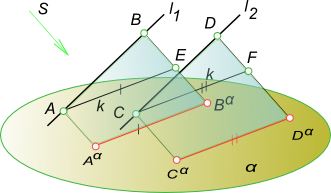
Если [AB]║[CD], то плоскости ABB α A α и CDD α C α параллельны как имеющие углы при вершинах B и D с соответственно параллельными сторонами – (BA)║(DC) и (BB α )║(DD α ). Эти плоскости пересекаются плоскостью проекции α по параллельным прямым l α ₁║l α ₂. Проведем в проецирующей плоскости ABB α A α через точку A прямую k₁║l₁, а в плоскости CDD α C α прямую k₂║l₂. Эти прямые пересекут проецирующие лучи [BB α ) и [DD α ) в точках E и F. Отрезок [AE] [A α B α ], а [CF] [C α F α ] как отрезки параллельных между параллельными. ΔABE подобен ΔCDF. На основании подобия треугольников можно записать:

Из четвертого свойства следует:

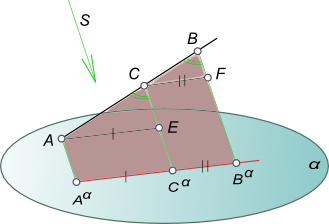
а) если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией этой точки в том же отношении.

Доказательство этого свойства аналогично предыдущему, понятно из чертежа на рисунке и не требует дополнительных пояснений.

Как следствие пункт a) можно записать: середина отрезка оригинала проецируется в середину его проекции. Поэтому медианы треугольника проецируются в медианы его проекций, а следовательно, центр тяжести треугольной пластинки проецируется в центр тяжести треугольника – проекций; центр окружности, как точка, делящая все диаметры пополам, проецируется в центр эллипса. Взаимно перпендикулярные диаметры окружности проецируются в сопряженные диаметры эллипса.

б) Проекции конгруентных отрезков взаимно параллельных прямых взаимно параллельны и конгруэнтны.

Поэтому проекцией любого параллелограмма будет параллелограмм. В параллелограммы проецируется также произвольно расположенный по отношению к плоскости проекции прямоугольник, ромб, квадрат.

5. Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых. Пусть две прямые a и b пересекаются в точке K. Так как точка K принадлежит прямой a, то на основании свойства 3 K α ∈ a α . Одновременно K ∈ b, следовательно, K α ∈ b α . Эти два условия могут быть удовлетворены только в том случае, если K α будет точкой пересечения проекций прямых a и b.

6. Плоская фигура, параллельная плоскости проекции, проецируется на эту плоскость в конгруентную фигуру.

7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.

Следствием этого свойства будут: – плоская ломанная линия проецируется, в общем случае, в ломанную линию с тем же числом вершин; – плоская кривая проецируется, в общем случае, в кривую линию; – проекция в виде отрезка прямой не определяет оригинала, которым могут быть: прямая, плоская ломанная или кривая линии, любая плоская фигура.

8. Параллельный перенос оригинала или плоскости проекции не изменяет вида и размеров проекции оригинала.

Найдите среднюю линию и проекция боковой стороны стороны равносторонней проекции на большую основу , если боковая сторона равняется 17 см , высота — 15см , а меншая основа — 10 см.

Проекция боковой стороны трапеции на большее основание равна Пр = sqrt (17^2 -15^2) = sqrt (17^2 -15^2) = sqrt (64) = 8

Т.к. трапеция равнобокая, то и проекция второй боковой стороны на большее основание равна 8.

Большее основание равно сумме меньшего основания и двух проекций боковых сторон: Б осн = 10+8+8 =26.

Средняя линия трапеции равна полусумме оснований: Ср лин = (10+26)/2 = 18

как понимать: проекция боковой стороны равнобедренной трапеции на основание?

Равнобедренная трапеция Свойства и признаки равнобедренной трапеции

1. Углы при основании равнобедренной трапеции равны.

2. Диагонали равнобедренной трапеции равны.

3. Если углы при основании трапеции равны, то она равнобедренная.

4. Если диагонали трапеции равны, то она равнобедренная.

5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.

как понимать: проекция боковой стороны равнобедренной трапеции на основание?

Равнобедренная трапеция Свойства и признаки равнобедренной трапеции

1. Углы при основании равнобедренной трапеции равны.

2. Диагонали равнобедренной трапеции равны.

3. Если углы при основании трапеции равны, то она равнобедренная.

4. Если диагонали трапеции равны, то она равнобедренная.

5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.

Чему равна проекция боковой стороны равнобедренного треугольника на его основание? Ответ поясните.

Проекция боковой стороны на его основание равна квадратному корню отношения основания на его боковую сторону

Если ответ по предмету Геометрия отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.

как понимать: проекция боковой стороны равнобедренной трапеции на основание?

Равнобедренная трапеция Свойства и признаки равнобедренной трапеции

1. Углы при основании равнобедренной трапеции равны.

2. Диагонали равнобедренной трапеции равны.

3. Если углы при основании трапеции равны, то она равнобедренная.

4. Если диагонали трапеции равны, то она равнобедренная.

5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.