Найти проекцию треугольника

Проекции точки и прямой, принадлежащих плоскости общего положения

Одной из задач, для решения которых применяются линии уровня, является задача на построение проекций точки, принадлежащей плоскости. Пусть имеется фронтальная проекция D₂ точки D принадлежащей плоскости, заданной следами k X l (рис. 111, а). Требуется найти горизонтальную проекцию D₁ точки D.

Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей плоскости. Решаем задачу с помощью горизонтали h плоскости k X l. Через точку D₂ проводим фронтальную проекцию h₂ этой горизонтали, которая, как известно, должна быть параллельна оси х₁₂ (Рис. 111 б). Она пересечет фронтальную проекцию k₂ фронтального следа k к точке N₂; проведя вертикальную линию связи, найдем на оси проекций х₁₂ горизонтальную проекцию фронтального следа N горизонтали (см. рис. 108).

Горизонтальная проекция h₁ горизонтали должна быть параллельна l₁, Горизонтальную проекцию D₁ точки D найдем на горизонтальной проекции h₁ горизонтали в точке пересечения ее с вертикальной линией связи, проведенной через точку D₂.

Эту задачу можно было бы решить также с помощью фронтали. В этом случае пришлось бы через точку D₂ провести фронтальную проекцию f₂||k₂. Советуем учащимся выполнить построение самим. Результат должен быть одинаковым с первым построением.

Несколько изменим условия задачи. Пусть будет задана горизонтальная проекция Е₁ точки Е и плоскость ABC, определенная проекциями треугольника (рис, 112, а), В этой задаче нельзя воспользоваться горизонталью плоскости, поскольку отсутствует фронтальная проекция точки Е. Применяем фронталь f; через точку E₁ проводим горизонтальную проекцию (х фронтали, находим ее фронтальную проекцию l2 и на ней точку Е₁.

Точку в плоскости можно построить не только с помощью горизонтали и фронтали, но и с помощью прямой общего положения. В некоторых случаях это даже удобнее.

программа передач на сегодня: Animal Planet, Bloomberg, 3 канал, CNN, Ajara TV, Classic Sport, Amazing Life, AB Moteurs Luxe HD, Jetix, , Jetix Play, Mezzo, HD Кино, Discovery Channel, MCM, MGM, HD Life, Discovery Science.

Определение натуральной величины отрезка

Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Метод прямоугольного треугольника

Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник AA’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A равен величине Z_A – Z_B, то есть разности удаления точек A и B от горизонтальной плоскости П₁.

Откладываем A’A = Z_A – Z_B перпендикулярно A’B’. Затем проводим гипотенузу AB’ треугольника AA’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.

Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E’F’ не изменится, когда она займет новое положение E’₁F’₁ (как это показано на рисунке ниже).

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’₁F’₁ = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E”₁ и F”₁. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.

Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.

Поворот вокруг оси

Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’₁N’₁, параллельное оси X.

По линиям связи находим точку M”₁. При этом исходим из того, что M” в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N”₁ и M”₁ искомым отрезком. На рисунке он выделен красным цветом.

Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.

Geogebra – бесплатное он-лайн геометрическое приложение

Geogebra – наилучшее он-лайн геометрическое приложение для рисования геометрических фигур.
Подождите. Идёт загрузка (прим. 1-2 минуты).
Открыть в полный экран

Открыть в полный экран
Это он-лайн приложение позволяет рисовать геометрические фигуры – точки, линии, углы, треугольники, многоугольники, круги.
Вы можете создавать анимиционную геометрию и слайды.
Если Вам не нужна система координат по умолчанию, Вы можете скрыть ее.

Проекции треугольника, многоугольника и круга

Итак, найдя постоянную прямую чертежа, мы можем построить одну из возможных систем плоскостей проекций. Очевидно, что начало координат любой системы должно находиться на постоянной прямой чертежа. Отсюда следует, что постоянная прямая чертежа является геометрическим местом точек, фиксирующих начало координат всех возможных систем плоскостей проекций П₂, П₃.

При построении проекций четырехугольника общего положения нельзя взять четыре произвольные точки. Как только мы возьмем три точки, плоскость определится, и четвертую точку надо строить при условии, чтобы она принадлежала этой плоскости. Практически пользуются диагоналями проекций четырехугольника (рис. 115, в).

Фронтальную проекцию четырехугольника ABCD Рис. 116 строим произвольно; также произвольно строим горизонтальные проекции трех точек А₁, В₁ и С₁ треугольника A₁B₁C₁. Для построения горизонтальной проекции D₁ точки D проводим фронтальные проекции А₂С₂ и D₂B₂ диагоналей четырехугольника.

Проекции диагоналей пересекутся между собой в точке Е₂. Находим горизонтальную проекцию E₂ этой точки на горизонтальной проекции А₁С₁ будущей диагонали АС; соединяем точки В₁ и E₁ и на продолжении этой линии находим точку D₁ на вертикальной линии связи D₂D₁. При таком построении четырехугольник ABCD будет плоским. Пользуясь вспомогательными прямыми, пересекающимися со сторонами четырехугольника, можно построить проекции пятиугольника, шестиугольника и т. д.

Построим проекции правильного шестиугольника, вписанного в окружность, при горизонтальном их расположении (рис, 116, а). Построение начинаем с проведения окружности; затем вписываем в нее правильный шестиугольник А₁В₁C₁D₁E₁F₁.

Фронтальная проекция шестиугольника изобразится прямой горизонтально расположенной линией A₂D₂, точки B₂F₂ и С₂Е₂, принадлежащие этой линии, попарно совпадут.

В практике нередко приходится строить наклонно расположенные многоугольники, и особенно, окружности. Придадим плоскостям шестиугольника и круга наклонное положение, т. е. расположим их во фронтально-проецирующей плоскости т (рис. 116, б). При таком расположении плоскости прямые FB и ЕС шестиугольника и диаметр HG круга останутся фронтально-проецирующими прямыми и спроецируются на плоскость П₁ в истинную величину. Наоборот, прямые ВС, AD и FE спроецируются с искажением, зависящим от величины угла наклона плоскости т. В связи с этим горизонтальная проекция шестиугольника не будет являться правильным шестиугольником, а горизонтальная проекция круга будет проецироваться эллипсом, большая ось которого H₁G₁, малая — A₁D₁

Аналитический портал Ua-News Главные новости Украины: политика, интернет, шоу-BIZ, спорт, столица.

Найти проекцию треугольника

Практикум по решению задач.

По координатам трех точек А(45,30,10), B(30,10,45) и С(5,25,5) построить проекции плоскости и её следы.

В плоскости треугольника АВС провести горизонталь, фронталь и линию наибольшего ската.

Построить недостающую проекцию плоскости заданной двумя пересекающимися прямыми a и b , если известно, что она является профильно проецирующей плоскостью.

Построить следы плоскости заданной двумя параллельными прямыми.

Изменить способ задания плоскости на эпюре (от следов перейти к двум пересекающимся прямым).

ОСНОВЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ и инженерной графики

Пример 2 (Рис.54). Треугольник (АВС) спроецировать в натуральную величину и в прямую линию. (3 и 4 задачи преобразования).

1) Заданный треугольник спроецируется в прямую линию, если новая плоскость проекций окажется перпендикулярной к плоскости этого треугольника. Или – к какой-либо прямой его плоскости. Практически – роль такого ориентира может играть линия уровня в плоскости треугольника. В данном случае – это горизонталь

, которая на новую плоскость проекций должна спроецироваться в точку. Итак, в пространстве задаем новую плоскость проекций (), на чертеже – (натуральной величине).

2) Строим вырожденную прямую в линию проекцию треугольника:

3) Задаем очередную новую плоскость проекций

, на чертеже – .

4) Строим натуральную величину треугольника:

, так как в системе плоскостей проекций и треугольник находится в плоскости уровня.

Способ вращения вокруг проецирующей прямой

В процессе вращения геометрической фигуры каждая ее точка описывает в пространстве окружность, плоскость которой перпендикулярна к оси вращения, а центр – в точке пересечения оси и этой плоскости (Рис.55). Если ось вращения – проецирующая прямая и, соответственно, плоскость вращения – плоскость уровня, то следует вывод:

Траектория вращения точки на плоскость, перпендикулярную к оси вращения, проецируется без искажения, а на плоскость, параллельную оси, – в виде прямой линии, параллельной оси проекций (Рис.56).

Способ может быть использован для всех 4-х задач преобразования.

Пример (Рис.57). Спроецировать отрезок

в натуральную величину и – в точку. Для первого вращения использовать заданную ось . Для второго вращения ось j задать самостоятельно.

1) Повернуть отрезок

вокруг оси i до положения фронтали

2) Через один из концов отрезка задать ось вращения

и повернуть отрезок в положение горизонтально проецирующей прямой

Способ прямоугольного треугольника

Способ прямоугольного треугольника применяется в задачах, в которых требуется определить натуральную величину отрезка, разность координат концов отрезка, углы наклона его к плоскостям проекций и так далее. Посмотрим на способ прямоугольного треугольника как частный случай замены плоскостей проекций. Это тот случай определения длины отрезка, когда один из его концов принадлежит плоскости проекций, а новая плоскость проекций проводится через сам отрезок (Рис.58). На чертеже это новая ось, совпадающая с проекцией отрезка. При этом искомая величина отрезка окажется равной гипотенузе прямоугольного треугольника, один из катетов которого есть проекция отрезка. Помимо длины треугольник содержит в себе и другие сведения об отрезке.

Точно такой же треугольник с точно такими же сведениями об отрезке можно получить без операции проецирования и даже – на безосном комплексном чертеже. Применим одну из проекций отрезка за катет прямоугольного треугольника. Второй катет равен разности координат концов отрезка в направлении, в каком была задана выбранная проекция. Что имеем в итоге:

1) Длина отрезка равна гипотенузе прямоугольного треугольника, один катет которого – это проекция отрезка, второй катет – равен разности координат концов отрезка, измеренной в направлении получения использованной проекции отрезка.

2) Угол наклона отрезка к плоскости проекций равен углу между гипотенузой и проекцией отрезка на той же плоскости.

Пример (Рис.59). Определить длину отрезка

и угол его наклона к плоскости .

При определении длины отрезка за катет прямоугольного треугольника может быть выбрана любая проекция отрезка. Другое дело, если определяется угол наклона отрезка к той или иной плоскости проекций. Здесь выбор падает на проекцию отрезка, принадлежащую именно той же плоскости проекций.

Строим прямоугольный треугольник, приняв за катет фронтальную проекцию отрезка

. Второй катет по длине равен разности координат точек и в направлении мнимой в данном случае оси y. На чертеже эта разница берется на другой плоскости проекций: на плоскости . Из построенного треугольника делаем выводы:

1)

,

2)

.

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C” и D”, следуя этому свойству, заняли положение C”₁ и D”₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C”₁ и D”₁. Стрелками показано перемещение точек C” и D” параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M”₁N”₁ = M”N” на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M”₂ = N”₂ определяются по линиям связи.

Определение натуральной величины треугольника

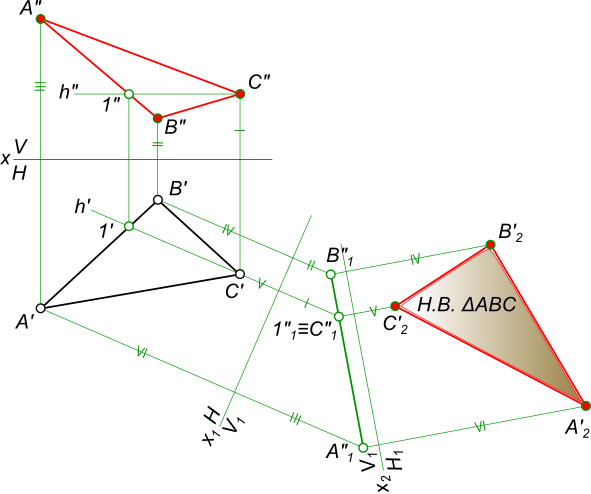
Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A”₁, B”₁, C”₁.
3. Перемещаем проекцию A”₁B”₁C”₁ треугольника ABC в положение A”₂B”₂C”₂, параллельное оси X, соблюдая равенство A”₂B”₂C”₂ = A”₁B”₁C”₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

Натуральная величина треугольника

Натуральная величина треугольника на эпюре Монжа может быть определена: – способом прямоугольного треугольника;

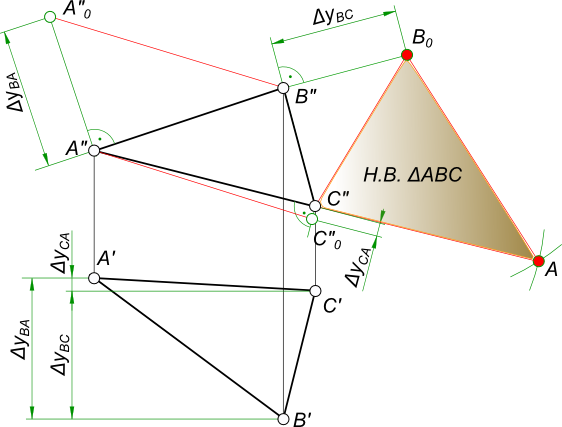
Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.

Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:

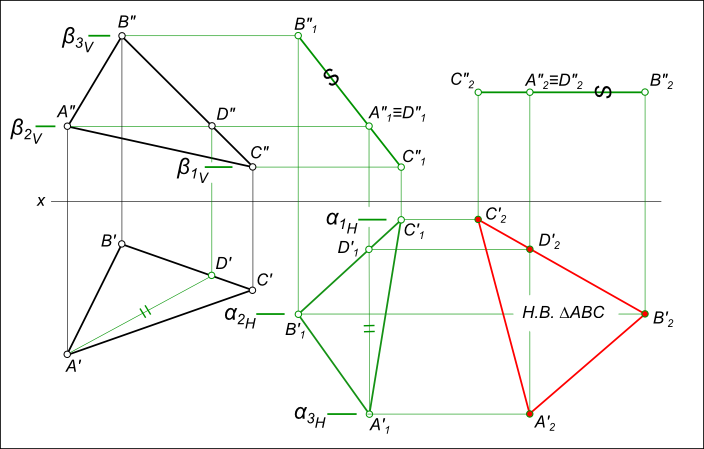
– Способ вращения вокруг осей перпендикулярных плоскостям проекций;

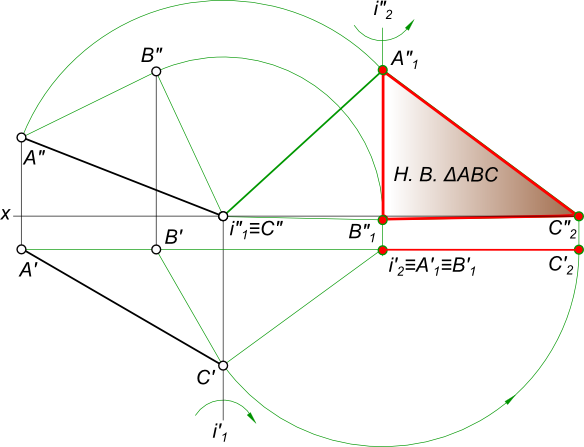
– Вращение вокруг горизонтали представляющих собой линии уровня;

представляющих собой линии уровня;

– Вращение вокруг следа или способ совмещения с плоскостью проекций;

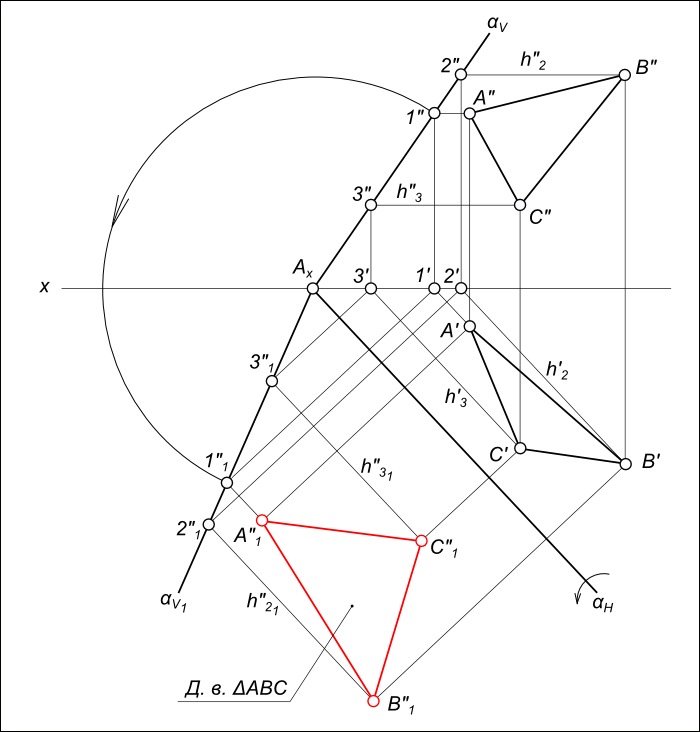
Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.

Проекции прямоугольного треугольника

Построить Проекции прямоугольного треугольника ABC, если его катет AB(A`B`, . ) принадежит горизонтальной прямой h(h`, h”), катеты равны между собой, а вершина C принадлежит прямой m(m`, . ) и zC больше zB

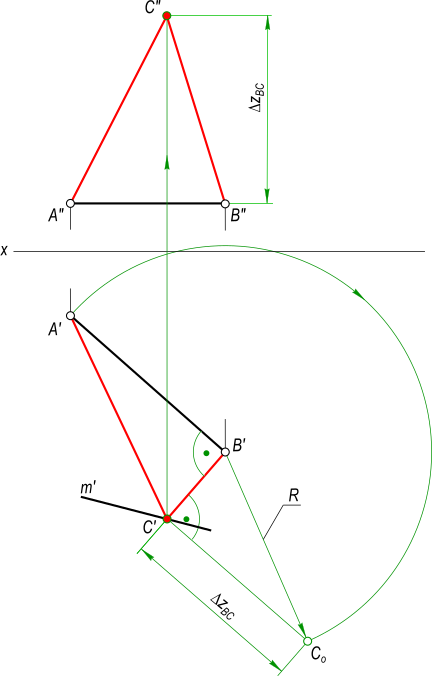
AB – один из катетов прямоугольного треугольника, представляет собой прямую уровня – горизонтальную прямую так как A”B” || Ox. На горизонтальную плоскость проекции он проецируется в натуральную величину. Выполняем построение BC: – прямой угол при вершине B проецируется без искажения на горизонтальную плоскость проекции, следовательно здесь можно провести направление для катета BC; – в пересечении направления катета BC с m` получим C`. По способу прямоугольного треугольника определяем Δz = zC-zB: – из центра O описываем дугу радиусом R=|AB|=A`B` до пересечения с направлением перпендикуляра в точке C0; – определяем разницу аппликат катета BC – Δz. Откладываем Δz на фронтальной плоскости проекций от точки B” и по линии проекционной связи находим точку C”.

Построить проекции прямоугольного равнобедренного треугольника ABC, катет которого BC лежит на прямой MN. A(60,40,10), M(75,10,30); N(15,25,30).

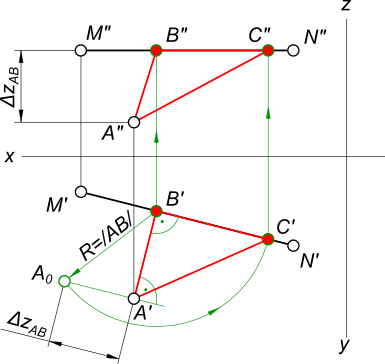
Так как zM=zN делаем вывод, что отрезок MN – горизонтальная прямая и мы можем опустить из точки A перпендикуляр на него. В пересечении которого с M`N` находим B` и затем по линии проекционной связи B”. Находим натуральную величину катета AB способом прямоугольного треугольника:
– через точку A проводим перпендикуляр к AB и на нем откладываем ΔzAB и находим A0 и BA0; – откладываем на отрезке MN катет BC, описывая дугу радиуса R=/AB/ и отмечая точку C` и по линии проекционной связи C”; – вершины A`B`C` и A”B”C” соединяем прямыми линиями, получая проекции искомого треугольника.

Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
Построить фронтальную и горизонтальную проекции параллелограмма ABCD

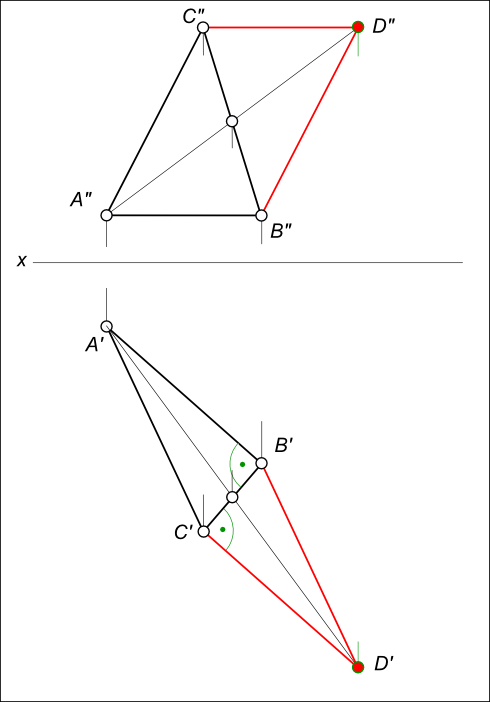
Построение параллелограмма заключается: – в проведении BD // AC; – в проведении CD // AB.

Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
Построить фронтальную и горизонтальную проекции квадрата ABCD

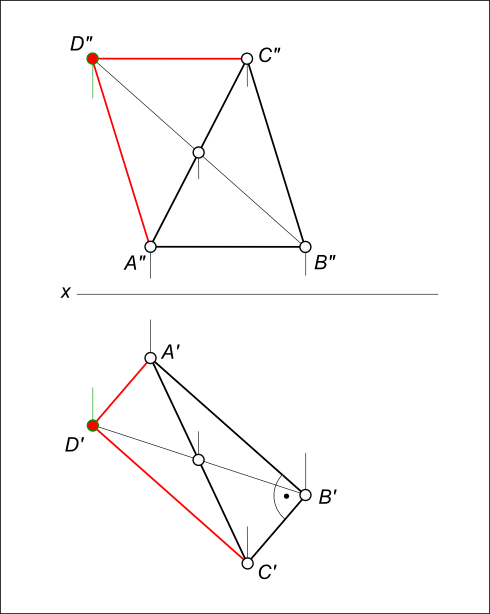
Построение квадрата заключается: – в проведении AD // BC; – в проведении CD // AB.

Найти проекцию треугольника

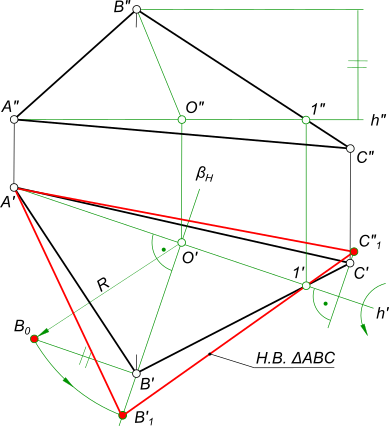
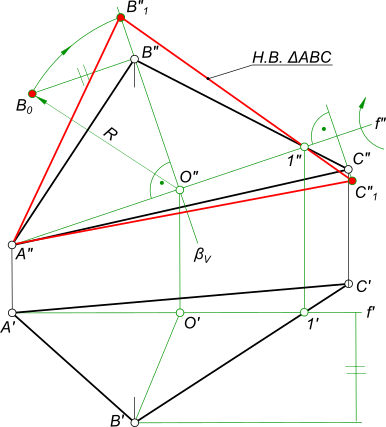
Вращением вокруг оси, параллельной плоскости проекций, найти натуральную величину треугольника АВС.

Определим натуральную величину треугольника вращением вокруг горизонтали:

В плоскости треугольника проведем горизонталь h₂ и найдем её горизонтальную проекцию h₁;

Определим методом прямоугольного треугольника радиусы этих окружностей R_A=O₁ A A₁ 1 , R_B=O₁ B B₁ 1 ;

Отложив полученные радиусы на горизонтальных проекциях окружностей – траекторий вращения точек А и В, получим искомую проекцию натуральной величины треугольника А₁ 2 В₁ 2 С₁.

Проекции катетов на гипотенузу

Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.

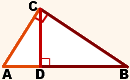
Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.

1) Свойство высоты, проведенной к гипотенузе.

Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.

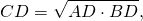
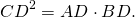
2) Свойства катетов прямоугольного треугольника.

Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.

Проекции треугольника

Проекции треугольника,одного и того же, представлены в трех вариантах:

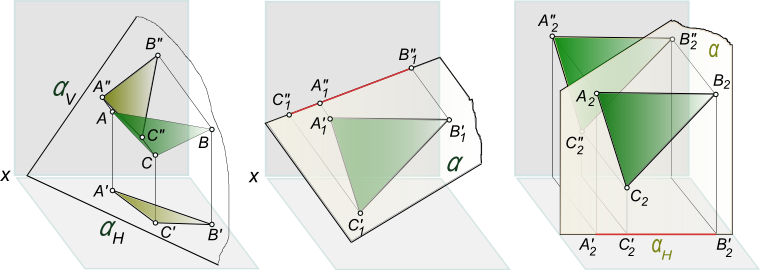
1. вариант – ΔABC, занимает общее положение; 2. вариант – ΔA₁B₁C₁ ⊥ V, занимает положение перпендикулярное к фронталной плоскости проекций; 2. вариант – ΔA₂B₂C₂ ║ V, занимает положение параллельное относительно фронталной плоскости проекций; ΔABC≅ΔA₁B₁C₁≅ΔA₂B₂C₂

Данные проекции треугольника показывают, что вид проекции (ее форма и размеры) определяются не только формой и размерами проецируемой фигуры, но и в значительной степени зависит от взаимного расположения объекта проецирования и плоскости проекций.

Действительно, три конгруентных прямоугольных треугольника ΔABC≅ΔA₁B₁C₁≅ΔA₂B₂C₂ (рисунок) в зависимости от взаимного расположения плоскости треугольника и плоскости проекции V могут проецироваться на эту плоскость в виде: а) ΔA”B”C” соответствует ΔABC, плоскость треугольника занимает произвольное положение относительно плоскости V. ΔA”B”C” в метрическом отношении не имеет ничего общего с оригиналом – ΔABC (рисунок слева); б) отрезка прямой [C”₁B”₁], в случае, когда плоскость ΔA₁B₁C₁⊥V (рисунок в центре) перпендикулярна к фронталной плоскости проекций; в) либо в виде ΔA”₂B”₂C”₂ ≅ ΔA₂B₂C₂, когда плоскость ΔA₂B₂C₂ ║ V (рисунок справа) параллельна относительно фронталной плоскости проекций.

Сопоставляя между собой оригинал – треугольник ABC и проекции треугольника в различных положениях, мы видим, что только в случае параллельности проецируемой фигуры плоскости проекции возможно получить проекцию на эту плоскость, конгруентную самой фигуре, и, следовательно, полностью сохраняющую ее метрику. Форма и размеры фронтальной проекции ΔA”₂B”₂C”₂ (рисунок справа) позволяют, без каких либо построений, ответить на вопросы: какова длина сторон треугольника, величина углов при вершинах, чему равна его площадь и другие метрические характеристики ΔA₂B₂C₂.

Решение задачи по определению натуральной величины треугольника ΔABC показано в статьях: Графическая работа 3; Натуральная величина треугольника.

Онлайн калькулятор. Проекция вектора на другой вектор.

Этот онлайн калькулятор позволит вам очень просто найти проекцию одного вектора на другой вектор.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление проекции вектора на вектор и закрепить пройденый материал.

Калькулятор для вычисления проекции вектора на другой вектор

Инструкция использования калькулятора для вычисления проекции вектора на другой вектор

Ввод даных в калькулятор для вычесления проекции вектора на другой вектор

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления проекции вектора на другой вектор

• Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

Теория. Проекция вектора на вектор

Определение Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b. Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:

Пр b a =	a · b
| b |

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Примеры решения задач. Задача 1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника)

Задача 1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника).

Дано: Решение:

Строим прямоугольный треугольник, взяв за один катет горизонтальную (или фронтальную) проекцию отрезка – проекцию А₁В₁ (рис.4.3), а за другой – разность удалений концов отрезка от горизонтальной плоскости проекций Dz=z_В-z_А (или соответственно от фронтальной плоскости проекций – Dy=y_В-y_А). Величину Dz можно определить, проведя вспомогательную линию через один из концов отрезка перпендикулярно линии связи. Гипотенуза прямоугольного треугольного треугольника А₁В₁В_о и будет равна истинной величине отрезка АВ. Угол между гипотенузой и катетом, равным горизонтальной проекции отрезка, определяет величину угла наклона j заданного отрезка к горизонтальной плоскости проекций. Для определения угла наклона y к фронтальной плоскости проекций необходимо еще раз построить истинную величину отрезка с помощью прямоугольного треугольника А₂АВ₂. При этом |АА₂|=|А₁В|. Если по условию задачи требуется определить только истинную величину отрезка прямой, достаточно построить прямоугольник на одной из проекций.

Задача 2. Разделить отрезок АВ точкой С в отношении 2:3 (рис.4.4).

Для того, чтобы построить точку С, делящую отрезок в заданном отношении, достаточно одну из проекций отрезка (на рис. 4.4) горизонтальная проекция) разделить в этом отношении, а затем построить вторую проекцию искомой точки, используя линию связи. Деление проекции А₁В₁ произведено с помощью теоремы Фалеса. Для этого из любого конца проекции А₁В₁, например из точки А₁ проводим луч под произвольным углом, на котором откладываем 2+3=5 равных отрезков произвольной длины. Соединяем точки ВВ₁, затем проводим через С прямую СС₁||BB₁.

Задача 3. Достроить отрезок АВ, если длина его равна 50 мм (рис.4.5).

Задача является обратной к определению истинной величины отрезка прямой.

Дано: Решение:

Для того, чтобы достроить фронтальную проекцию точки A(A₂) необходимо знать разность удалений концов отрезка АВ от плоскости p₁: Dz=z_В-z_А, значение которой можно узнать, построив прямоугольной треугольник, взяв за один из катетов известную горизонтальную проекцию отрезка АВ. Треугольник построен по известному катету и гипотенузе (известной истинной величине отрезка АВ). Из прямоугольного треугольника А₁В₁В находим, что Dz=|В₁В|. Задача имеет два решения (две точки A₂ и A’₂).

Задача 4. На прямой a (a₁,a₂) от точки А отложить отрезок АС, длиной 30 мм (рис.34.6).

На прямой а зададимся произвольным отрезком АВ. С помощью прямоугольного треугольника А₁В₁В определим истинную величину отрезка АВ. Далее от точки А₁ откладываем вдоль гипотенузы заданный отрезок 30 мм. Определяем искомую точку С(С₁,С₂), используя положение о пропорциональности деления отрезка, при этом СС₁||ВВ₁.

Задача 5. (Задача на профильные прямые). Достроить прямую NM, параллельную прямой КL (рис.4.7).

Замечание. Задачи на профильные прямые могут быть решены различными методами, в частности, с помощью построения третьей проекции этих прямых, либо с помощью методов косоугольного параллельного проецирования путем построения, так называемых, вспомогательных прямых. К этому типу задач следует отнести задача по определению взаимного положения профильных прямых, построения точки пересечения профильных прямых, а также ряд позиционных задач, связанных с построением точек пересечения профильной прямой и плоскости. Приведем решение задачи на профильные прямые методом построения вспомогательных прямых.

Дано: Решение:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8661 –

| 7436 – или читать все.