Чему равна проекция силы на ось

Термех взаимодействия и движения материальных тел

Решение задач на равновесие сходящихся сил с помощью построения замкнутых силовых многоугольников в большинстве случаев сопряжено с громоздкими построениями. Более общим и универсальным методом решения таких задач является переход к определению проекций заданных сил на координатные оси и оперирование с этими проекциями. Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.

Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (—), если направление от начала проекции к ее концу противоположно положительному направлению оси.

Рассмотрим ряд случаев проецирования сил на ось:

1. Вектор силы (рис. 12, а) составляет с положительным направлением оси х острый угол . Чтобы найти проекцию, из начала конца вектора силы опускаем перпендикуляры на ось х; получаем

Проекция вектора в данном случае положительна.

2. Сила (рис. 12, б) составляет с положительным направлением оси x тупой угол . Тогда , но так как

Проекция вектора в данном случае отрицательна.

3. Сила (рис. 12, в) перпендикулярна оси х. Проекция силы F на ось х равна нулю

Итак, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.

Силу, расположенную на плоскости хОу (рис. 13), можно спроектировать на две координатные оси Ох и Оу. На рисунке изображена сила и ее проекции Fx и Fy, Ввиду того что проекции образуют между собой прямой угол, из прямоугольного треугольника АСВ следует:

Этими формулами можно пользоваться для определения модуля и направления силы, когда известны ее проекции на координатные оси.

Кинематикой называется раздел теоретической механики, в котором изучаются геометрические свойства механического движение тел, без учета их масс и действующих на них сил.

Под механическим движением понимается изменение с течением времени положение тела в пространстве по отношению к другим телам. Для того чтобы определить изменение положения тела по отношению к другому телу, с последним связывают какую-либо систему координатных осей, называемую системой отсчета. В зависимости от тела, с которым она связана, система отсчета может быть как подвижной, так и неподвижной. Тело движется по отношению к выбранной системой отсчета, если с течением времени изменяются координаты хотя бы одной из его точек; в противном случае тело по отношению к данной системе отсчета будет находиться в состоянии покоя. Таким образом, покой и движение – понятия относительные, зависящие от выбора системы отсчета.

Механическое движение происходит в пространстве и во времени. При этом пространство считается трехмерным евклидовым пространством. Все измерения в нем производятся на основании методов евклидовой геометрии. За единицу длины при измерении расстояния принят 1 метр. Время в механике считается универсальным, т.е. протекающем одинаково во всех системах отсчета. За единицу времени принимается 1 секунда.

Теоретический материал, модули 1-4

Загрузить всю книгу

Титульный лист

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Тольяттинский государственный университет

Кафедра теоретической механики

ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ

для студентов, обучающихся по образовательной технологии «30/70»

Составил: к.ф.-м.н., доцент Прасолов С. Г.

к.т.н., доцент Будаев С. И.

Научный редактор: ст. преп. Шадрина С.П.

Утверждено научно-методическим советом университета.

© Тольяттинский государственный университет, 2005

Чему равна проекция силы на ось

Тема 3 . Сложение сил на плоскости

Система сил , линии действия которых лежат в одной плоскости называется плоской.

Геометрический способ сложения сил. Геометрическая сумма (главный вектор) системы сил F₁, F₂, . F_n определяется построением силового многоугольника. Для этого пользуются правилом сложения векторов. В произвольной точке О вектор R , соединяющий начало первого вектора F₁ с концом последнего F_n изображает геометрическую сумму или главный вектор слагаемых сил:

R = F₁ + F₂ + . + F_n = S F_k. (k = 1, 2, . n)

Проекцией силы на ось называется алгебраическая величина , равная произведению модуля силы на косинус угла между силой и положительным направлением оси:

F_х = | F |Ч cos a.

Аналитический способ задания сил на плоскости

Силу F на плоскости Оxy можно задать через ее проекции F_хи F_уна оси прямоугольной системы координат по правилу сложения векторов, определив точку А ( x_A , y_A ) приложения силы:

F = F_хЧ i + F_уЧ j,

где i, j – единичные векторы. Модуль силы F и углы, которые она образует с координатными осями вычисляются по формулам:

cos (F, i) = F_х /F, cos (F, j) = F_y /F.

Аналитический способ сложения сил

Воспользуемся теоремой: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Спроецируем равенство R = S F_k на оси прямоугольной системы координат Оху , получим

Rх = S Fkx , Ry = S Fky , (k = 1, 2, . n)

где F_kx, F_ky – проекции k-ой силы F_k на оси Ох и Оу соответственно. Тогда на плоскости Оху вектор R равные геометрической сумме слагаемых сил F₁, F₂, . F_n определяется по формулам:

R = R_хЧ i + R_уЧ j;

Лекции и примеры решения задач по теормеху, сопромату, ТММ и ДМ

Проекция силы на ось – это алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на соответствующие оси. Рисунок 1.13):

Проекция силы на ось может быть положительной, рис. 1.13а ( 0 ≤ α β = π/2) и отрицательной, рис. 1.13в ( π/2 P_z = P ∙ sinα;
P_x = (P ∙ cosα)cosβ;
P_y = (P ∙ cosα)cosγ = P ∙ cosα ∙ cos(90 o — β).

Лекции и примеры решения задач по теормеху, сопромату, ТММ и ДМ

Момент силы относительно оси, например O_z (рисунок 1.18), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси ( F’) относительно точки пересечения оси с плоскостью, т.е.

Момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.

Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например M_z(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, M_z(Q).

Момент силы относительно оси – скалярная величина.

Моменты силы относительно координатных осей можно получить, расписав векторное произведение

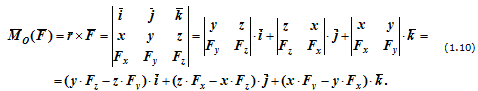
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.

Проекция силы на ось. Проекция векторной суммы сил на ось

Решение задач на равновесие сходящихся сил с помощью построения замкнутых силовых многоугольников сопряжено с громоздкими построениями. Универсальным методом решения таких задач является переход к определению проекций заданных сил на координатные оси и оперирование с этими проекциями. Осью называют прямую линию, которой приписано определенное направление.

Проекция вектора на ось является скалярной величиной, которая опреде­ляется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.

Проекция вектора считается положительной, если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной, если направление от начала проекции к ее концу противоположно положительному направлению оси.

Таким образом, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.

Рассмотрим ряд случаев проецирования сил на ось.

Вектор силы F (рис. 2.2) составляет с положительным напра­влением оси х острый угол

.

Чтобы найти проекцию, из начала и конца вектора силы опускаем перпендикуляры на ось oх; получаем

Проекция вектора в данном случае положительна

Сила F (рис. 2.3) составляет с положительным направлением оси х тупой угол α.

Тогда F_x = F cos α, но так как α = 180 0 – φ,

Проекция силы F на ось oх в данном случае отрицательна.

Сила F (рис. 2.4) перпендикулярна оси oх.

Проекция силы F на ось х равна нулю

Силу, расположенную на плоскости хоу (рис. 2.5), можно спроектировать на две координатные оси ох и оу.

Силу F можно разложить на составляющие: F_x и F_y. Модуль вектора F_x равен проекции вектора F на ось ox, а модуль вектора F_y равен проекции вектора F на ось oy.

Модуль силы

можно найти по теореме Пифагора:

.

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Проекция силы на ось

Часто геометрическое сложение векторов сил требует сложных и громоздких построений. В таких случаях прибегают к другому методу, где геометрическое построе­ние заменено вычислениями скалярных величин. Дости­гается это проектированием заданных сил на оси прямо­угольной системы координат.

Как известнее из математики, осью называют неограни­ченную прямую линию, которой приписано определенное направление. Проекция вектора на ось является скаляр­ной величиной, которая определяется отрезком оси, отсе­каемым перпендикулярами, опущенными из начала и конца вектора на ось.

Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (—), если направление от на­чала проекции к ее концу противоположно положитель­ному направлению оси.

Рассмотрим ряд случаев проектирования сил на ось.

1. Дана сила Р (рис.а), она лежит в одной пло­скости с осью х. Вектор силы составляет с положительным направлением оси острый уголα.

Чтобы найти величину проекции, из начала и конца вектора силы опускаем перпендикуляры на ось х, полу­чаем

Р_х = ab = Р cos α.

Проекция вектора в данном случае положительна.

2. Дана сила Q (рис. б), которая лежит в одной плоскости с осью х, но ее вектор составляет с положи­тельным направлением оси тупой угол α.

Проекция силы Q на ось х

Q_х = ab = Q cos α,

cos a = — cos β.

Так как α > 90°, то cos cos α — отрицательная величина. Выразив cos α через cos β (β — острый угол), оконча­тельно получим

В этом случае проекция силы отрицательна.

Итак, проекция силы на ось координат равна произве­дению модуля силы на косинус угла между вектором силы и положительным направлением оси.

При определении проекции вектора силы на ось поль­зуются обычно косинусом острого угла, независимо от того, с каким направлением оси — положительным или отрицательным — он образо­ван. Знак проекции легче устанавливать непосредствен­но по чертежу.

Силу, расположенную на плоскости хОу, можно спроек­тировать на две координатные оси Ох и Оу. Рассмотрим рисунок.

На нем изображена сила Р и ее проекции Р_х и Р_у. Ввиду того что проекции образуют между собой прямой угол, из прямоугольного треугольника ABC следует:

Этими формулами можно пользоваться для определения величины и направления силы, когда из­вестны ее проекции на координатные оси. Эти же формулы могут применяться для определения величины и направ­ления любого вектора через его проекции.

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Проекция векторной суммы на ось. Теорема о проекции векторной суммы

Заданы сходящиеся силы

(рис. а).

Геометрическая сумма, или равнодействую­щая, этих сил

определяется замыкающей стороной

силового многоугольника (рис. б).

Спроектируем все вершины силового многоугольника ABCDEKL на ось х и обозначим их проекции соответ­ственно а, b, с, d, е, k, l.

Проекции сил на ось х изобра­зятся отрезками:

Сумму проекций можно представить в следующем виде:

Так как al есть проекция равнодействующей силы

на ось х, т.е. al = R_x , то

где n — число слагаемых векторов.

Следовательно, проекция векторной суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

В плоскости геометрическую сумму сил можно спроек­тировать на две координатные оси, а в пространстве соответственно на три.

Проекция силы на ось и на плоскость

Перейдем к рассмо­трению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус – если в отрицательном. Из определения следует, что проек­ции данной силы на любые параллельные и одинаково направлен­ные оси равны друг другу. Этим удобно пользоваться при вычисле­нии проекции силы на ось, не лежащую в одной плоскости с силой.

Рис. 12

Обозначать проекцию силы

на ось Ох будем символом . Тогда для сил, изображенных на рис. 12, получим:

, .

Но из чертежа видно, что

, .

, ,

т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным на­правлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси – острый, и отрицательной, если этот угол – тупой; если сила перпен­дикулярна к оси, то ее проекция на ось равна нулю.

Рис.13

Проекцией силы

на плоскость Оху называется вектор , заключенный между проекциями начала и конца силы на эту плоскость (рис. 13). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим чис­ленным значением, но и направлением в плоскости Оху. По модулю , где — угол между направ­лением силы и ее проекции .

В некоторых случаях для нахож­дения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось ле­жит, а затем найденную проекцию на плоскость спроектировать на данную ось. Например, в случае, изображенном на рис. 13, найдем таким способом, что

Равновесие системы сходящихся сил.

Из законов меха­ники следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инер­ции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.

Отсюда получаем два важных вывода: 1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции». 2) Уравно­вешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравнове­шенных сил.

Для равновесия приложенной к твердому телу системы сходя­щихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовле­творять сами силы, можно выразить в геометрической или аналити­ческой форме.

1. Геометрическое условие равновесия. Так как равнодействующая

сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой,т. е. когда много­угольник замкнется.

Следовательно, для равновесия системы, сходящихся сил необ­ходимо и достаточно, чтобы силовой многоугольник, построен­ный из этих сил, был замкнут.

2. Аналитические условия равновесия. Аналитически равнодействующая системы сходящихся сил определяется формулой

.

Так как под корнем стоит сумма положительных слагаемых, то R обратится в нуль только тогда, когда одновременно

, , , т. е. когда действующие на тело силы будут удовлетворять равенствам:

Равенства выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия

Равенства выражают также необходимые условия (или уравнения) равновесия свободного твердого тела, находящегося под действием сходящихся сил.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9239 –

| 7356 – или читать все.

185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Тема 1.2. Статика. Проекции силы на ось

Практическое занятие №1. Плоская система сходящихся сил

Знать способы сложения двух сил и разложение силы на со­ставляющие, геометрический и аналитический способы определе­ния равнодействующей силы, условия равновесия плоской сходящей­ся системы сил.

Уметь определять равнодействующую системы сил, решать задачи на равновесие геометрическим и аналитическим способом, рационально выбирая координатные оси.

Расчетные формулы

Равнодействующая системы сил

где F_∑x, F_∑y — проекции равнодействующей на оси координат; F_kx, F_ky — проекции векторов-сил системы на оси координат.

где — угол равнодействующей с осью Ох.

Если плоская система сходящихся сил находится в равновесии, мно­гоугольник сил должен быть замкнут.

Пример 1. Определение равнодействующей системы сил.

Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П1.1). Дано:

Решение

1. Определить равнодействующую аналитическим способом (рис. П1.1a).

2. Определить равнодействующую графическим способом.

С помощью транспортира в масштабе 2 мм = 1 кН строим много­угольник сил (рис. П1.1б). Измерением определяем модуль равно­действующей силы и угол наклона ее к оси Ох.

Результаты расчетов не должны отличаться более чем на 5%:

Расчетно-графическая работа №1. Определение равнодействующей плоской системы схо­дящихся сил аналитическим и геометрическим способами

Задание 1. Используя схему рис. П1.1а, определить равнодей­ствующую системы сил геометрическим способом

Пример 2. Решение задачи на равновесие аналитиче­ским способом.

Грузы подвешены на стержнях и канатах и находятся в равно­весии. Определить реакции стержней АВ и СВ (рис. П1.2).

Решение

1. Определяем вероятные направления реакций (рис. П1.2а). Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.

Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.

2. Освобождаем точку В от связи (рис. П1.26).

3. Выберем направление осей координат, ось Ох совпадает с ре­акцией R₁.

4. Запишем уравнения равновесия точки В:

5. Из второго уравнения получаем:

Из первого уравнения получаем:

Вывод:стержень АВ растянут силой 28,07 кН, стержень СВ сжат силой 27,87 кН.

Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.

В данном случае реакции направлены верно.

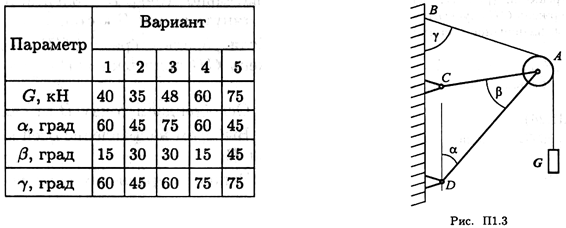Задание 2. Определить реакции стержней АС и AD (рис. П1.3) в аналитической форме.

При защите работ ответить на вопросы карт с тестовыми заданиями.

Темы 1.1, 1.2. Статика. Плоская сходящаяся система сил

Задание для самостоятельной работы 1.

Определить величину и направление реакций связей по данным одного из вариантов, показанных на рисунке.

Задача 1

Задача 2. Определить реакции стержней, удерживающих грузы F₁ и F₂. Массой стержней пренебречь. Схему своего варианта см. на рисунке. Числовые данные своего варианта взять из таблицы.

ЛЕКЦИЯ 4

Тема 1.3. Пара сил и момент силы относительно точки

Знать обозначение, модуль и определение моментов пары сил или относительно точки, условия равновесия системы пар сил.

Уметь определять моменты пар сил и момент силы относительно точки, определять момент результирующей пары сил.

Пара сил, момент пары сил

Парой сил называется система двух сил, равных по модулю, параллельных и направ­ленных в разные стороны.

Рассмотрим систему сил (F, F 1 ), образую­щих пару.

1. Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом.
2. Силы, входящие в пару, не уравновешива­ются, т. к. они приложены к двум точкам (рис. 4.1). Их действие на тело не может быть заменено одной силой (равнодействую­щей).
3. Момент пары сил численно равен произ­ведению модуля силы на расстояние между линиями действия сил (плечо пары).
4. Момент считают положительным, ес­ли пара вращает тело по часовой стрелке (рис. 4.1 б): M(F; F’)= Fa; М > 0.
5. Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.

Свойства пар (без доказательств):

1. Пару сил можно перемещать в плоскости ее действия.
2. Эквивалентность пар. Две пары, моменты которых равны, (рис. 4.2) эквивалентны (действие их на тело аналогично).
3. Сложение пар сил. Систему пар сил можно заменить равно­действующей парой.

Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему (рис. 4.3):

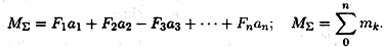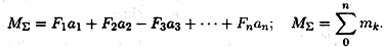4. Равновесие пар.

Для равновесия пар необходимо и достаточно, чтобы алгебраи­ческая сумма моментов пар системы равнялась нулю:

Последнее изменение этой страницы: 2016-04-08; Нарушение авторского права страницы

Лекции и примеры решения задач по теормеху, сопромату, ТММ и ДМ

Для характеристики вращательного действия силы на тело, закрепленное на оси, служит момент силы относительно оси – алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью (рисунок 1.3).

Правило знаков

Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:

где F_П – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Oz с плоскостью П, h — плечо силы.

Момент силы относительно оси обладает следующими свойствами:

1. момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;
2. момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.

Другими словами, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

Проекция силы на ось и на плоскость.

Лекция 2. Равновесие системы сил. Пара сил.

В данной лекции рассматриваются следующие вопросы

1. Проекция силы на ось и на плоскость.

2. Геометрический способ сложения сил.

3. Равновесие системы сходящихся сил.

4. Момент силы относительно центра или точки.

5. Теорема Вариньона о моменте равнодействующей.

10. Теорема о параллельном переносе силы.

11. Приведение плоской системы сил к данному центру.

12. Условия равновесия произвольной плоской системы сил.

13. Случай параллельных сил.

14. Равновесие плоской системы параллельных сил.

15. Сложение параллельных сил. Центр параллельных сил.

16. Понятие о распределенной нагрузке.

17. Расчет составных систем. Статически определимые и статически неопределимые задачи.

18. Графическое определение опорных реакций.

19. Решение задач.

Изучение этих вопросов необходимо в дальнейшем для изучения центра тяжести, произвольной пространственной системы сил, сил трения скольжения, моментов трения качения, решения задач в дисциплине «Сопротивление материалов».

Проекция силы на ось и на плоскость.

Перейдем к рассмо­трению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус – если в отрицательном. Из определения следует, что проек­ции данной силы на любые параллельные и одинаково направлен­ные оси равны друг другу. Этим удобно пользоваться при вычисле­нии проекции силы на ось, не лежащую в одной плоскости с силой.

Рис. 1

Обозначать проекцию силы

на ось Ох будем символом F_x. Тогда для сил, изображенных на рис.1, получим:

Но из чертежа видно, что

т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным на­правлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси – острый, и отрицательной, если этот угол – тупой; если сила перпен­дикулярна к оси, то ее проекция на ось равна нулю.

Рис.2

Проекцией силы

на плоскость Оху называется вектор , заключенный между проекциями начала и конца силы на эту плоскость (рис. 2). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим чис­ленным значением, но и направлением в плоскости Оху. По модулю , где — угол между направ­лением силы и ее проекции .

В некоторых случаях для нахож­дения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось ле­жит, а затем найденную проекцию на плоскость спроектировать на данную ось.

Например, в случае, изображенном на рис. 2, найдем таким способом, что

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9825 –

| 7406 – или читать все.

185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно