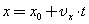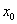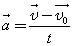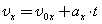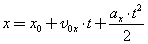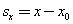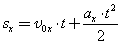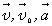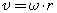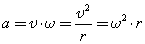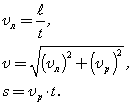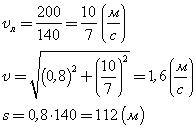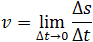Проекция начальной скорости на ось

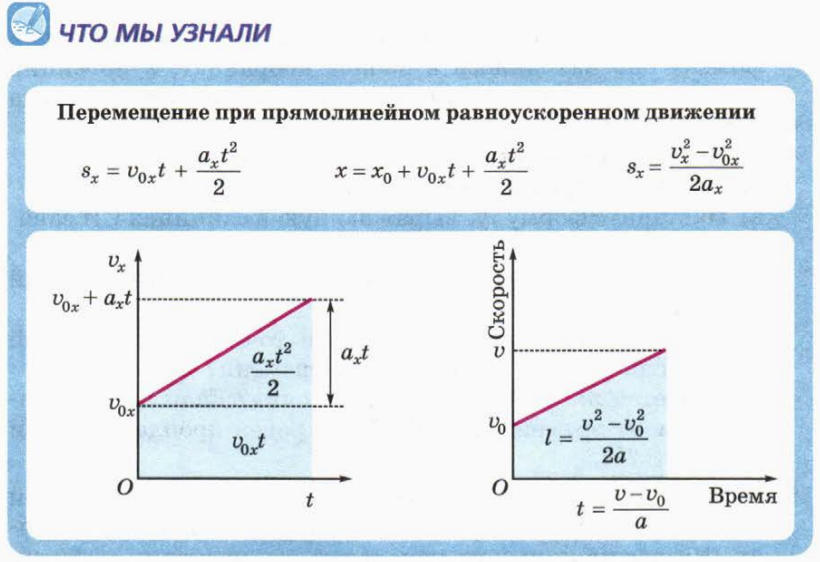
Перемещении при прямолинейном равноускоренном движении

1. Нахождение пути по графику зависимости скорости от времени

Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.

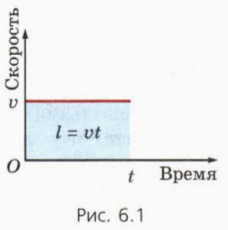
Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.

Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении

путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.

Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.

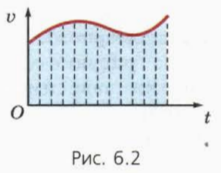
Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.

Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).

Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)

2. Путь и перемещение при прямолинейном равноускоренном движении

Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.

Начальная скорость тела равна нулю

Направим ось x в сторону ускорения тела. Тогда a_x = a, v_x = v. Следовательно,

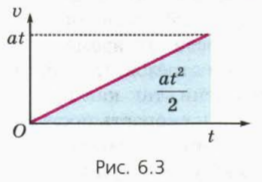
На рисунке 6.3 изображен график зависимости v(t).

? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.

Этим равноускоренное движение существенно отличается от равномерного.

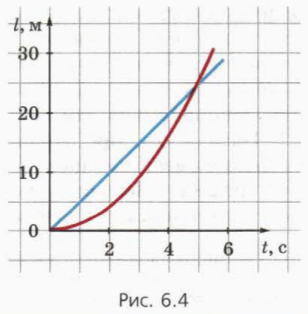
На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.

? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?

? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?

Найдем теперь зависимость проекции перемещения s_x от времени. В данном случае проекция ускорения на ось x положительна, поэтому s_x = l, a_x = a. Таким образом, из формулы (2) следует:

Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда s_x

Начальная скорость тела не равна нулю

Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой

где v_0x – проекция начальной скорости на ось x.

Мы рассмотрим далее случай, когда v_0x > 0, a_x > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).

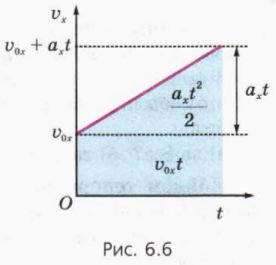
На рисунке 6.6 изображен график зависимости v_x(t) при v_0x > 0, a_x > 0.

? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения

Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения s_x соотношением

где x — начальная координата тела. Следовательно,

Из формул (5), (6) получаем:

6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t 2 .
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.

3. Соотношение между путем и скоростью

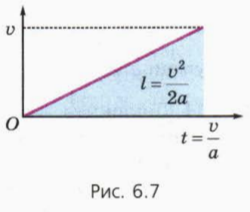
При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:

Подставим это выражение в формулу (2) для пути:

l = at 2 /2 = a/2(v/a) 2 = v 2 /2a. (9)

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.

? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?

Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).

Это соображение поможет вам легко справиться со следующим заданием.

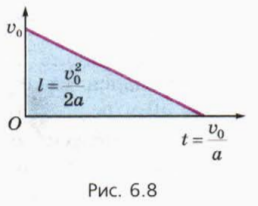
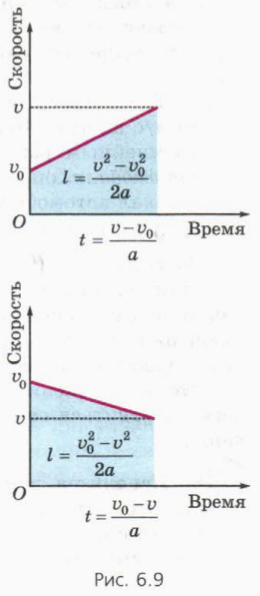
? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь l_т = v 2 /2a, где v – начальная скорость тела, a – модуль ускорения.

В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v и путь, пройденный при разгоне с места до скорости v с тем же по модулю ускорением a, одинаковы.

? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с 2 . Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с 2 . Сравните найденные вами значения тормозного пути с длиной классной комнаты.

? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v 2 – v 2 )/2a, если скорость тела увеличивается;
б) l = (v 2 – v 2 )/2a, если скорость тела уменьшается.

? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением

? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?

Дополнительные вопросы и задания

13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?

14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?

15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости v_x(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?

16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t₁ и t₂ после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t₁ и t₂ составьте систему двух уравнений с двумя неизвестными v и a.
в) Решив эту систему уравнений, выразите v и a через b, t₁ и t₂.
г) Выразите весь пройденный шариком путь l через b, t₁ и t₂.
д) Найдите числовые значения v, a и l при b = 30 см, t₁ = 1с, t₂ = 2 с.
е) Постройте графики зависимости v_x(t), s_x(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.

§ 6. Скорость прямолинейного равноускоренного движения. График скорости

Вам известно, что при прямолинейном равноускоренном движении проекцию вектора ускорения на ось X можно найти по формуле:

Выразим из этой формулы проекцию v_x вектора скорости v, которую имело движущееся тело к концу промежутка времени t, отсчитываемого от момента начала наблюдения, т. е. от t = 0:

Если в начальный момент тело покоилось, т. е. v = 0, то для этого случая последняя формула принимает вид:

Представим зависимость проекции вектора скорости от времени при равноускоренном движении в виде графика.

Из курса математики вам известна линейная функция у = kx + b, где х — аргумент, k — постоянный коэффициент, b — свободный член. Графиком этой функции является прямая.

Функция v_x = v_0x + a_xt (или, что то же самое, v_x = a_xt + v_0x) тоже линейная с аргументом t, постоянным коэффициентом а_х и свободным членом v_0x. Значит, графиком этой функции тоже должна быть прямая. Расположение этой линии по отношению к осям координат определяется значениями а_х и v_0x.

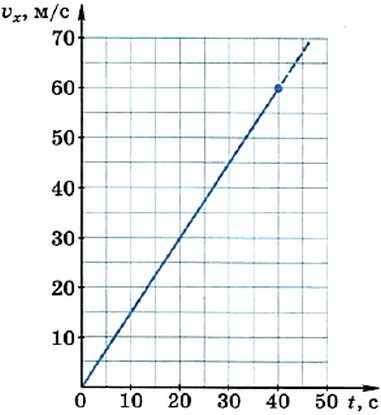
Построим, например, график зависимости от времени проекции вектора скорости разгоняющегося перед взлётом самолёта, который движется из состояния покоя прямолинейно с ускорением 1,5 м/с 2 в течение 40 с.

Сонаправим ось X со скоростью движения самолёта. Тогда проекции векторов скорости и ускорения будут положительны.

Для построения заданной прямой достаточно знать координаты (т. е. t и v_x) двух любых её точек. Задав два произвольных значения t, по формуле v_x = a_xt можно определить соответствующие значения v_x. Например, при t = 0 vx = 0; при t = 40 с v_x = 1,5 м/с 2 • 40 с = 60 м/с. По координатам первой из найденных точек видно, что график зависимости скорости от времени пройдёт через начало координат (рис. 10).

Рис. 10. График функции v_x = 1,5t(м/с)

Теперь построим аналогичный график для случая, когда начальная скорость не равна нулю (при том, что модуль скорости, как и в предыдущем примере, возрастает). Для этого воспользуемся таким примером.

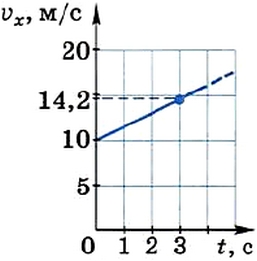
По дороге едет автомобиль со скоростью 10 м/с (36 км/ч). Водитель автомобиля, увидев дорожный знак, снимающий ограничение скорости, нажал на педаль газа, в результате чего автомобиль стал двигаться с постоянным ускорением 1,4 м/с 2 . Построим график зависимости от времени проекции вектора мгновенной скорости на ось X, сонаправленную со скоростью прямолинейно движущегося автомобиля, для первых четырёх секунд разгона.

В этом случае зависимость v_x (t) описывается формулой v_x = v_0x + a_xt. Найдём по этой формуле координаты двух произвольных точек графика. Например, при t = 0 v_0x = 10 м/с; при t = 3 с v_x = 10 м/с + 1,4 м/с 2 • 3 с = 14,2 м/с.

График, построенный по этим точкам, представлен на рисунке 11. Он отсекает на оси v_x отрезок, равный проекции вектора начальной скорости.

Рис. 11. График функции v_x = 10 + 1,4t(м/с)

Построим теперь график зависимости проекции вектора скорости от времени, если начальная скорость не равна нулю, а модуль вектора скорости уменьшается с течением времени.

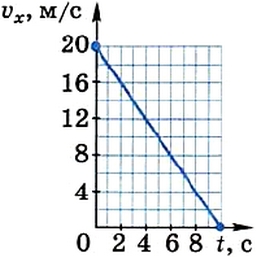
Допустим, водитель автомобиля, движущегося со скоростью 20 м/с (72 км/ч), нажимает на педаль тормоза. В результате автомобиль движется с ускорением 2 м/с 2 и через 10 с останавливается.

За начало отсчёта времени примем момент начала торможения, когда скорость автомобиля ещё была равна 20 м/с.

В этом случае нет необходимости рассчитывать значение проекции вектора скорости, поскольку координаты двух точек графика очевидны: при t = 0 v_0x = 20 м/с; при t = 10 с v_x = 0. Соответствующий график представлен на рисунке 12.

Рис. 12. График функции v_x = 20 – 2t(м/с)

Поскольку скорость уменьшается по модулю, то график образует с положительным направлением оси t тупой угол.

1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.
2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю; б) не равной нулю?
3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках 11 и 12?

Упражнение 6

1. Хоккеист слегка ударил клюшкой по шайбе, придав ей скорость 2 м/с. Чему будет равна скорость шайбы через 4 с после удара, если в результате трения о лёд она движется с ускорением 0,25 м/с 2 ?
2. Лыжник съезжает с горы из состояния покоя с ускорением, равным 0,2 м/с 2 . Через какой промежуток времени его скорость возрастёт до 2 м/с?
3. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось X, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: a) v_0x = 1 м/с, а_х = 0,5 м/с 2 ; б) v_0x = 1 м/с, а_х = 1 м/с 2 ; в) v_0x = 2 м/с, а_х = 1 м/с 2 .

Масштаб: 1 см — 1 м/с; 1 см — 1с.

В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось X, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: a) v_0x = 4,5 м/с, а_х = -1,5 м/с 2 ; б) v_0x = 3 м/с, а_х = -1 м/с 2 .

На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямолинейном движении двух тел. С каким по модулю ускорением движется тело I; тело II?

Проекция начальной скорости на ось

Материалы к зачету по теме “Основные законы механики “

1. Механическое движение.
Явление механического движения тел (материальных точек)состоит в том, что положение тела относительно других тел, т. е. его координаты, с течением времени изменяется.Чтобы найти координаты тела в любой момент времени, нужно знать начальные координаты и вектор перемещения тела. Изменение координаты тела равно проекции вектора перемещения на соответствующую ось координат.

Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:

,

где

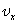— начальная координата тела, а — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.

Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.

Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется.

2. Основная задача механики
состоит в нахождении положения тела в любой момент времени. Решение этой задачи идет по своеобразной «цепочке»:
чтобы найти координату точки, нужно знать ее перемещение, а чтобы вычислить перемещение, нужно знать скорость движения.
По такой цепочке: скорость → перемещение → координата решают задачи механики для прямолинейного равномерного движения.

Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
При прямолинейном ускоренном движении мгновенная скорость тела (материальной точки) непрерывно изменяется от одного момента времени к другому. Поэтому для вычисления скорости в любой момент времени и в любой точке нужно знать быстроту ее изменения, т.е. ускорение:

.

Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле:

.

Координату тела находят по формуле:

.

Проекцию перемещения находят по формуле:

.

Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0.

Значение проекции перемещения при равноускоренном движении можно определить также по формуле:

.

Так как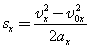

, то для координаты тела х имеем: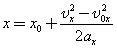

При вычислениях по приведенным формулам знаки проекций векторов

, а также знак начальной координаты х, определяются условием задачи и направлением оси координат.

3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса &#966, проведенного из центра окружности к телу, и угловой скорости ω.

Связь между линейной и угловой скоростью выражается формулой:

,

где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:

.

Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.

Пример решения задачи:

1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.

Вычисления:

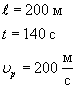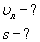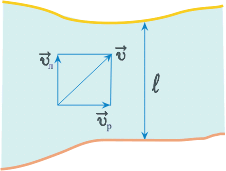Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.

Решите задачи самостоятельно:

1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?

2. 9 км/ч = . м/с; 10 м/с = . км/ч; 8 км/с = . км/ч, 54 км/ч = . м/с.

3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.

Проекция начальной скорости на ось

Получите бесплатный курс по основам математики. Эти знания необходимы для решения задач по физике.

Векторная алгебра с нуля!

Получите бесплатный курс по Векторной алгебре. Он необходим для решения задач по физике.

Книги по изучению физики и для подготовки к ЕГЭ

Проекция вектора. Координатные оси. Проекция точки. Координаты точки на ось

Вначале вспомним, что такое координатная ось, проекция точки на ось и координаты точки на оси.

Координатная ось – это прямая, которой придается какое–то направление. Можете считать, что это вектор с бесконечно большим модулем.

Координатная ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.

Проекция точки на ось – это основание перпендикуляра, опущенного из этой точки на данную ось (рис. 8). То есть, проекцией точки на ось является точка.

Координата точки на ось – это число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.

Скалярная проекция вектора на ось – это число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Важно! Обычно вместо выражения скалярная проекция вектора на ось говорят просто – проекция вектора на ось, то есть слово скалярная опускают. Проекция вектора обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектор а, то его проекция обозначается а_x. При проектировании этого же вектора на другую ось, скажем, ось Y , его проекция будет обозначаться а_y (рис. 9).

Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть

Надо помнить: скалярная проекция вектора на ось (или, просто, проекция вектора на ось) – это число (не вектор)! Причем, проекция может быть положительной, если величина х_к больше величины х_н, отрицательной, если величина х_к меньше величины х_н и равной нулю, если х_к равно х_н (рис. 10).

Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.

Из рисунка 11 видно, что а_x = а Cos α

то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то Cos α > 0 и а_x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.

Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу – отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.

При решении задач часто будут использоваться следующие свойства проекций: если

а = b + c +…+ d , то а_x = b_x + c_x +…+ d_x (аналогично на другие оси),

a = mb, то а_x = mb_x (аналогично на другие оси).

Формула а_x = а Cos α будет очень часто встречаться при решении задач, поэтому ее обязательно надо знать. Правило определения проекции надо знать наизусть!

Запомните!

Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.

Еще раз – НАИЗУСТЬ!

Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

© Коллекция подготовительных материалов для успешной сдачи ЕГЭ по физике от Н. Чернова 2012 – 2015 | Контакты: , +79212839427, (81554) 65780

Равнопеременное прямолинейное движение

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с. Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

= ‘

Проекция вектора скорости на ось ОХ: это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

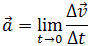
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени: Учитывая, что

– скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:

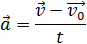
Отсюда формула скорости равнопеременного движения в любой момент времени: Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой: Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

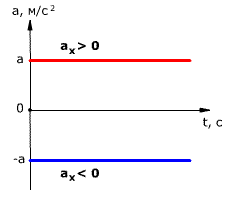
Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

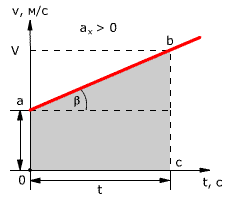
Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

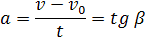
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны: Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

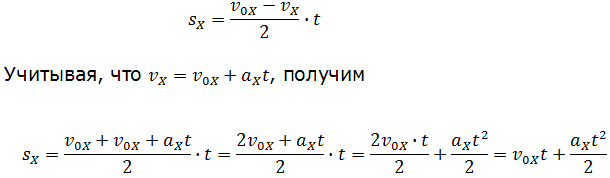
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

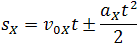
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

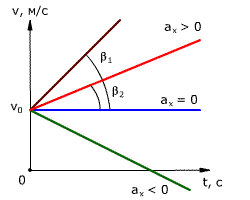
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

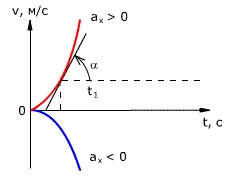
Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

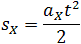
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

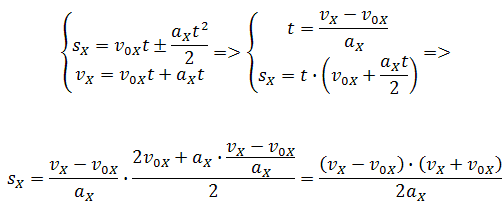
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

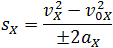
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

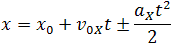
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x

Проекции вектора скорости на оси координат

Скорость – векторная величина, которая определяет быстроту движения и его направление в данный момент времени (измерение в мс).

Кинематика поступательного движения

Средняя скорость

Мгновенная скорость

Модуль мгновенной скорости

Движение в одной плоскости

.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10155 –

| 7772 – или читать все.

185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно