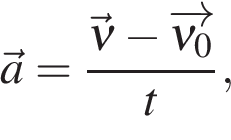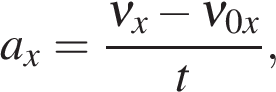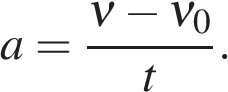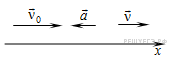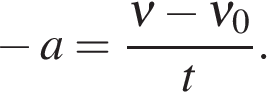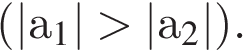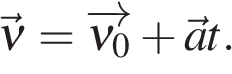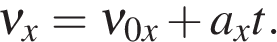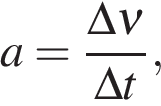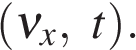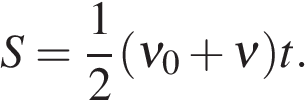Татьяна Ефимова предлагает статью на тему: "найдите проекции скорости тел" с детальным описанием.
Содержание
- 1 1. МЕХАНИКА 1.1. Кинематика
- 2 Скорость прямолинейного равноускоренного движения
- 3 Чему равна проекция скорости тела? (1 июля 2011)
- 4 Найдите проекции скорости тел
- 5 Движение тела, брошенного под углом к горизонту (бросок)
- 6 Прямолинейное равномерное движение
- 7 График проекции скорости в зависимости от времени.
- 8 №22. По заданным графикам (рис. 9) найти начальные координаты тел и проекции скорости их движения. Написать уравнения движения тел х = x(t). Из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками II и III.
- 9 Найдите проекции скорости тел
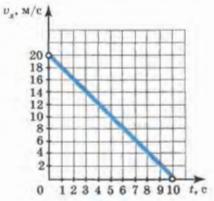
- 10 №61. Проекция скорости движущегося тела изменяется по закону vx= 10 — 2t (величины измерены в СИ).
- 11 Тест № 2. Прямолинейное неравномерное движение
1. МЕХАНИКА
1.1. Кинематика
Движение с ускорением
Равноускоренное прямолинейное движение – движение по прямой с постоянным ускорением (а = const ).
Ускорение а (размерность: м/с 2 ) – векторная физическая величина, показывающая, на сколько изменяется скорость тела за 1 с.
В векторном виде:
В проекции на ось ОХ формула аналогичная
Знаки проекции ускорения зависят от направления вектора ускорения и оси – сонаправлены они или направлены противоположно.
Измерительный прибор – акселерометр. (В ЕГЭ по физике есть вопросы, каким прибором что измеряют.)
График ускорения – зависимость проекции ускорения от времени:
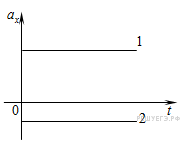
График ускорения при равноускоренном прямолинейном движении – прямая, параллельная оси времени (1, 2).
Чем дальше график от оси времени (2), тем больше модуль ускорения.
Мгновенная скорость – скорость в данный момент времени или в данном месте пространства .
Скорость при равноускоренном прямолинейном движении.
В векторном виде,
в проекции на ось OX,
с учетом знака ускорения («+» разгон, «-» торможение):

График мгновенной скорости – зависимость проекции скорости от времени.
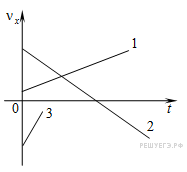
График скорости при равноускоренном прямолинейном движении – прямая (1, 2, 3). Если график располагается над осью времени, то тело движется по направлению оси ОХ.
Чем больше угол наклона графика (3), тем больше модуль ускорения.
Если график пересекает ось времени (2), то на первом этапе тело тормозило, в какой-то момент скорость его стала равной нулю, и далее тело двигалось ускоренно в противоположную сторону.
Геометрический смысл перемещения
|
Все неприличные комментарии будут удаляться. Чему равна проекция скорости тела? (1 июля 2011)Источник: ЕГЭ 2011, О. Ф. Кабардин, С. И. Кабардина, В. А. Орлов. Помогите решить задачу, не сходится ответ, в ответах 0, у меня получается 3, хотя бы по порядку, что и как находим, а решу сам.
КомментарииОдин из вариантов: v = Δx/Δt = x / = (1 + 4t − 2t 2 ) / = 4 − 4t. В уравнение скорости: подставляем t = 1 c. Второй вариант предложите сами.
1) Можно через координаты, построив график зависимости x от t. У нас есть уравнение координаты, значит, xo = 1 м, так как t = 1 c, то подставим в уравнение координаты и получим: x = 1 + 4 × 1 − 2 × 1 × 1 = 3 м, то есть пройденный путь Δx = x − xo, или Δx = 3 − 1 = 2 м. 2) Можно найти путь, пройденный телом, по формуле Δx = vot − (at 2 )/2, или Δx = 4 × 1 − (4 × 1 × 1)/2 = 2 м. Теперь найдём скорость. 1) Можно по формуле Δx = (v 2 − vo 2 ) / (−2a) (минус, так как торможение, что видно из уравнения) или v = √(vo 2 − 2aΔx), то есть v = (4 × 4 − 2 × 4 × 2) = 0 м/c. 2) Можно по формуле Δx = (v + vo)/2, или v = (2Δx − vot)/t, то есть v = (2 × 2 − 4 × 1)/1 = 0 м/с. Найдите проекции скорости тел  
Материалы к зачету по теме “Основные законы механики “1. Механическое движение. Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле: где 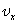 — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи. — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.
Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны. Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется. 2. Основная задача механики Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость. Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле: Координату тела находят по формуле: Проекцию перемещения находят по формуле: Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0. Значение проекции перемещения при равноускоренном движении можно определить также по формуле:
При вычислениях по приведенным формулам знаки проекций векторов 3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω. Связь между линейной и угловой скоростью выражается формулой: где r — радиус окружности. Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения. Пример решения задачи: 1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
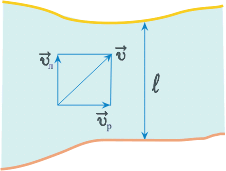
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м. Решите задачи самостоятельно: 1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки 2. 9 км/ч = . м/с; 10 м/с = . км/ч; 8 км/с = . км/ч, 54 км/ч = . м/с. 3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением; Движение тела, брошенного под углом к горизонту (бросок)Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом к оси ОХ (рис. 1). Рис. 1. Тело бросили под углом к горизонту Классическая постановка задач на подобную тематику: тело бросили под углом к горизонту с начальной скоростью , найти различные параметры движения. Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2). Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение) Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( (м/ ), а на ось OY ( (м/ ). Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу. Рис. 3. Тело бросили под углом к горизонту (проекции скоростей) Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим и . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( ), можем найти значения необходимых нам проекций: Вернёмся к рисунку 2. Попробуем найти полное время полёта ( ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения: — т.к. время движения от точки А до B, и от B до C одинаково. Тогда: Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( ). Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время : А с учётом (1) и (5): Перейдём к максимальной высоте полёта ( ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( ) в течение времени , формируем уравнение: Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска. Рис. 4. Тело бросили под углом к горизонту (конечная скорость) Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости: Найдём компоненты вектора . Т.к. движение вдоль оси OX равномерное, значит, , используя (1): Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время , тогда: Используя (5), получим: Подставим (12) и (13) в (10): Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом . Вывод:
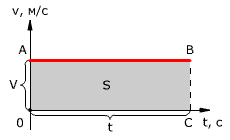
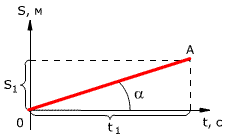
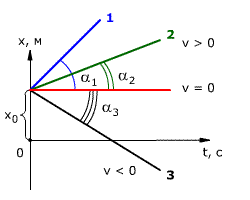
Прямолинейное равномерное движениеРавномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0). Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия. Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени. Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: Проекция перемещения на ось ОХ равна: где x – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени) Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид: Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение. График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна где α – угол наклона графика к оси времени.Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости: Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что следовательно, скорость тела 1 выше скорости тела 2 (v1 > v2). Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть График проекции скорости в зависимости от времени.Равнопеременное движение по прямой. 3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением: 3.1.2. Ускорение ( В векторном виде: где 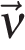 — скорость тела в момент времени t. — скорость тела в момент времени t.
В проекции на ось Ox: где 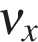 — проекция скорости тела на ось Ox в момент времени t. — проекция скорости тела на ось Ox в момент времени t.
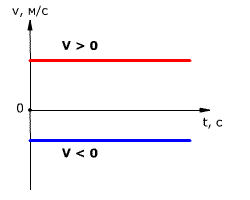
Знаки проекций зависят от направления векторов и оси Ox. График проекции ускорения от времени. При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.): Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения Скорость при равнопеременном движении. В векторном виде: В проекции на ось Ox: Для равноускоренного движения: Для равнозамедленного движения: График проекции скорости в зависимости от времени. График проекции скорости от времени — прямая линия. Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox. Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; 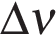 — изменение скорости за время — изменение скорости за время 
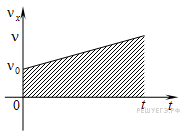
Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение). 3.1.6. Геометрический смысл площади под графиком в осях Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом. На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции: Не нашли то, что искали? Воспользуйтесь поиском: Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 8814 –    185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь. Отключите adBlock! №22. По заданным графикам (рис. 9) найти начальные координаты тел и проекции скорости их движения. Написать уравнения движения тел х = x(t). Из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками II и III.  задача №22 к главе «МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 2. Прямолинейное равномерное движение». 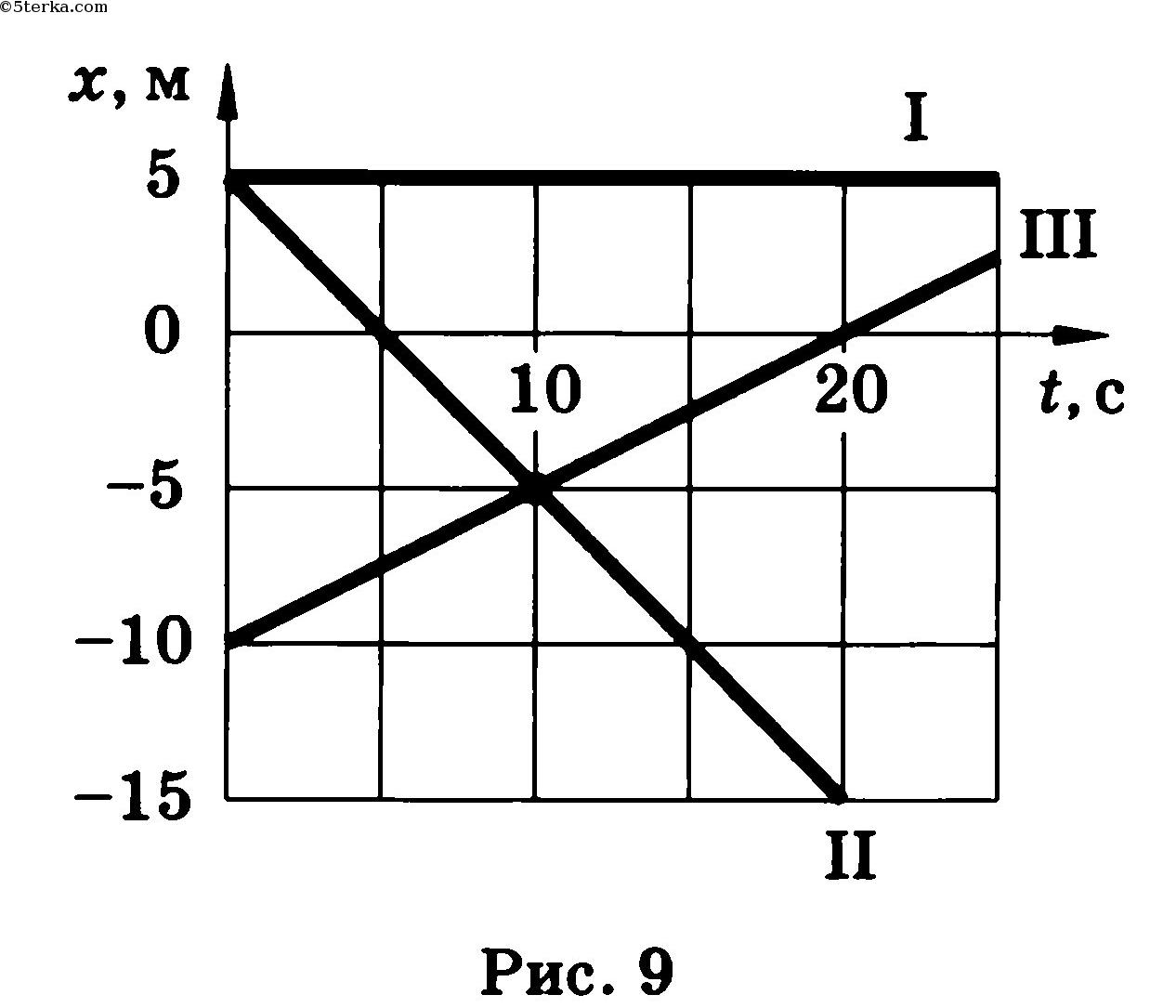 По графику видно, что начальные координаты I тела : 5 м, II: 5 м, III: — 10 м. Скорости движения I: 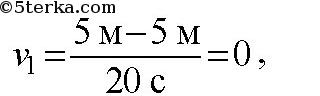 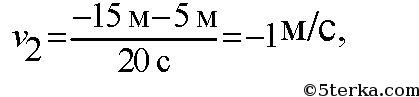 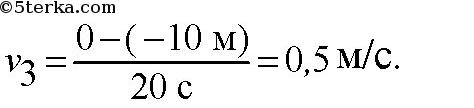 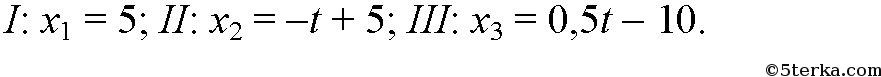 Т.к. движение равномерное вдоль оси Х, то найденные нами скорости v1, v2, v3 являются проекциями на ось Х. По графикам уравнения движения тел II и III видно, что они пересекутся в точке х = – 5 м в момент времени t = 10 с. Найдем это из уравнений движения. Найдите проекции скорости тел«отрицательного ускорения» не бывает. Если движущееся тело снижает скорость-вступает в силу 3-й Закон Ньютона: F/m равно, или больше S/tt. Ньютон пытался уравнять ускорения S/tt и F/m, но ошибка в формуле S=att/2 не позволяла . Ошибку эту он сделал, когда искал ускорение свободного падения «яблока…» Конечная скорость-(9,8…) это НЕ at! at-это СРЕДНЯЯ скорость! Она равна (0+V конечная)/2. Спасибо за альтернативную точку зрения, не указанную в школьных учебниках физики. Надеюсь, это поможет учащимся расширить свой кругозор в области физики. №61. Проекция скорости движущегося тела изменяется по закону vx= 10 — 2t (величины измерены в СИ).  задача №61 к главе «4. Неравномерное прямолинейное движение. Равноускоренное прямолинейное движение тел». №а) Опишите характер движения тела. №б) Найдите проекцию начальной скорости, модуль и направление вектора начальной скорости. №в) Найдите проекцию ускорения, модуль и направление вектора ускорения, Как направлен вектор ускорения по отношению к вектору начальной скорости? №г) Напишите уравнение зависимости проекции ускорения от времени. №д) Постройте графики зависимости vx(t) и ax(t). №е) Найдите графически и аналитически скорости тела через 2 с и 3 с от начала движения. Результат объясните. №ж) Какой физический смысл имеет точка пересечения графика с осью времени? а) движение равноускоренное; в) а = -2 м/с 2 , а и v1 разнонаправлены г) а х = -2 м / с 2 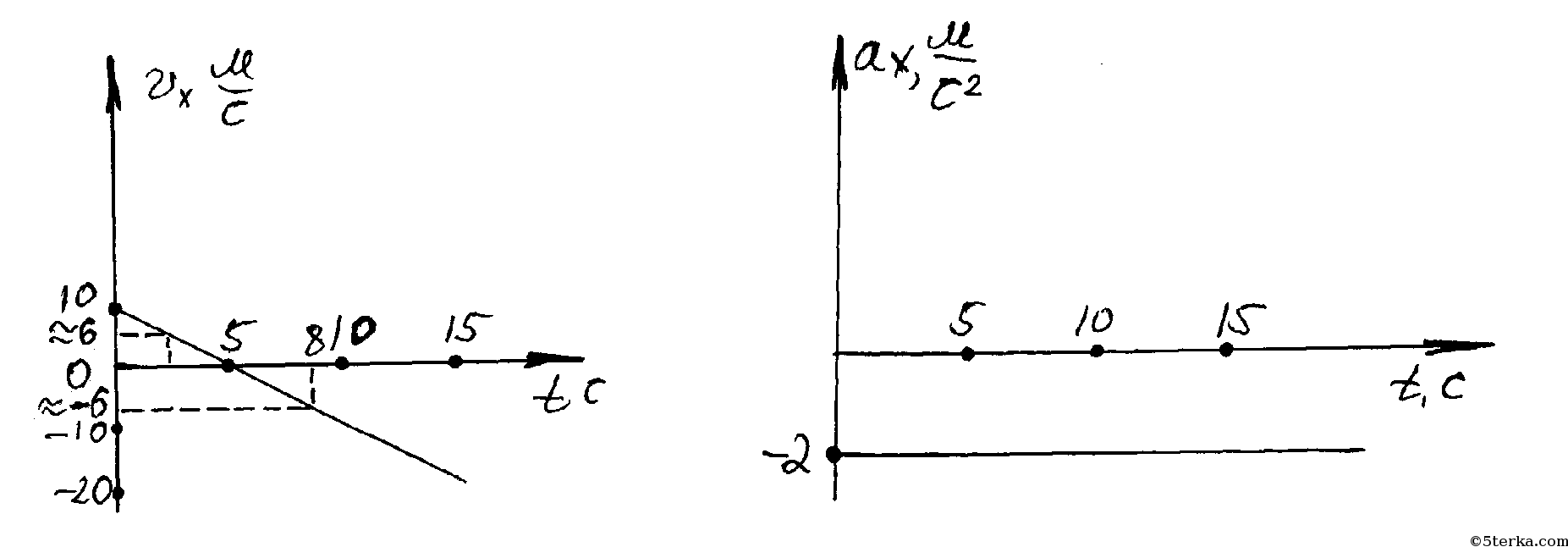 е) v(2) = 10 – 2 ⋅ 2 = 6 м/с v (8) = 10 – 2 ⋅ 8 = -6 м/с модули скорости тела через 2с и 8с совпадают |v| = 6 м/с, а направления скорости различны Тест № 2. Прямолинейное неравномерное движениеВариант 4 1. Ускорением тела при его равноускоренном движении называется величина, равная _____________________________ . a = ___________, s = ___________.  6. По уравнению движения определите начальную координату тела и проекции векторов начальной скорости и ускорения: 7. На рисунке показаны положения двух человек в момент времени t = 0, а также их начальные скорости и ускорения. Запишите уравнения движения.   9. По графику зависимости vx(t) постройте график зависимости ax(t).    10. Сравнитe модули средних скоростей двух тел (поставьте один из знаков: , =).   Не нашли то, что искали? Воспользуйтесь поиском: Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9240 –      185.189.13.12 © xn----ctbetbqubfsc3c1hk.xn--p1ai Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь. Отключите adBlock! Определение проекции скорости По графикам зависимости координаты от времени x ( t ) (или пройденного пути от времени S ( t )) можно рассчитать соответствующую проекцию скорости v x в определенный момент времени (рис. 1.11), например t = t 1 .  Для этого следует: 1) отметить на оси времени указанное значение момента времени t 1 ; 2) восстановить перпендикуляр до пересечения с графиком x ( t ); 3) провести к графику касательную линию в точке его пересечения с перпендикуляром; 4) рассчитать тангенс угла наклона касательной к положительному направлению оси времени; 5) определить проекцию скорости на ось Ox как тангенс угла наклона касательной к положительному направлению оси времени: v x ( t 1 ) = tg α 1 . Следует отметить, что проекция скорости v x является
Пояснение к использованию алгоритма. На рис. 1.12 изображен график зависимости координаты от времени x ( t ). Для определения проекции скорости на ось Ox в момент времени t 3 проведен перпендикуляр t = t 3 . В точке пересечения перпендикуляра с зависимостью x ( t ) проведена касательная линия. Она образует тупой угол с осью t . Следовательно, проекция скорости v x на ось Ox в указанный момент времени является отрицательной величиной: v x ( t 3 ) = − | tg α 3 | .  Определение проекции ускорения По графику зависимости проекции скорости от времени v x ( t ) можно рассчитать проекцию ускорения a x на соответствующую ось в определенный момент времени (рис. 1.13), например t = t 2 . Для этого следует: 1) отметить на оси времени указанное значение момента времени t 2 ; 2) восстановить перпендикуляр до пересечения с графиком v x ( t ); 3) провести к графику касательную линию в точке его пересечения с перпендикуляром; 4) рассчитать тангенс угла наклона касательной к положительному направлению оси времени; 5) определить проекцию ускорения на ось Ox как тангенс угла наклона касательной к положительному направлению оси времени: a x ( t 2 ) = tg α 2 . Следует отметить, что проекция ускорения a x является

 Пояснение к использованию алгоритма. На рис. 1.14 изображен график зависимости проекции скорости от времени v x ( t ). Для определения проекции ускорения на ось Ox в момент времени t 4 проведен перпендикуляр t = t 4 . В точке пересечения перпендикуляра с зависимостью v x ( t ) проведена касательная линия. Она образует тупой угол с осью t . Следовательно, проекция ускорения a x на ось Ox в указанный момент времени является отрицательной величиной: a x ( t 4 ) = − | tg α 4 | . Определение пройденного пути и модуля перемещения (комбинация равномерного и равноускоренного движения) По графику зависимости проекции скорости от времени v x ( t ) можно рассчитать пройденный путь и модуль перемещения материальной точки (тела) за определенный промежуток времени ∆ t = t 2 − t 1 . Для расчета указанных характеристик по графику, содержащему участки только равноускоренного и равномерного движения, следует: 1) отметить на оси времени указанный интервал времени ∆ t ; 2) восстановить перпендикуляры из точек t = t 1 и t = t 2 до пересечения с графиком v x ( t ); 3) рассчитать площадь, ограниченную графиком v x ( t ), перпендикулярами t = t 1 и t = t 2 , осью t ; 4) вычислить пройденный путь S и модуль перемещения ∆ r как суммы: S = S 1 + S 2 + . + S n , ∆ r = S 1 + S 2 + . + S n , где S 1 , S 2 , . S n — пути, пройденные материальной точкой на каждом из участков равноускоренного и равномерного движения. Пояснение к использованию алгоритма . На рис. 1.15 показана зависимость проекции скорости от времени для материальной точки (тела), движущейся на участке AB равноускоренно, на участке BC — равномерно, на участке CD — равноускоренно, но с ускорением, отличающимся от ускорения на участке AB .  В этом случае пройденный путь S и модуль перемещения ∆ r совпадают и рассчитываются по формулам: S = S 1 + S 2 + S 3 , ∆ r = S 1 + S 2 + S 3 , где S 1 — путь, пройденный материальной точкой (телом) на участке AB ; S 2 — путь, пройденный на участке BC ; S 3 — путь, пройденный на участке CD ; S 1 , S 2 , S 3 рассчитываются по алгоритму, приведенному выше. Определение пройденного пути и модуля перемещения (комбинация равномерного, равноускоренного и равнозамедленного движения) Для расчета указанных характеристик по графику v x ( t ), содержащему участки не только равноускоренного и равномерного, но и равнозамедленного движения, следует: 1) отметить на оси времени указанный интервал времени ∆ t ; 2) восстановить перпендикуляры из точек t = t 1 и t = t 2 до пересечения с графиком v x ( t ); 3) рассчитать площадь, ограниченную графиком v x ( t ), перпендикулярами t = t 1 и t = t 2 , осью t ; 4) вычислить пройденный путь S как сумму: S = S 1 + S 2 + . + S n , где S 1 , S 2 , . S n — пути, пройденные материальной точкой на каждом из участков; 5) вычислить модуль перемещения как разность суммарного пути, пройденного материальной точкой до точки остановки, и пути, пройденного материальной точкой после остановки. Пояснение к использованию алгоритма . На рис. 1.16 показана зависимость скорости от времени для материальной точки (тела), движущейся на участке AB равноускоренно, на участке BC — равномерно, на участке CF — равнозамедленно.  В том случае, когда есть участок равнозамедленного движения (включающий точку остановки — точка D ), пройденный путь S и модуль перемещения ∆ r не совпадают. Пройденный путь вычисляют по формуле S = S 1 + S 2 + S 3 + S 4 , где S 1 — путь, пройденный материальной точкой (телом) на участке AB ; S 2 — путь, пройденный на участке BC ; S 3 — путь, пройденный на участке CD ; S 4 — путь, пройденный на участке DF ; S 1 , S 2 , S 3 , S 4 рассчитываются по алгоритму, приведенному выше; необходимо отметить, что величина S 4 является положительной. Модуль перемещения вычисляют по формуле ∆ r = S 1 + S 2 + S 3 − S 4 , вычитая путь, пройденный материальной точкой (телом) после поворота. Определение модуля изменения скорости По графику зависимости проекции ускорения от времени a x ( t ) можно найти модуль изменения скорости ∆ v материальной точки (тела) за определенный интервал времени ∆ t = t 2 − t 1 (рис. 1.17).  Для этого следует: 1) отметить на оси времени указанный интервал времени ∆ t ; 2) восстановить перпендикуляры из точек t = t 1 и t = t 2 до пересечения с графиком a x ( t ); 3) рассчитать площадь, ограниченную графиком a x ( t ), перпендикулярами t = t 1 и t = t 2 , осью t ; 4) вычислить модуль изменения скорости за указанный интервал времени как площадь. Пример 4. График зависимости проекции скорости первого тела на ось Ox от времени изображается прямой, проходящей через точки (0; 6) и (3; 0), второго — через точки (0; 0) и (8; 4), где скорость задана в метрах в секунду, время — в секундах. Во сколько раз отличаются модули ускорений первого и второго тел? Решение. Графики зависимости проекций скорости от времени для обоих тел показаны на рисунке.  Проекция ускорения первого тела определяется как тангенс тупого угла α 1 ; ее модуль вычисляем по формуле | a x 1 | = | tg α 1 | = | tg ( 180 − α 3 ) | = 6 3 = 2 м/с 2 . Первое тело движется равнозамедленно; величина его ускорения составляет a 1 = = 2 м/с 2 . Проекция ускорения второго тела определяется как тангенс острого угла α 2 ; ее модуль вычисляем по формуле a x 2 = tg α 2 = 4 8 = 0,5 м/с 2 . Второе тело движется равноускоренно; величина его ускорения составляет a 2 = 0,5 м/с 2 . Искомое отношение модулей ускорений первого и второго тел равно: a 1 a 2 = 2 0,5 = 4 . Величина ускорения первого тела больше величины ускорения второго тела в 4 раза. Пример 5. График зависимости y -координаты от времени для первого тела изображается прямой, проходящей через точки (0; 0) и (5; 3), второго — через точки (3; 0) и (6; 6), где координата задана в метрах, время — в секундах. Определить отношение модулей проекций скоростей указанных тел. Решение. Графики зависимости y -координаты от времени для обоих тел показаны на рисунке.  Проекция скорости первого тела определяется как тангенс угла α 1 ; ее модуль вычисляем по формуле v y 1 = tg α 1 = 3 5 = 0,6 м/с. Проекция скорости второго тела определяется как тангенс угла α 2 ; ее модуль вычисляем по формуле v y 2 = tg α 2 = 6 3 = 2 м/с. Обе проекции скоростей имеют положительный знак; следовательно, оба тела движутся равноускоренно. Отношение модулей проекций скоростей указанных тел составляет: | v y 2 | | v y 1 | = 2 0,6 ≈ 3 . Величина проекции скорости второго тела больше величины проекции скорости второго тела приблизительно в 3 раза. Пример 6. График зависимости скорости тела от времени изображается прямой, проходящей через точки (0; 4,0) и (2,5; 0), где скорость задана в метрах в секунду, время — в секундах. Во сколько раз путь, пройденный телом, больше модуля перемещения за 6,0 с движения? Решение. График зависимости скорости тела от времени показан на рисунке. Точка остановки τ ост = 2,5 с попадает в интервал от 0 с до 6,0 с.  Следовательно, пройденный путь представляет собой сумму а модуль перемещения — разность | Δ r → | = | S 1 − S 2 | , где S 1 — путь, пройденный телом за интервал времени от 0 с до 2,5 с; S 2 — путь, пройденный телом за интервал времени от 2,5 с до 6,0 с. Значения S 1 и S 2 рассчитаем графически как площади треугольников, показанных на рисунке: S 1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 м; S 2 = 1 2 ⋅ ( 6,0 − 2,5 ) ⋅ 5,6 = 9,8 м. Замечание : значение скорости v = 5,6 м/с в момент времени t = 6,0 c получено из подобия треугольников, т.е. из отношения v 4,0 = 6,0 − 2,5 2,5 − 0 . Вычислим пройденный путь: S = S 1 + S 2 = 5,0 + 9,8 = 14,8 м и величину перемещения: | Δ r → | = | S 1 − S 2 | = | 5,0 − 9,8 | = 4,8 м. Найдем искомое отношение пройденного пути и модуля перемещения: S | Δ r → | = 14,8 4,8 ≈ 3,1 . Пройденный путь приблизительно в 3,1 раза превышает величину перемещения.   Позвольте представиться. Меня зовут Татьяна. Я уже более 8 лет занимаюсь психологией. Считая себя профессионалом, хочу научить всех посетителей сайта решать разнообразные задачи. Все данные для сайта собраны и тщательно переработаны для того чтобы донести как можно доступнее всю необходимую информацию. Перед применением описанного на сайте всегда необходима ОБЯЗАТЕЛЬНАЯ консультация с профессионалами. |












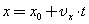
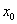
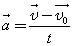
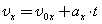
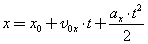
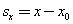
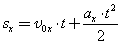
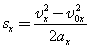
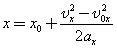
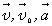
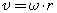
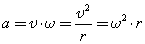
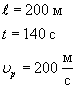

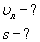
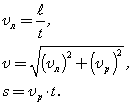
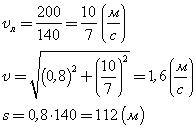

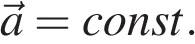
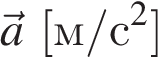 ) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.
) — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.