Уравнение парной линейной регрессии

Уравнение парной линейной регрессии

Пусть функционирование экономического объекта описывается двумя числовыми переменными: входной переменной X и выходной переменной Y. Возможно, что X может изменяться (регулироваться) исследователем, а значе­ние Y получается как результат функционирования объекта.

Предполагается, что Y зависит от X практически линейно:

где m и b – детерминированные величины, e – случайная величина.

Выходная переменная Y называется зависимой переменной (или объяс­няемой переменной, или откликом). Входная переменная X называется незави­симой переменной (или объясняющей пере­менной, или фактором, или регрес­сором). Случайную величину e в экономет­рике называют возмущением.

Если математическое ожидание возмущения равно нулю, то функция

является условным математическим ожиданием Y при заданном значении X=x: f(x)≡M_xY. В этом случае соотношение (1) называется регрессионным уравне­нием. Чтобы подчеркнуть, что переменных всего две, а связь между ними ли­нейная, говорят, что (1) – уравнение парной линейной регрессии. Функция f(x) называется регрессией (линейной) Y по X (или функцией регрессии), а величины m и b – параметрами линейной регрессии (m – коэффициентом, b – сдвигом).

Требуется по наблюдениям найти в некотором смысле наилучшие оцен­ки

и значений m и b. Если и получены, то оценку отклика по извест­ному значению фактора x можно определить по формуле:

. (2)

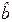
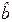
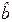
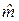
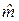
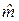
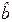
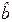
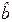
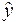
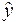
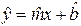
Формулу (2) можно использовать для прогноза значения отклика по инте­ресующему исследователя значению фактора.

Дата добавления: 2014-11-10 ; просмотров: 382 . Нарушение авторских прав

Решения задач: линейная регрессия и коэффициент корреляции

Парная линейная регрессия – это зависимость между одной переменной и средним значением другой переменной. Чаще всего модель записывается как $y=ax+b+e$, где $x$ – факторная переменная, $y$ – результативная (зависимая), $e$ – случайная компонента (остаток, отклонение).

В учебных задачах по математической статистике обычно используется следующий алгоритм для нахождения уравнения регрессии.

1. Выбор модели (уравнения). Часто модель задана заранее (найти линейную регрессию) или для подбора используют графический метод: строят диаграмму рассеяния и анализируют ее форму.
2. Вычисление коэффициентов (параметров) уравнения регрессии. Часто для этого используют метод наименьших квадратов.
3. Проверка значимости коэффициента корреляции и параметров модели (также для них можно построить доверительные интервалы), оценка качества модели по критерию Фишера.
4. Анализ остатков, вычисление стандартной ошибки регрессии, прогноз по модели (опционально).

Ниже вы найдете решения для парной регрессии (по рядам данных или корреляционной таблице, с разными дополнительными заданиями) и пару задач на определение и исследование коэффициента корреляции.

Примеры решений онлайн: линейная регрессия

Простая выборка

Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.

Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.

Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.

Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью.
Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.

Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

Корреляционная таблица

Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице

Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.

Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.

Коэффициент корреляции

Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?

Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $overline=82$ у.е., $S_x=31$ у.е., $overline=39$ у.е., $S_y=29$ у.е., $overline =3709$ (у.е.)2. При $alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.

Парная регрессия

Построение модели парной регрессия (или однофакторная модель) заключается в нахождении уравнения связи двух показателей у и х, т.е. определяется как повлияет изменение одного показателя на другой.

В задачах по эконометрике основным этапом является нахождение параметров модели и оценке их качества. Уравнение модели парной регрессии можно записать в общем виде:

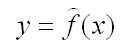
где у — зависимый показатель (результативный признак);

х — независимый, объясняющий фактор.

Линейные и нелинейные модели регрессии

Уравнение линейной регрессии: у = а + bx

Уравнения нелинейной регрессии

полиномиальная функция

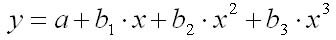
гиперболическая функция

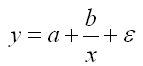
степенная модель

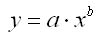
показательная модель

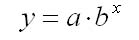
экспоненциальная модель

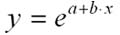
Пример на парную регрессию

Видео лекции по моделям парной регрессии

Для более подробного изучения моделей парной регрессии советуем посмотреть это видео

Определение параметров в моделях парной регрессии

Нахождение модели парной регрессии в эконометрике сводится к оценке уравнения в целом и по параметрам (a, b). Для оценки параметров однофакторной линейной модели используют метод наименьших квадратов (МНК). В МНК получается, что сумма квадратов отклонений фактических значений показателя у от теоретических ух минимальна

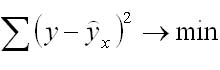
Сущность нелинейных уравнений, которые находятся в том случае, если нет линейных моделей, заключается в приведении их к линейному виду и как при линейных уравнениях решается система относительно коэффициентов a и b.

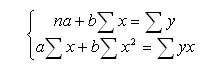
Для нахождения коэффициентов a и b в уравнении модели парной регрессии можно использовать формулы.

Уравнение парной линейной регрессии

Пусть функционирование экономического объекта описывается двумя числовыми переменными: входной переменной X и выходной переменной Y. Возможно, что X может изменяться (регулироваться) исследователем, а значе­ние Y получается как результат функционирования объекта.

Предполагается, что Y зависит от X практически линейно:

где m и b – детерминированные величины, e – случайная величина.

Выходная переменная Y называется зависимой переменной (или объяс­няемой переменной, или откликом). Входная переменная X называется незави­симой переменной (или объясняющей пере­менной, или фактором, или регрес­сором). Случайную величину e в экономет­рике называют возмущением.

Если математическое ожидание возмущения равно нулю, то функция

является условным математическим ожиданием Y при заданном значении X=x: f(x)≡M_xY. В этом случае соотношение (1) называется регрессионным уравне­нием. Чтобы подчеркнуть, что переменных всего две, а связь между ними ли­нейная, говорят, что (1) – уравнение парной линейной регрессии. Функция f(x) называется регрессией (линейной) Y по X (или функцией регрессии), а величины m и b – параметрами линейной регрессии (m – коэффициентом, b – сдвигом).

Требуется по наблюдениям найти в некотором смысле наилучшие оцен­ки

и значений m и b. Если и получены, то оценку отклика по извест­ному значению фактора x можно определить по формуле:

. (2)

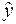
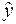
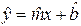
Формулу (2) можно использовать для прогноза значения отклика по инте­ресующему исследователя значению фактора.

Оценивание параметров уравнения линейной регрессии

Для получения оценок

и традиционно используется метод наимень­ших квадратов (МНК). В соответствии с МНК значения и определяются из условия минимума остаточной суммы, которая равна сумме квадратов от­клонений наблюдений отклика y_i от оценок, полученных с помощью соотношения (2).

Обозначим:

– оценка отклика для i-го наблюдения, i=1, …, n; – отклонение наблюдения отклика от оценки; величины e_i называются остатками; Q_e – остаточная сумма.

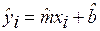
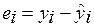
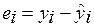
Графически определение остатков поясняется на рис. 1. Координатная плоскость, на которой нанесены точки наблюдений, назы­вается полем корреляции.

С учетом принятых обозначений остаточная сумма является суммой квадратов остатков и задается формулой:

(3)

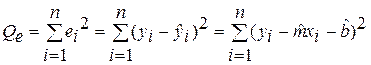
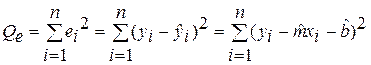
Ясно, что чем меньше Q_e, тем лучше оценки соответствуют наблюдениям. Из необ­ходимого условия экстремума Q_e (равенства ча­стных производных по

и нулю) можно получить формулы для оценок параметров уравнения линейной регрессии:

, (4)

. (5)

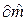
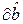
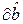
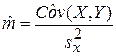
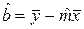
В формулах (4) и (5) использованы обозначения:

– выборочная ковариация переменных X и Y, – выборочная дисперсия переменной X, и – выборочные средние значения X и Y, соответственно.

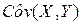
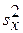
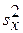
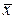
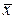
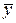
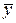
Определения перечисленных выше выборочных характеристик приводятся в Приложении. Вывод формул (4) и (5) дается, например, в [5].

Понятие тесноты связи

Заметим, что сдвиг b нельзя считать объективной характеристикой зависимости Y от X, потому что его величина определяется выбором начала координат. Из соотношения (5), в частности, следует, что для МНК-оценок

прямая, задаваемая уравнением (2), всегда проходит через точку ( ). Подставив (5) в (2), после несложных преобразований получим:

. (6)

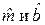
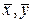
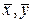
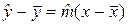
Это соотношение связывает отклонения оценки отклика и фактора от их выборочных средних значений. Переход от величин к их отклонениям от сред­него называется центрированием этих величин. Заметим, что значение

в соот­ношении (6) не присутствует.

На первый взгляд кажется, что по величине коэффициента

можно су­дить о степени зависимости Y от X: чем больше , тем сильнее зависимость. Это не совсем так, потому что на величину влияет выбор единиц измерения X и Y. Для получения более объективной, чем , характеристики зависимости X и Y,следует найти связь между их нормированными значениями. Нормировку обычно проводят делением величины X (и, соответственно, Y) на ее выбороч­ное среднее квадратичное отклонение s_x (s_y). Разделим обе части соотноше­ния (6) на s_y, а затем правую часть умножим и разделим на s_x. Тогда получим:

(7)

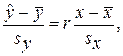
где введено обозначение:

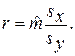
Величина r называется выборочным коэффициентом корреляции (см. Приложение). Коэффициент r показывает, на сколько значений s_y в среднем увеличится отклик, если фактор увеличится на s_x. Говорят, что выборочный коэффициент корреляции характеризует тесноту связи между X и Y.

Известно, что |r| ≤1. Чем ближе |r| к 1, тем теснее связь между X и Y; чем ближе |r| к 0, тем слабее связь. При r=±1 точки наблюдений лежат на прямой, задаваемой соотношением (2). При r=0 прямая (2) параллельна оси абсцисс, и связь между X и Y отсутствует. Примеры тесной и слабой связи даны на рис.2.

Линейная парная регрессия (стр. 1 из 4)

1. Линейная парная регрессия

Корреляционная зависимость может быть представлена в виде

В регрессионном анализе рассматривается односторонняя зависимость случайной переменной Y от одной (или нескольких) неслучайной независимой переменной Х . Такая зависимость Y от X (иногда ее называют регрессионной ) может быть также представлена в виде модельного уравнения регрессии Y от X (1). При этом зависимую переменную Y называют также функцией отклика (объясняемой, выходной, результирующей, эндогенной переменной, результативным признаком), а независимую переменную Х – объясняющей (входной, предсказывающей, предикторной, экзогенной переменной, фактором, регрессором, факторным признаком).

Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная Х примет значение х , т.е. Х = х . В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (x_i , y_i ) ограниченного объема n . В этом случае речь может идти об оценке (приближенном выражении, аппроксимации) по выборке функции регрессии. Такой оценкой является выборочная линия (кривая) регрессии :

Уравнение (2) называется выборочным уравнением регрессии .

В дальнейшем рассмотрим линейную модель и представим ее в виде

Для решения поставленной задачи определим формулы расчета неизвестных параметров уравнения линейной регрессии (b , b ₁ ).

Согласно методу наименьших квадратов (МНК) неизвестные параметры b и b ₁ выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значенийy_i от значений

На основании необходимого условия экстремума функции двух переменных S = S (b , b ₁ ) (4) приравняем к нулю ее частные производные, т.е.

откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:

Теперь, разделив обе части уравнений (5) на n , получим систему нормальных уравнений в следующем виде:

где соответствующие средние определяются по формулам:

Решая систему (6), найдем

Коэффициент b ₁ называется выборочным коэффициентом регрессии Y по X .

Коэффициент регрессии Y по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.

Отметим, что из уравнения регрессии

На первый взгляд, подходящим измерителем тесноты связи Y от Х является коэффициент регрессии b ₁ . Однако b ₁ зависит от единиц измерения переменных. Очевидно, что для “исправления” b ₁ как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Если представить уравнение

В этой системе величина

Если r > 0 (b ₁ > 0), то корреляционная связь между переменными называется прямой, если r 2 . (20)

4. Возмущения e_i и e_j не коррелированны:

5. Возмущения e_i есть нормально распределенная случайная величина.

Оценкой модели (18) по выборке является уравнение регрессии

Теорема Гаусса – Маркова . Если регрессионная модель
y_i = b + b₁x_i + e_i удовлетворяет предпосылкам 1-5, то оценкиb , b ₁ имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Таким образом, оценки b и b ₁ в определенном смысле являются наиболее эффективными линейными оценками параметров b и b₁ .

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Для проверки значимости выдвигают нулевую гипотезу о надежности параметров. Вспомним основные понятия и определения необходимые для анализа значимости параметров регрессии.

Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным.

Уравнение парной линейной регрессии

Параметры уравнения y = a*x + b

а) с помощью статистической функции ЛИНЕЙН (Excel). Получаем следующую статистику:

a	0,15	197,80	b
ma	0,07	13,77	mb
R 2	0,32	8,36	Sост
Fф	5,07	11	Ч.С.С
354,56	768,52	(y-y x ) 2

Записываем уравнение парной линейной регрессии:

Экономический смысл уравнения: с увеличением х на 1 ед., y возрастает в среднем на а ед.

Если требуется рассчитывать без применения Excel, то строим таблицу.

N	x	y	x 2	x*y	(y-y x ) 2	(y-y ср ) 2
1
2
3
N
Итого
Среднее

б) для парной линейной регрессии:

в) или решая систему уравнений

Для автоматического расчета можно воспользоваться сервисом Уравнение регрессии

б) с помощью статистической функции КОРРЕЛ (Excel)

в) по формуле:
или

К xy – корреляционный момент (коэффициент ковариации)

Средняя ошибка аппроксимации (рассчитываем столбцы y x , y i -y x , A i )

Это означает, что в среднем, расчетные значения зависимого признака отклоняются от фактического значения на А%.

а) с помощью функции ЛИНЕЙН (Excel)

б) R 2 = r 2 xy ; R 2 = 0,32, т.е. в 31,57% случаев изменения х приводят к изменению y . Другими словами – точность подбора уравнения регрессии 31,57% – низкая.

Оценка статистической значимости
а) по критерию Фишера :

1. Выдвигаем нулевую гипотезу о статистической незначимости параметров регрессии и показателя корреляции а = b = r xy

2. Фактическое значение критерия получено из функции ЛИНЕЙН (Excel)

3.Для определения табличного значения критерия рассчитываем коэффициенты k₁ = m = 1 и k₂= n – m – 1

4. Сравниваем фактическое и табличное, значения критерия F факт > F табл
нулевую гипотезу отклоняем и делаем вывод о статистической значимости и надежности полученной модели.

б) по критерию Стъюдента

1. Выдвигаем нулевую гипотезу о статистически незначимом отличии показателей от нуля; а = b = r xy =0;

2. Табличное значение t-критерия зависит от числа степеней свободы и заданного уровня значимости а.

Уровень значимости – это вероятность отвергнуть правильную гипотезу при условии, что она верна.

3. Фактические значения t-критерия рассчитываются отдельно для каждого параметра модели. С этой целью, сначала определяются случайные ошибки параметров m_a, m_b, mr

S 2 – необъясненная дисперсия является несмещенной оценкой дисперсии случайных отклонений

n – число наблюдений, m – число независимых переменных.

Рассчитаем фактические значения t-критерия.

4. Сравниваем фактические значения t-критерия с табличными значением:

нулевую гипотезу отклоняем, параметры a = b = r xy – не случайно отличаются от нуля и являются статистически значимыми и надежными.

в) чтобы рассчитать доверительный интервал для параметров регрессии a,b необходимо определить предельную ошибку параметров:

а ± ∆a; a – ∆a ≤ a ≤ a + ∆a

b ± ∆b; b – ∆b ≤ b ≤ b + ∆b

Анализ верхней и нижней границ доверительного интервалов показывает, что с вероятностью р = 1- α = 0,95 параметры а и b не принимают нулевые значения, т.е. являются статистически значимыми и надежными. Если одна из границ доверительного интервала – меньше нуля или равна нулю – делается вывод о статистической незначимости соответствующего параметра.

4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Прогнозное значение y_p определятся путем подстановки в уравнение регрессии соответствующего прогнозного значения х_р. Если прогнозное значение составит х_р = ∙1,1, то прогнозное значение y

5. Рассчитаем случайную ошибку прогноза:

Предельная ошибка прогноза: ∆y = t_табл*m_yp

Доверительный интервал прогноза:

С надежностью 0,95 прогнозное значение y заключено в данном доверительном интервале. Поскольку границы не принимают нулевых значений можно сделать вывод о статистической надежности прогноза.

Автоматический расчет

Для автоматического расчета можно воспользоваться сервисом Уравнение регрессии. Необходимо будет ввести значения x,y (можно вставить из MS Excel). Решение оформляется в файле MS Word с пояснением нахождения каждого параметра.

Уравнение парной регрессии. Руководство к решению задач

Наблюдение	Объем товарооборота, млн. руб.	Число работников
1	0,5	73
2	0,7	85
3	0,9	102
4	1,1	115
5	1,4	122
6	1,4	126
7	1,7	134
8	1,9	147

Построить регрессионную модель зависимости объема товарооборота от числа работников. Проверить значимость модели и коэффициентов модели. Рассчитать коэффициент эластичности и дать ему экономическую интерпретацию. Построить 95% доверительный интервал для оценки объема товарооборота отдельного магазина со 100 работниками.

Решение:
Для решения используем сервис «Уравнение парной регрессии». Исходные данные можно ввести вручную (при этом необходимо указать параметр Количество строк: 8) или вставить данные из Excel. Уровень значимости устанавливаем как 0.05 .
Поскольку необходимо найти зависимость объема товарооборота от числа работников, то в качестве Y – принимаем Объем товарооборота, X – Число работников.

На следующем шаге определяем параметры отчета: t-статистика. Критерий Стьюдента, F-статистика. Критерий Фишера.
Получаем таблицу вида:

x	y	x 2	y 2	x•y	y(x)	(yi-ycp) 2	(y-y(x)) 2	(xi-xcp) 2	|y – yx|:y
73	0.5	5329	0.25	36.5	0.43	0.49	0.004832	1600	0.14
85	0.7	7225	0.49	59.5	0.66	0.25	0.001495	784	0.0552
102	0.9	10404	0.81	91.8	0.99	0.09	0.007812	121	0.0982
115	1.1	13225	1.21	126.5	1.24	0.01	0.0192	4	0.13
122	1.4	14884	1.96	170.8	1.37	0.04	0.000721	81	0.0192
126	1.4	15876	1.96	176.4	1.45	0.04	0.002509	169	0.0358
134	1.7	17956	2.89	227.8	1.6	0.25	0.009217	441	0.0565
147	1.9	21609	3.61	279.3	1.85	0.49	0.002108	1156	0.0242
904	9.6	106508	13.18	1168.6	9.6	1.66	0.0479	4356	0.55

здесь столбцы 1-5 используются для вычисления остальных столбцов таблицы.
y(x) – определяется по найденным коэффициентам регрессии как y(x) = bx + a и используется для вычисления столбцов 8 и 10.
(y_i-y_cp) 2 , (y-y(x)) 2 – значения столбцов используются для вычисления коэффициента детерминации R 2 (п. 1.5. и 2.5.2 отчета).
(x_i-x_cp) 2 – используется для построения доверительного интервала зависимой переменой (п.2.4. отчета)
|y – y_x|:y – используется при вычислении ошибки аппроксимации.

Если вычисление каких-либо коэффициентов не запланировано заданием, соответствующие столбцы можно удалить (обычно это столбцы 9 и 10).

Регрессионная модель имеет вид: y = 0.0192x – 0.97

Автоматически строится поле корреляции.

Задание 2. Имеются следующие данные о связи между произведенной продукцией (в отпускных ценах) и переработкой сырья по 12 предприятиям:

Номер предприятия	1	2	3	4	5	6	7	8	9	10	11	12
Валовая продукция, млрд р.	2,4	2,8	3,4	3,6	4,0	4,4	4,8	5,3	5,5	6,0	6,2	6,5
Переработано сырья, тыс. ц	0,6	0,9	1,2	0,8	1,4	1,8	1,6	2,0	2,4	2,7	2,9	3,2

Составьте линейное уравнение регрессии, вычислите параметры и оцените тесноту корреляционной связи.

Решение:
В качестве факторной переменной X принимаем параметр Переработано сырья (тыс. ц), в качестве зависимой переменной Y – Валовая продукция ( млрд р.). Подготовим данные для вставки из Excel. Для этого скопируем таблицу в Excel и транспонируем с помощью функции ТРАНСП .

В ячейку А5 записываем формулу
=ТРАНСП(A1:M3)
Выделяем диапазон А5:С17 и нажимаем F2 , а затем сочетание клавиш Enter+Shift+Ctrl .

Задание 3. По данным задачи 6 для изучения тесноты связи между средними товарными запасами (результативный признак Y) и оборотом розничной торговли (факторный признак) вычислите эмпирическое корреляционное отношение. Сделайте выводы.
Решение:
Эмпирическое корреляционное отношение рассчитывается в п.1.5.

Задание 4. Имеются выборочные данные по однородным предприятиям: энерговооруженность труда одного рабочего (кВт/час) и выпуск готовой продукции (шт). Определить:

1. Факторные и результативные признаки.
2. Провести исследование взаимосвязи энерговооруженности и выпуска готовой продукции.
3. Найти коэффициент регрессии и построить уравнение регрессии.
4. Построить графики практической и теоретической линии регрессии.
5. Определить форму связи и измерить тесноту связи.
6. Провести оценку адекватности регрессионной модели с помощью критерия Фишера.

Решение:
В данном случае в качестве факторного признака выступает энерговооруженность труда одного рабочего (X), а результативный признак – выпуск готовой продукции (Y).
Коэффициент регрессии для уравнения y = bx + a определяется значением b (см. п. 1.2 отчета или расчеты на основе МНК). Графики практической и теоретической линии регрессии удобней строить средствами Excel. Форму связи можно определить исходя из графика. Измерение тесноты связи и ее анализ см. в п.1.2 отчета.
Оценка адекватности регрессионной модели проводится в п.2.5 (раздел №2: F-статистика. Критерий Фишера).

Задание 4. Экономист, изучая зависимость уровня Y (тыс. руб.) издержек обращения от объема X (тыс. руб.) товарооборота, обследовал по 10 магазинов, торгующих одинаковым ассортиментом товаров в 5 районах. Полученные данные отражены в таблице 1. Задание. Для каждого из районов (в каждой задаче) требуется:

• найти коэффициенты корреляции между X и Y ;
• построить регрессионные функции линейной зависимости Y = a + b*X фактора Y от фактора X и исследовать их на надежность по критерию Фишера при уровне значимости 0.05 ;
• найти коэффициент эластичности Y по X при среднем значении X ;
• определить надежность коэффициентов регрессии по критерию Стьюдента:
• найти доверительные интервалы для коэффициентов регрессии;
• построить график регрессионной функции и диаграмму рассеяния;
• используя полученное уравнение линейной регрессии, оценить ожидаемое среднее значение признака Y при X = 130 тыс. руб.

Решение: Уровень значимости оставляем по умолчанию ( 0.05 ), значение зависимой переменной устанавливаем как 130 . Вставляем данные через кнопку Вставить из Excel .
Включать в отчет: t-статистика. Критерий Стьюдента, F-статистика. Критерий Фишера.

Парная регрессия (стр. 1 из 5)

Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х₁ , Х₂ , … Х_р и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.

Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.

Парная регрессия – уравнение связи двух переменных у иx :

где у – зависимая переменная (результативный признак);

х – независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

• полиномы разных степеней

Регрессии, нелинейные по оцениваемым параметрам:

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b :

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции

и индекс корреляции

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

Допустимый предел значений

Средний коэффициент эластичности

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :

Коэффициент детерминации – квадрат коэффициента или индекса корреляции.

F -тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Н_о о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F -критерия Фишера. F _факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

п – число единиц совокупности;

т – число параметров при переменных х.

F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.

Если F_табл F_факт , то гипотеза Н не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и критическое (табличное) значения t-статистики – t_табл и t_факт – принимаем или отвергаем гипотезу H_о .

Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством

Если t_табл t_факт , то гипотеза Н_о не отклоняется и признается случайная природа формирования a , b или

Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:

Формулы для расчета доверительных интервалов имеют следующий вид:

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

и строится доверительный интервал прогноза:

По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):