Чертеж из 3 проекций

Способы построения видов на чертеже

Построение видов начинается с мысленного выбора положе­ния детали перед плоскостями проекций. Затем выбирают коли­чество видов, необходимых и достаточных для выявления формы детали, а также способ их построения.

Выбор положения детали в системе плоскостей проекций за­висит от ее рабочего положения, способа изготовления на произ­водстве, формы. Например, если деталь изготавливается на то­карном станке, то на чертеже ее ось вращения должна распола­гаться горизонтально.

Виды чертежа могут быть выполнены различными способами. Рассмотрим некоторые из них.

Построение видов на основе последовательного вычерчива­ния геометрических тел, составляющих форму предмета. Для того чтобы выполнить чертеж этим способом, необходимо мысленно разделить деталь на составляющие ее простые геометри­ческие тела, выяснив, как они расположены относительно друг друга. Затем нужно выбрать главный вид детали и число изо­бражений, позволяющие понять ее форму и последовательно изобразить одно геометрическое тело за другим до полного ото­бражения формы объекта. Необходимо соблюдать размеры фор­мы и правильно ориентировать ее элементы относительно друг друга (табл. 8).

Построение видов на основе поэлементного вычерчивания геометрических тел, составляющих форму предмета, осуществля­ется с помощью приемов удаления и приращения.

При вычерчивании геометрического тела с использованием приема удаления на чертеже последовательно изменяется форма заготовки с помощью удаления объемов схожих с приемами ее обработки точением, сверлением, фрезерованием и т. п.

При вычерчивании геометрического тела с использованием приема приращения объемы элементов изделия как бы допол­няют друг друга, приращиваются.

8. Поэлементное вычерчивание геометрических тел, составляющих форму предмета

Построение видов с помощью постоянной прямой чертежа (способ внешнего координирования). Постоянной прямой чер­тежа называют линию, которую проводят из центра координат (точки О) вниз направо под углом 45° (рис. 86).

Предмет мысленно размещают в системе плоскостей проек­ций. Оси плоскостей проекций принимают за координатные оси. Проекционную связь между видом сверху и видом слева осуще­ствляют с помощью линий проекционной связи, которые прово­дят до пересечения с постоянной прямой чертежа и строят под углом 90° друг к другу.

Постоянную прямую чертежа, как правило, используют в тех случаях, когда по двум заданным видам необходимо построить третий вид детали (см. рис. 86). Перечертив два вида детали, строят постоянную прямую чертежа и проводят линии проекци­онной связи параллельно оси ОХ до пересечения с постоянной прямой чертежа, а затем — параллельно оси OZ.

Рассмотренный способ построения называют способом внеш­него координирования, поскольку предмет фиксируется в про­странстве относительно осей плоскостей проекций, которые рас­полагаются вне изображаемого объекта.

(Если на чертеже не показаны оси проекций и необходи­мо выполнить третий вид детали, то можно построить постоян­ную прямую чертежа в любом месте с правой стороны от вида сверху.)

Построение видов с помощью внутреннего координирования объекта. Внутреннее координирование заключается в мысленном введении дополнительных осей координат, привязанных к проецируемому предмету.

Рис. 86. Построение третьей проекции по двум заданным с помощью постоянной прямой чертежа

Рис. 87. Построение видов способом внутреннего координирования объекта

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

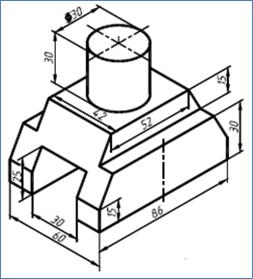
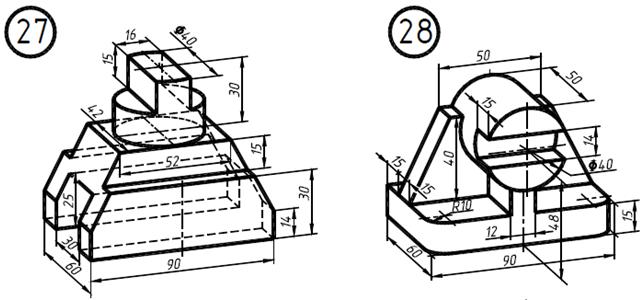
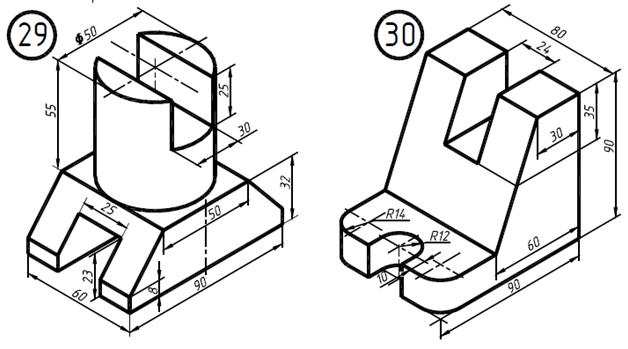
Выполнение чертежа трех видов по данному наглядному изображению детали.

1. Внимательно ознакомиться с конструкцией детали по ее наглядному изображению и определить основные геометрические тела, из которых она состоит.

2. Выбрать главное изображение. Согласно ГОСТ 2.305-2008, изображение на фронтальнойплоскости проекций принимают на чертеже в качестве главного. Деталь располагают относительно фронтальной плоскости проекций так, чтобы изображение на ней давало наиболее полное представление о форме и размерах предмета. При этом максимальное количество геометрических фигур, образующих деталь, имеет оси вращения, параллельные фронтальной плоскости,а плоскость основания детали располагается параллельно горизонтальной плоскости проекций.

В зависимости от содержания главное изображение может быть видом, разрезом, или соединением половины вида спереди с половиной фронтального разреза. В работе изображение – вид спереди.

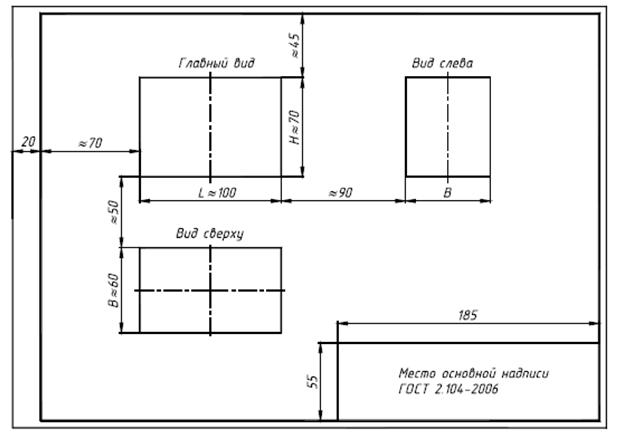
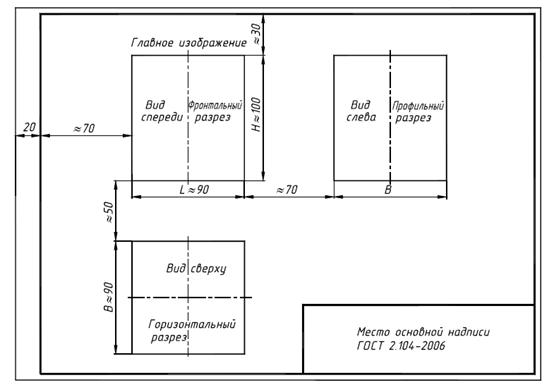
3. Выделить на листе ватмана соответствующую площадь для каждого из трех видов (видаспереди – главное изображение, вида сверху и вида слева). При этом обратить внимание на то,что изображения детали (виды) должны располагаться на листе равномерно, а не концентрироваться в одном углу. Расстояния между отдельными изображениями и самих изображений отлиний рамки должны выбираться такими, чтобы обеспечить условия для нанесения размеров,условных обозначений и надписей. Провести штрихпунктирные линии: оси поверхностей вращения, оси симметрии изображений. Осевые линии должны выходить за контур изображения не далее пяти мм.

4. Построить три вида детали в тонких линиях, соблюдая проекционную связь. Штриховыми линиями показать внутренний контур детали.

5. Нанести выносные и размерные линии, стрелки, проставить размерные числа, знакидиаметров, радиусов, уклонов и конусности (ГОСТ 2.307-2011).

При выполнении задания № 2 используется упрощенный геометрический принцип задания размеров на чертеже.

Расстояния между крайними точками детали по длине, высоте и ширине называют габаритными размерами. Габаритные размеры должны проставляться на каждом чертеже.

Проверить правильность выполненных изображений.

6. Обвести чертеж линиями требуемой толщины (ГОСТ 2.303-68). Линии видимого контурадолжны быть толщиной не менее 0,5 мм. Линии невидимого контура и осевые должны быть в 2…3раза тоньше.

7. Заполнить основную надпись чертежа в соответствии с ГОСТ 2.104-2006.

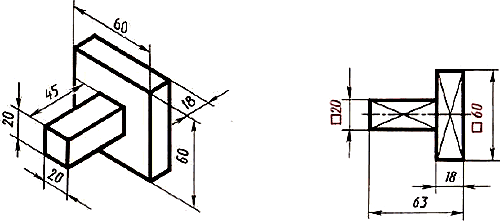
Рис. 22. Наглядное изображение одной из возможных деталей

Рис. 23. Пример выполнения чертежа «Виды»

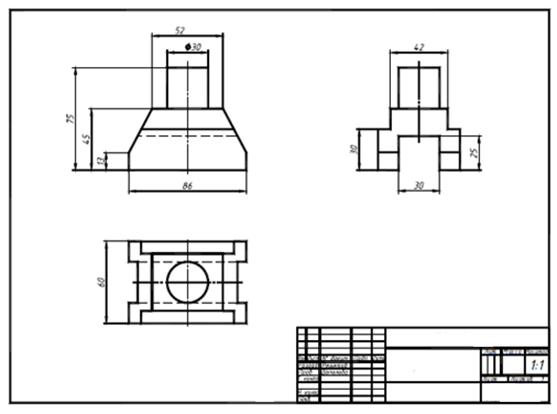
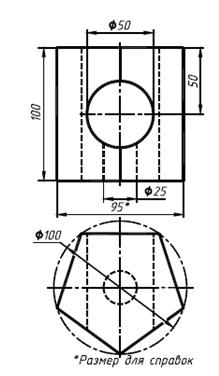
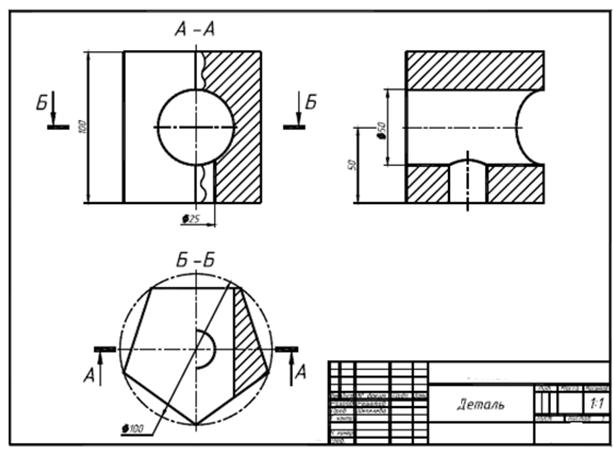
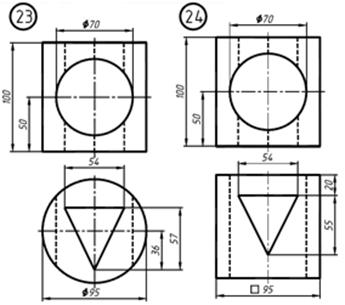
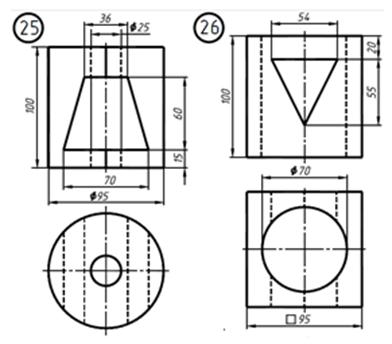
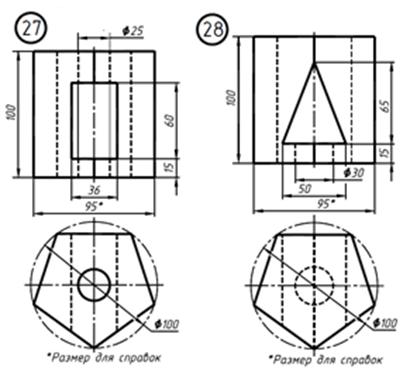
По двум заданным проекциям детали построить три её изображения. Применить вертикальные и горизонтальные разрезы. Нанести размеры.

Порядок выполнения

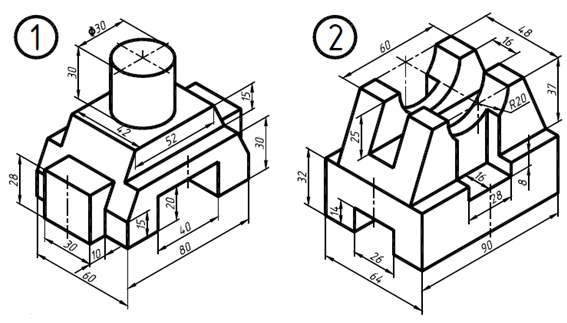
1. Внимательно ознакомиться с конструкцией детали по двум заданным проекциям детали и определить основные геометрические тела, из которых она состоит.

2. Выделить на листе ватмана соответствующую площадь для каждого из трех изображений (см. рис. ниже). Главное изображение – соединение половины вида спереди с половиной фронтального разреза. На месте вида сверху – соединение половины вида с половиной горизонтального разреза. На месте вида слева выполнить соединение половины вида с половиной профильного разреза. При этом обратить внимание на то, что изображения детали должны располагаться на листе равномерно, а не концентрироваться в одном углу. Расстояния между отдельными изображениями и самих изображений от линий рамки должны выбираться такими, чтобы обеспечить условия для нанесения размеров, условных обозначений и надписей. Провести штрихпунктирные линии: оси поверхностей вращения, оси симметрии изображений.

3. Построить три изображения детали в тонких линиях, соблюдая проекционную связь. При соединении половины вида с половиной разреза не показывают штриховыми линиями внутренний контур детали.

4. Нанести выносные и размерные линии, стрелки, проставить размерные числа, знакидиаметров, радиусов, уклонов и конусности (ГОСТ 2.307-2011.

5. Проверить правильность выполненных изображений.

6. Обвести чертеж линиями требуемой толщины(ГОСТ 2.303-68).

7. Заполнить основную надпись чертежа в соответствии сГОСТ 2.104-2006.

На рис. 25 представлены две проекции одной из возможныхвариантов деталей, а на рис. 26 дан пример выполнения ее чертежа. На главном изображении вид отделен от фронтального разрезаволнистой линией, проведенной правее оси симметрии, так как награницу попало ребро призмы.

На месте вида слева выполнен полный профильный разрез, таккак относительно П3 деталь не является симметричной фигурой.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ – конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

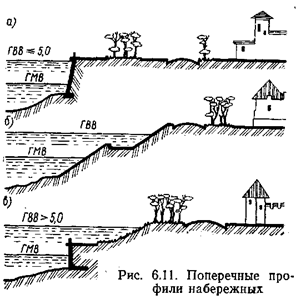
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

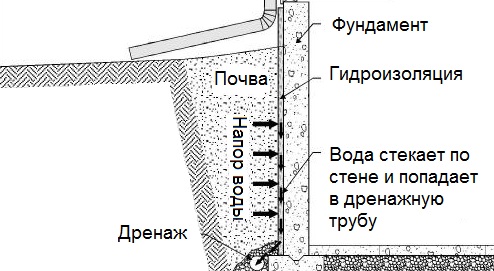
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Чертеж из 3 проекций

Эпюр – Чертеж из трех проекций

Разбор по буквам:

• Эпюр – Слово на Э
• 1 – я буква Э
• 2 – я буква П
• 3 – я буква Ю
• 4 – я буква Р

Варианты вопросов:

translateSpanWord

Кроссворды, сканворды – доступный и действенный способ тренировки интеллекта, увеличения багажа знаний. Разгадывать слова, складывать пазлы – развивать логическое и образное мышление, стимулировать нейронную деятельность мозга и, наконец, с удовольствием коротать свободное время.

§ 11. Чертежи и аксонометрические проекции геометрических тел

Итак, вы уже знаете, что форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела.

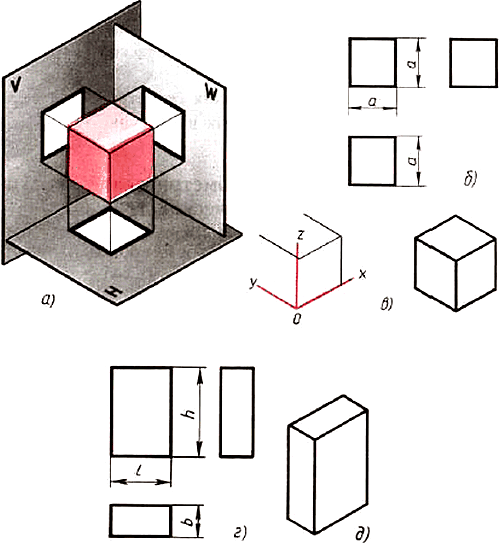
11.1. Проецирование куба и прямоугольного параллелепипеда. Куб располагают так, чтобы его грани были параллельны плоскостям проекций. Тогда они изобразятся на параллельных им плоскостях проекций в натуральную величину — квадратами, а на перпендикулярных плоскостях отрезками прямых (рис. 76).

Рис. 76. Куб и параллелепипед: а — проецирование: б, г — чертежи в системе прямоугольных проекций: в, д — изометрические проекции

Проекциями куба являются три равных квадрата.

На чертеже куба и параллелепипеда указывают три размера: длину, высоту и ширину.

На рисунке 77 деталь образована двумя прямоугольными параллелепипедами, имеющими по две квадратные грани. Обратите внимание, как нанесены на чертеже размеры. Плоские поверхности отмечены тонкими пересекающимися линиями.

Рис. 77. Изображение детали в одном виде

Благодаря условному знаку форма детали ясна и по одному виду.

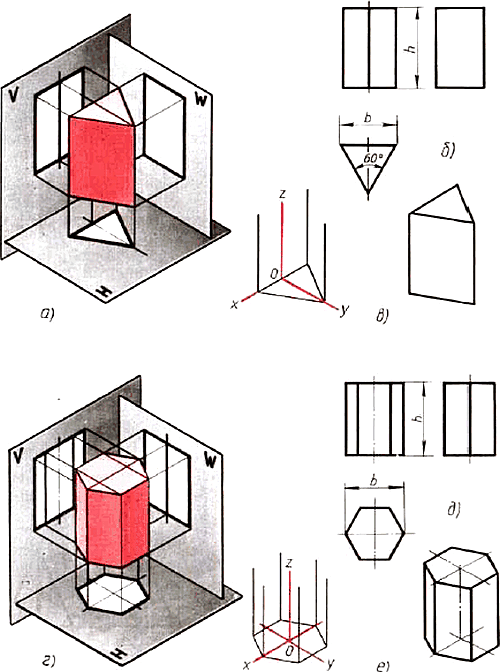
11.2. Проецирование правильных треугольной и шестиугольной призм. Основания призм, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых на тех, которым они перпендикулярны (рис. 78). Грани. наклоненные к плоскостям проекций, изображаются на них искаженными.

Рис 78. Призмы: а. г — проецирование; б, д — чертежи в системе прямоугольных проекции: в, с – изометрические проекции

Размеры призм определяются их высотой и размерами фигуры основания. Штрихпунктирнымн линиями на чертеже проведены оси симметрии.

Строить изометрические проекции призмы начинают с основания. Затем из каждой вершины основания проводят перпендикуляры, на которых откладывают отрезки, равные высоте, и через полученные точки проводят прямые, параллельные ребрам основания.

Чертеж в системе прямоугольных проекций также начинают выполнять с горизонтальной проекции.

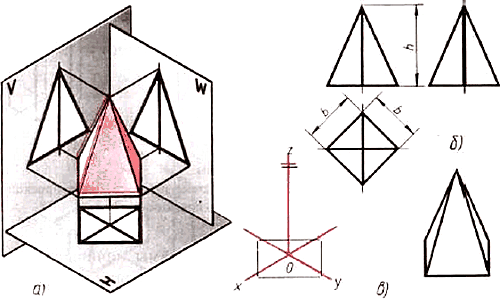
11.3. Проецирование правильной четырехугольной пирамиды. Квадратное основание пирамиды проецируется на горизонтальную плоскость Н в натуральную величину. На нем диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис. 79).

Рис. 79. Пирамида: проецирование: б чертеж в системе прямоугольных проекций; в изометрический проекции

Фронтальная и профильная проекции пирамиды — равнобедренные треугольники.

Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h.

Изометрическую проекцию пирамиды начинают строить с основания. Из центра полученной фигуры проводят перпендикуляр, откладывают на нем высоту пирамиды и соединяют полученную точку с вершинами основания.

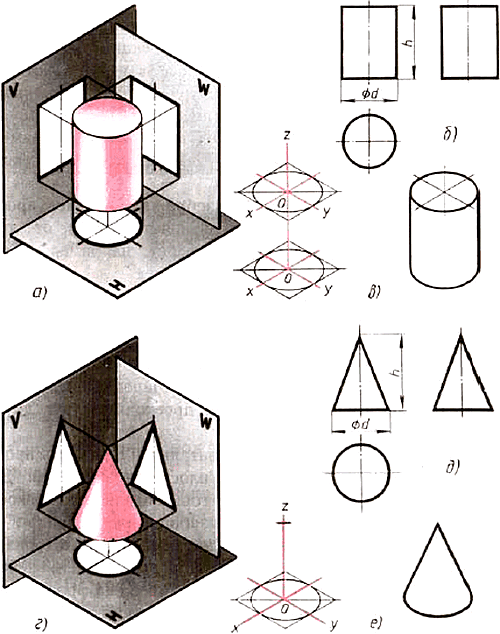
11.4. Проецирование цилиндра и конуса. Если круги, лежащие и основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости H, их проекции на эту плоскость будут также кругами (рис. 80, б и д).

Рис. 80. Цилиндр и конус: а, г — проецирование; б, д чертежи в системе прямоугольных проекций; в. е — изометрические проекции

Фронтальная и профильная проекции цилиндра в этом случае прямоугольники, а конуса — равнобедренные треугольники.

Заметьте, что на всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса.

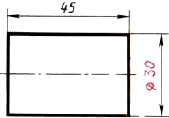
Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря значку “диаметр” можно представить форму цилиндра по одной проекции (рис. 81). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях.

Рис. 81. Изображение цилиндра в одном виде

Размеры цилиндра и конуса определяются их высотой h и диаметром основания d. Способы построения изометрической проекции цилиндра и конуса одинаковы. Для этого проводят оси х и у, на которых строят ромб. Стороны его равны диаметру основания цилиндра или конуса. В ромб вписывают овал (см. рис. 66).

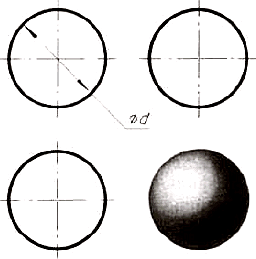
11.5. Проекции шара. Все проекции шара — круги, диаметр которых равен диаметру шара (рис. 82). На каждой проекции проводят центровые линии.

Рис. 82. Проекции шара

Благодаря знаку “диаметр” шар можно изображать в одной проекции. Но если по чертежу трудно отличить сферу от других поверхностей, добавляют слово «сфера», например: «Сфера диаметром 45».

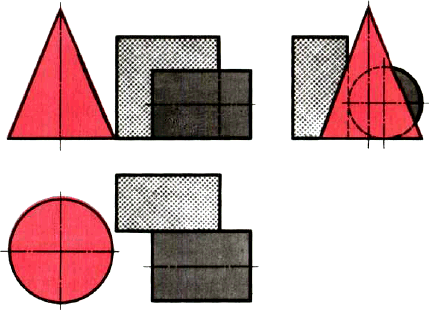
11.6. Проекции группы геометрических тел. На рисунке 83 даны проекции группы геометрических тел. Можете ли вы сказать, сколько геометрических тел входит в эту группу? Какие это тела?

Рис. 83. Чертеж группы геометрических тел

Рассмотрев изображения, можно установить, что на нем даны конус, цилиндр и прямоугольный параллелепипед. Они различно расположены относительно плоскостей проекций и друг друга. Как именно?

Ось конуса перпендикулярна горизонтальной плоскости проекций, а ось цилиндра — профильной плоскости проекций. Две грани параллелепипеда параллельны горизонтальной плоскости проекций. На профильной проекции изображение цилиндра находится справа от изображения параллелепипеда, а на горизонтальной — ниже. Это значит, что цилиндр расположен впереди параллелепипеда, поэтому часть параллелепипеда на фронтальной проекции показана штриховой линией. По горизонтальной и профильной проекциям можно установить, что цилиндр касается параллелепипеда.

Фронтальная проекция конуса касается проекции параллелепипеда. Однако, судя по горизонтальной проекции, параллелепипед не касается конуса. Конус расположен левее цилиндра и параллелепипеда. На профильной проекции он частично их закрывает. Поэтому невидимые участки цилиндра и параллелепипеда показаны штриховыми линиями.

Как изменится профильная проекция на рисунке 83, если из группы геометрических тел удалить конус?

Занимательные задачи

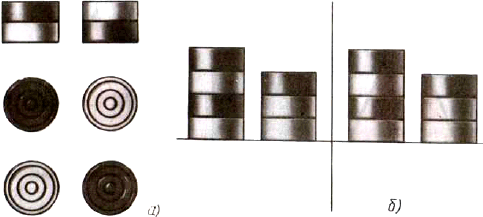
На столе лежат шашки, как показано на рисунке 84, а. Сосчитайте по чертежу, сколько шашек находится в первых ближних к вам столбиках. Сколько всего шашек лежит на столе? Если вы затрудняетесь сосчитать их по чертежу, попробуйте сначала сложить шашки в столбики, пользуясь чертежом. Теперь попробуйте правильно ответить на вопросы.

Рис. 84. Задания для упражнений

На столе в четыре столбика расположены шашки. На чертеже они показаны двумя проекциями (рис. 84, б). Сколько шашек на столе, если черных и белых поровну? Для решения этой задачи нужно не только знать правила проецирования, но и уметь логически рассуждать.

§ 8. Чертежи в системе прямоугольных проекций

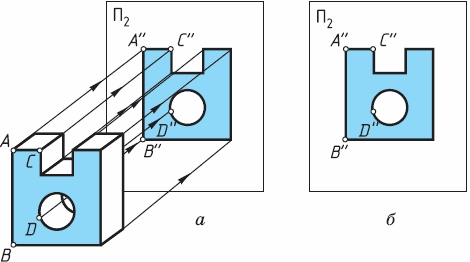
8.1. Прямоугольное проецирование на одну плоскость проекций. Пусть необходимо построить прямоугольную проекцию заданного предмета (рис. 31, а). Выберем для этой цели некоторую вертикальную плоскость проекций так, чтобы она была расположена перед зрителем. Такую плоскость называют фронтальной (от фр. frontal, что означает «обращенный лицом к зрителю»). Обозначим ее буквой П с индексом два — П₂. Будем теперь строить проекцию предмета на эту плоскость, рассматривая предмет спереди. Для этого мысленно через характерные точки предмета, например вершины А, В, С и др., и точки отверстия проведем проецирующие лучи, перпендикулярные плоскости проекций П₂. Отметим точки A”, B”, C” пересечения их с плоскостью П₂ и соединим прямыми, а точки окружности – кривой линией. Мы получим проекцию предмета на плоскости П₂ (рис. 31, б).

Заметьте, что предмет был расположен перед плоскостью проекций так, что две его поверхности – передняя и задняя – оказались параллельными этой плоскости и спроецировались на нее без искажения. Другие поверхности, например перпендикулярные к плоскости проекций, изобразились в виде линий.

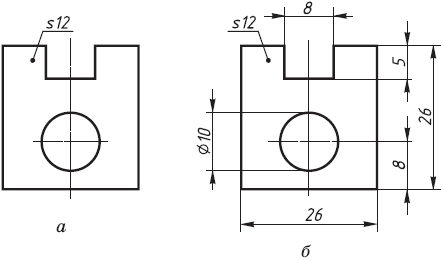
По полученной проекции мы сможем судить лишь о двух измерениях предмета – высоте и ширине, о диаметре отверстия, других элементах. А какова толщина предмета? Пользуясь полученной проекцией, мы этого сказать не можем. Значит, одна проекция не выявляет третьего измерения предмета. Чтобы по такому изображению можно было полностью судить о величине детали, его дополняют указанием толщины (s) детали (рис. 32, а). Так поступают, если предмет имеет простую форму, не содержит выступов, впадин и пр., т. е. его условно можно назвать «плоским».

Проставив другие размеры, мы будем иметь чертеж предмета, содержащий одну прямоугольную проекцию (рис. 32, б). Границы плоскости проекций при этом не показывают.

Проекции, на которых высоты различных частей объекта указаны числом, называют проекциями с числовыми отметками. С ними вы уже встречались на уроках «Человек и мир» и «География».

1. Какую плоскость проекций называют фронтальной? Как ее обозначают?
2. Для чего используются проекции с числовыми отметками?

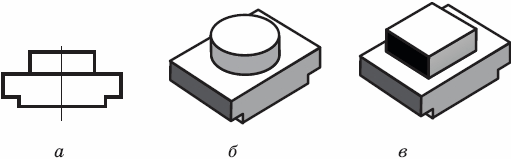
8.2. Прямоугольное проецирование на две плоскости проекций. Одна проекция не всегда однозначно определяет геометрическую форму предмета. Например, по одной проекции, данной на рисунке 33, а, можно представить предметы такими, как они показаны на рисунке 33, б и в. Можно мысленно подобрать и другие предметы, которые также будут иметь своей проекцией изображение, данное на рисунке 33, а. Кроме того, на таком изображении не отражено третье измерение предмета.

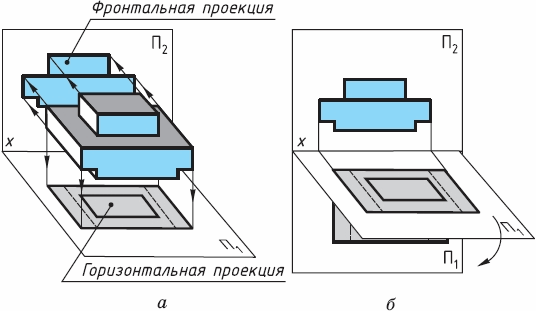
Все эти недостатки можно устранить, если построить не одну, а две прямоугольные проекции предмета на две взаимно перпендикулярные плоскости (рис. 34, а): фронтальную П₂ и горизонтальную П₁.

Чтобы получить проекцию на фронтальной плоскости П₂, предмет рассматривают спереди, а на горизонтальной плоскости П₁, – сверху. Проекцию на плоскости П₂ называют фронтальной, на плоскости П₁ – горизонтальной. Линию пересечения этих плоскостей (она обозначена х) называют осью проекций.

Построенные проекции оказались расположенными в пространстве в разных плоскостях (горизонтальной и вертикальной). Изображения же предмета обычно выполняют на одном листе, т. е. в одной плоскости. Поэтому для получения чертежа предмета обе плоскости совмещают в одну (рис. 34, б). Для этого поворачивают горизонтальную плоскость проекций вокруг оси х вниз на 90° так, чтобы она совпала с вертикальной плоскостью. Обе проекции окажутся расположенными в одной плоскости (рис. 35).

На совмещенных плоскостях фронтальная и горизонтальная проекции предмета располагаются в проекционной связи, т. е. горизонтальная проекция будет находиться точно под фронтальной (рис. 35, а). Прямая, которая соединяет (т. е. связывает) на чертеже две проекции одной и той же точки, называется линией связи. Так, фронтальные и горизонтальные проекции точек связаны вертикальными линиями связи. На рисунке 35, а такие линии для примера приведены только для точек крайних граней предмета.

Границы плоскостей проекций на чертеже можно не показывать, не наносят также и проекции проецирующих лучей и линию пересечения плоскостей проекций, т. е. ось проекций (рис. 35, б), если в этом нет необходимости.

Этот рисунок иллюстрирует одновременно и порядок расположения фронтальной и горизонтальной проекций.

Обратите внимание, что нижний выступ предмета оказался невидимым на горизонтальной проекции, поэтому он показан штриховыми линиями.

Способ прямоугольного проецирования на две взаимно перпендикулярные плоскости был разработан французским ученым-геометром Гаспаром Монжем в конце XVIII в. Поэтому такой способ часто называют методом Монжа.

Г. Монж положил начало развитию науки об изображении предметов – начертательной геометрии. Начертательная геометрия является теоретической основой черчения.

1. Всегда ли достаточно на чертеже одной проекции предмета?
2. Как называются плоскости проекций П₁ и П₂?
3. Как называются проекции, полученные при проецировании предмета на две плоскости проекций? Как должны располагаться эти плоскости относительно друг друга?

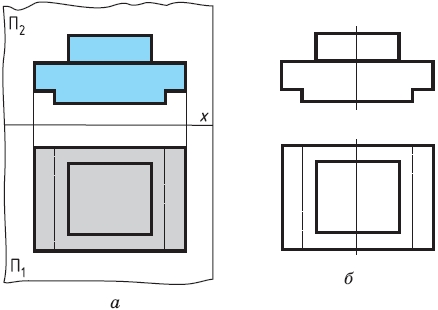
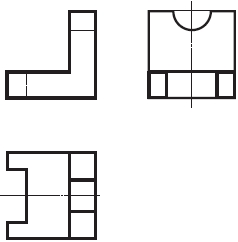
8.3. Прямоугольное проецирование на три плоскости проекций. Рассмотрим еще один пример. По чертежу на рисунке 36, а мы легко представим общую форму детали. Но форма выемки в вертикальной части остается невыявленной (рис. 36, б). Чтобы увидеть форму выемки, надо построить проекцию еще на одну плоскость. Ее располагают перпендикулярно плоскостям проекций П₁ и П₂ (рис. 37, а) и обозначают буквой П₃.

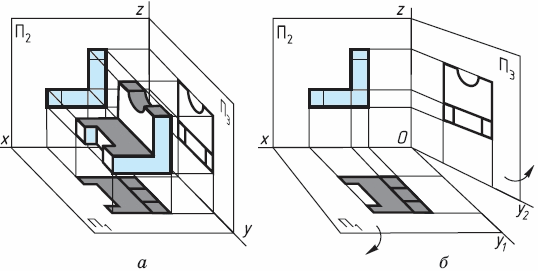
Третью плоскость проекций называют профильной, а полученную на ней проекцию — профильной проекцией предмета (от фр. profil, что означает «вид сбоку»). Проецируемый предмет помещают в пространстве трехгранного угла, образованного плоскостями П₁, П₂ и П₃, и рассматривают с трех сторон – спереди, сверху и слева. Через характерные точки предмета проводят проецирующие лучи до пересечения с плоскостями проекций. Точки пересечения соединяют прямыми или кривыми линиями. Полученные фигуры будут проекциями предмета на плоскостях П₁, П₂ и П₃.

Профильная плоскость проекций – вертикальная. Она перпендикулярна одновременно горизонтальной и фронтальной плоскостям проекций. В пересечении с плоскостью П₁ она образует ось у, а с плоскостью П₂ – ось z.

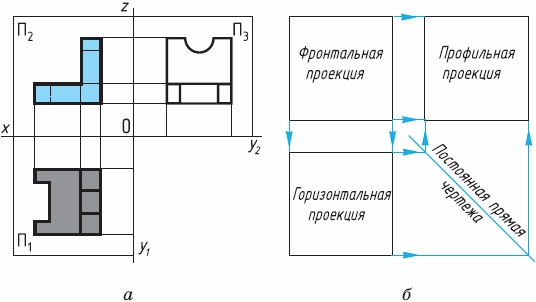
Для получения чертежа предмета плоскость П₃ поворачивают на 90° вправо, а плоскость П₁ – на 90° вниз (рис. 37, б). Полученный таким образом чертеж содержит три прямоугольные проекции предмета: фронтальную, горизонтальную и профильную (рис. 38, а). Линии связи на рисунке 38, а показаны только для точек, лежащих на крайних гранях предмета.

На рисунке 38, б приведена упрощенная схема расположения трех проекций на чертеже. Из нее видно, что профильную проекцию располагают в проекционной связи с фронтальной проекцией справа от нее. Линии, связывающие одни и те же точки фронтальной и профильной проекций, т. е. линии связи этих проекций, – горизонтальные.

При проведении линий связи между горизонтальной и профильной проекциями используют прямую, расположенную под углом 45° к любой вертикальной или горизонтальной линии на чертеже или рамке чертежа. Ее называют постоянной прямой чертежа.

Рисунок 39 содержит чертеж изображаемого нами предмета. Чертеж состоит из трех построенных проекций. Оси проекций и линии связи на чертеже не показаны.

Чертеж, состоящий из нескольких прямоугольных проекций, называют чертежом в системе прямоугольных проекций. Иногда такой чертеж называют комплексным. В зависимости от сложности геометрической формы предмета на чертеже он может быть представлен одной, двумя и более проекциями. Для краткости чертеж в системе прямоугольных проекций будем называть просто чертежом.

1. Какую проекцию называют фронтальной?
2. Как называют чертеж, состоящий из нескольких прямоугольных проекций?

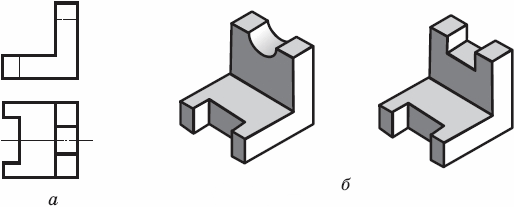
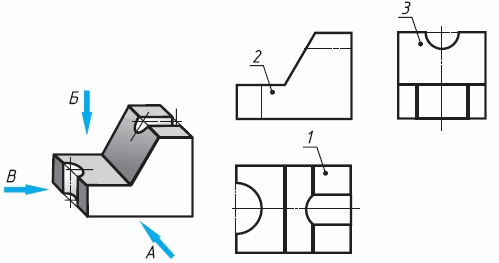
Ha рисунке 40 дано наглядное изображение и комплексный чертеж детали – угольника. На наглядном изображении стрелками показаны направления проецирования. Проекции детали обозначены цифрами: 1, 2, 3. Вам надо, не перечерчивая чертеж, записать в рабочей тетради:

1. какой проекции (обозначенной цифрой) соответствует каждое направление проецирования (обозначенное буквой);
2. названия проекций 1, 2 и 3.

Чертеж из трех проекций

Последняя бука буква “р”

Ответ на вопрос “Чертеж из трех проекций “, 4 буквы:
эпюр

Альтернативные вопросы в кроссвордах для слова эпюр

Вид чертежа 4 буквы

Чертёж, на котором пространственная фигура изображена методом ортогональных проекций на три плоскости

Чертеж из трех проекций, взаимно перпендикулярных

Чертеж из 3 проекций, взаимно перпендик

Чертежная рифма к гипюру

Двукартинный чертеж пространственной фигуры

Определение слова эпюр в словарях

Википедия Значение слова в словаре Википедия
Эпюр — многозначный термин: Эпюр — схематический чертёж или график в начертательной геометрии . Эпюра — особый вид графиков, показывающий распределение величины нагрузки на объект. Расчет эпюр напряжения является базовой задачей такой дисциплины, как сопротивление.

Энциклопедический словарь, 1998 г. Значение слова в словаре Энциклопедический словарь, 1998 г.
ЭПЮР (эпюра) (от франц. epure – чертеж) чертеж, на котором пространственная фигура изображена методом двух (или трех) ортогональных проекций на взаимно перпендикулярные, а затем развернутые плоскости.

Примеры употребления слова эпюр в литературе.

Инженер Фолстен, человек малообщительный, он либо погружен в цифры, либо чертит эпюры машин с планом, разрезами и видом снизу.

Тихо жужжали лампы дневного света в чертежных залах общежития, где мы делали семестровый эпюр.

Источник: библиотека Максима Мошкова

Чертеж из 3 проекций

В зависимости от положения относительно плоскостей проекций различают плоскости общего положения и плоскости частного положения.

Плоскость общего положения – плоскость, наклоненная под произвольными углами к плоскостям проекций (рис.1).

Плоскости частного положения можно разделить на две группы – проецирующие плоскости и плоскости уровня. Плоскости частного положения чаще всего задаются следами.

Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня. Все объекты, лежащие в плоскости уровня, проецируются на параллельную плоскость проекций в натуральную величину.

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (рис.2).

Треугольник ABC, лежащий в горизонтальной плоскости уровня, проецируется на П1 в натуральную величину.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (рис. 3).

Треугольник ABC, лежащий во фронтальной плоскости уровня, проецируется на П2 в натуральную величину.

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (рис. 4).

Треугольник ABC, лежащий в профильной плоскости уровня, проецируется на плоскость П3 в натуральную величину.

Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими.

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций П1 (рис.5).

Горизонтально-проецирующая плоскость задается горизонтальным следом плоскости ∑1

Углы наклона горизонтально-проецирующей плоскости к П2 и П3 проецируются на горизонтальную плоскость проекций в натуральную величину.

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций П2, задается фронтальным следом плоскости ∆2 (рис.6).

Проекции всех линий и точек, лежащих во фронтально-проецирующей плоскости, совпадают с фронтальным следом этой плоскости. Углы наклона фронтально-проецирующей плоскости к П1 и П3 проецируются на фронтальную плоскость проекций в натуральную величину.

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций П3 , задается профильным следом плоскости Г3 (рис. 7).